Generating extreme quantum scattering in graphene with machine learning

Graphene quantum dots provide a platform for manipulating electron behaviors in two-dimensional (2D) Dirac materials. Most previous works were of the "forward" type in that the objective was to solve various confinement, transport and scattering problems with given structures that can be generated by, e.g., applying an external electrical field. There are applications such as cloaking or superscattering where the challenging problem of inverse design needs to be solved: finding a quantum-dot structure according to certain desired functional characteristics. A brute-force search of the system configuration based directly on the solutions of the Dirac equation is computational infeasible. We articulate a machine-learning approach to addressing the inverse-design problem where artificial neural networks subject to physical constraints are exploited to replace the rigorous Dirac equation solver. In particular, we focus on the problem of designing a quantum dot structure to generate both cloaking and superscattering in terms of the scattering efficiency as a function of the energy. We construct a physical loss function that enables accurate prediction of the scattering characteristics. We demonstrate that, in the regime of Klein tunneling, the scattering efficiency can be designed to vary over two orders of magnitudes, allowing any scattering curve to be generated from a proper combination of the gate potentials. Our physics-based machine-learning approach can be a powerful design tool for 2D Dirac material-based electronics.

Tomography of time-dependent quantum spin networks with machine learning

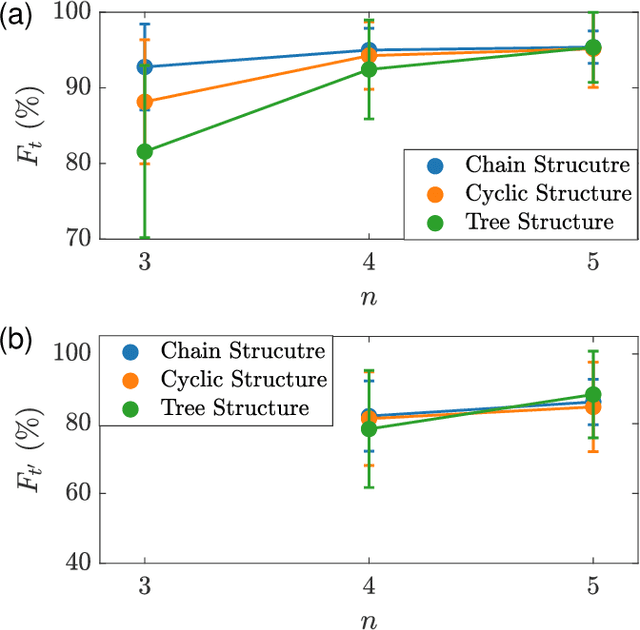
Interacting spin networks are fundamental to quantum computing. Data-based tomography of time-independent spin networks has been achieved, but an open challenge is to ascertain the structures of time-dependent spin networks using time series measurements taken locally from a small subset of the spins. Physically, the dynamical evolution of a spin network under time-dependent driving or perturbation is described by the Heisenberg equation of motion. Motivated by this basic fact, we articulate a physics-enhanced machine learning framework whose core is Heisenberg neural networks. In particular, we develop a deep learning algorithm according to some physics motivated loss function based on the Heisenberg equation, which "forces" the neural network to follow the quantum evolution of the spin variables. We demonstrate that, from local measurements, not only the local Hamiltonian can be recovered but the Hamiltonian reflecting the interacting structure of the whole system can also be faithfully reconstructed. We test our Heisenberg neural machine on spin networks of a variety of structures. In the extreme case where measurements are taken from only one spin, the achieved tomography fidelity values can reach about 90%. The developed machine learning framework is applicable to any time-dependent systems whose quantum dynamical evolution is governed by the Heisenberg equation of motion.

Adaptable Hamiltonian neural networks

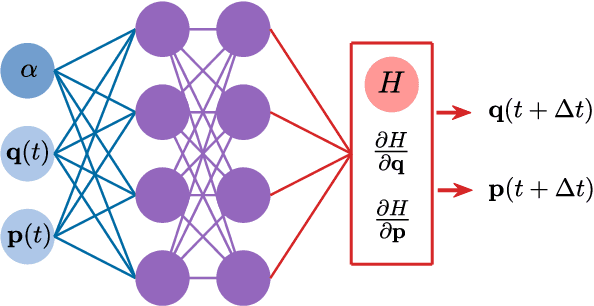
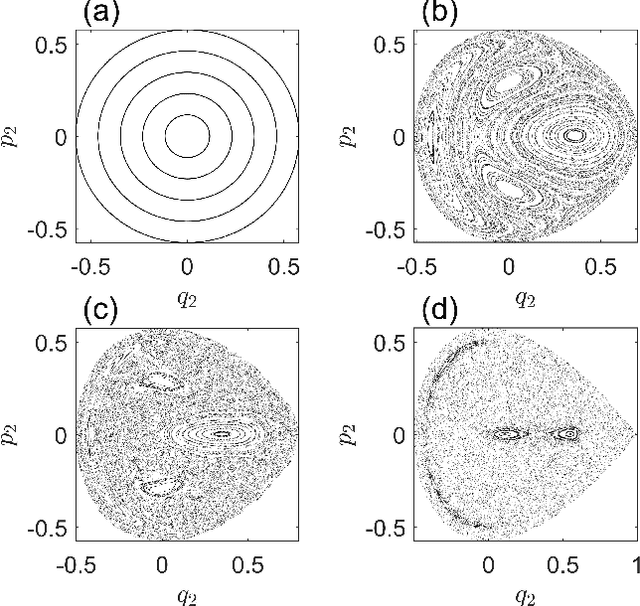
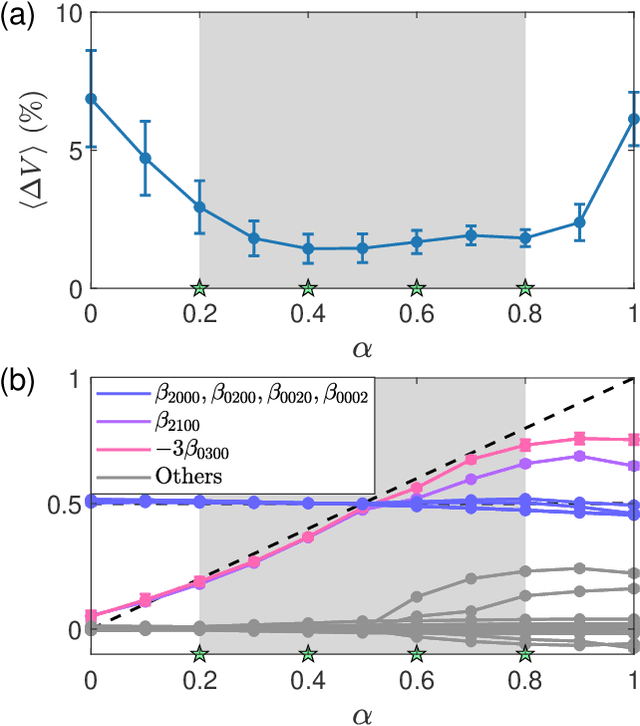
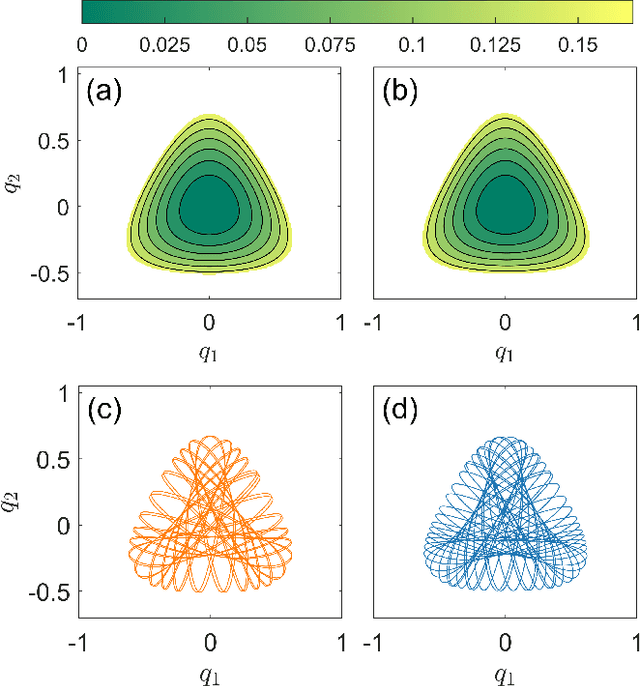
The rapid growth of research in exploiting machine learning to predict chaotic systems has revived a recent interest in Hamiltonian Neural Networks (HNNs) with physical constraints defined by the Hamilton's equations of motion, which represent a major class of physics-enhanced neural networks. We introduce a class of HNNs capable of adaptable prediction of nonlinear physical systems: by training the neural network based on time series from a small number of bifurcation-parameter values of the target Hamiltonian system, the HNN can predict the dynamical states at other parameter values, where the network has not been exposed to any information about the system at these parameter values. The architecture of the HNN differs from the previous ones in that we incorporate an input parameter channel, rendering the HNN parameter--cognizant. We demonstrate, using paradigmatic Hamiltonian systems, that training the HNN using time series from as few as four parameter values bestows the neural machine with the ability to predict the state of the target system in an entire parameter interval. Utilizing the ensemble maximum Lyapunov exponent and the alignment index as indicators, we show that our parameter-cognizant HNN can successfully predict the route of transition to chaos. Physics-enhanced machine learning is a forefront area of research, and our adaptable HNNs provide an approach to understanding machine learning with broad applications.