Machine-learning prediction of tipping and collapse of the Atlantic Meridional Overturning Circulation

Recent research on the Atlantic Meridional Overturning Circulation (AMOC) raised concern about its potential collapse through a tipping point due to the climate-change caused increase in the freshwater input into the North Atlantic. The predicted time window of collapse is centered about the middle of the century and the earliest possible start is approximately two years from now. More generally, anticipating a tipping point at which the system transitions from one stable steady state to another is relevant to a broad range of fields. We develop a machine-learning approach to predicting tipping in noisy dynamical systems with a time-varying parameter and test it on a number of systems including the AMOC, ecological networks, an electrical power system, and a climate model. For the AMOC, our prediction based on simulated fingerprint data and real data of the sea surface temperature places the time window of a potential collapse between the years 2040 and 2065.

Model-free tracking control of complex dynamical trajectories with machine learning

Nonlinear tracking control enabling a dynamical system to track a desired trajectory is fundamental to robotics, serving a wide range of civil and defense applications. In control engineering, designing tracking control requires complete knowledge of the system model and equations. We develop a model-free, machine-learning framework to control a two-arm robotic manipulator using only partially observed states, where the controller is realized by reservoir computing. Stochastic input is exploited for training, which consists of the observed partial state vector as the first and its immediate future as the second component so that the neural machine regards the latter as the future state of the former. In the testing (deployment) phase, the immediate-future component is replaced by the desired observational vector from the reference trajectory. We demonstrate the effectiveness of the control framework using a variety of periodic and chaotic signals, and establish its robustness against measurement noise, disturbances, and uncertainties.

Emergence of a stochastic resonance in machine learning

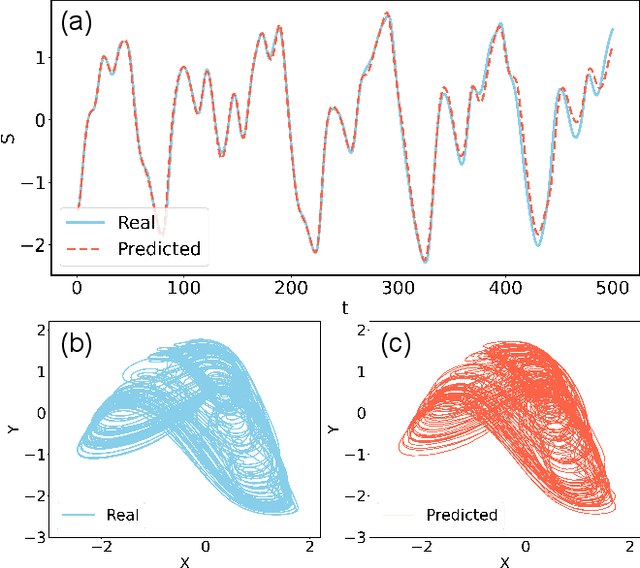
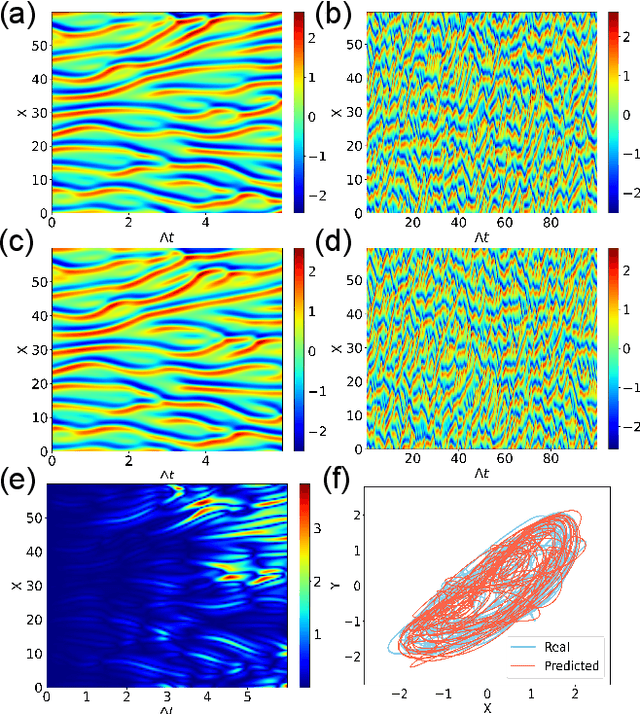
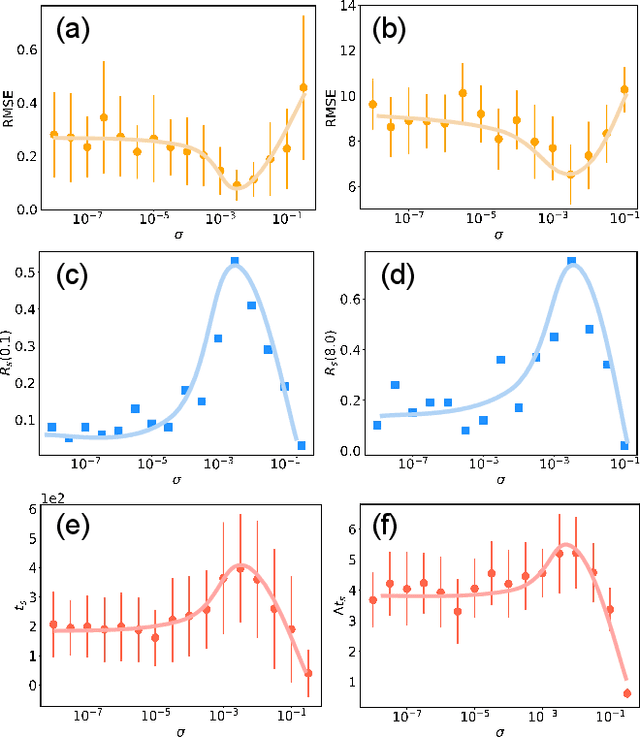
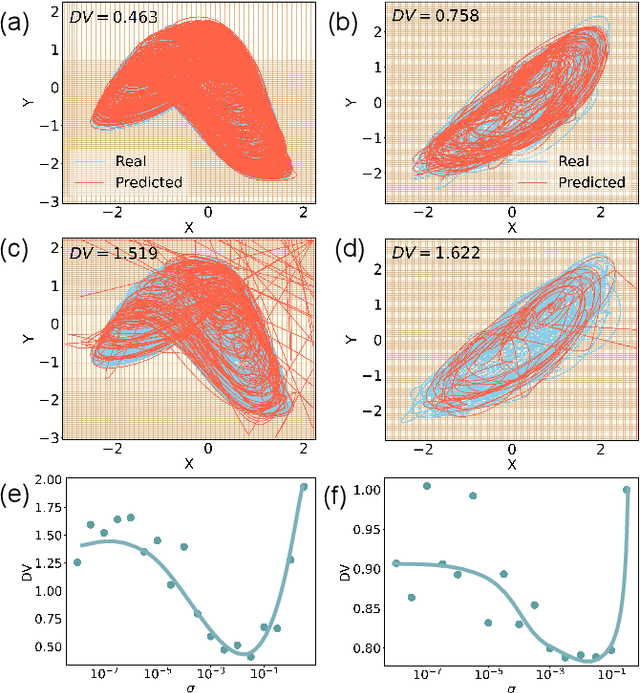
Can noise be beneficial to machine-learning prediction of chaotic systems? Utilizing reservoir computers as a paradigm, we find that injecting noise to the training data can induce a stochastic resonance with significant benefits to both short-term prediction of the state variables and long-term prediction of the attractor of the system. A key to inducing the stochastic resonance is to include the amplitude of the noise in the set of hyperparameters for optimization. By so doing, the prediction accuracy, stability and horizon can be dramatically improved. The stochastic resonance phenomenon is demonstrated using two prototypical high-dimensional chaotic systems.

Digital twins of nonlinear dynamical systems

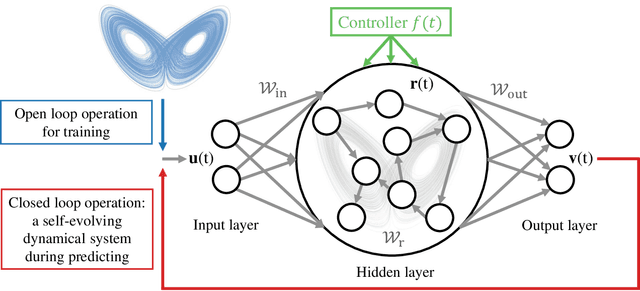
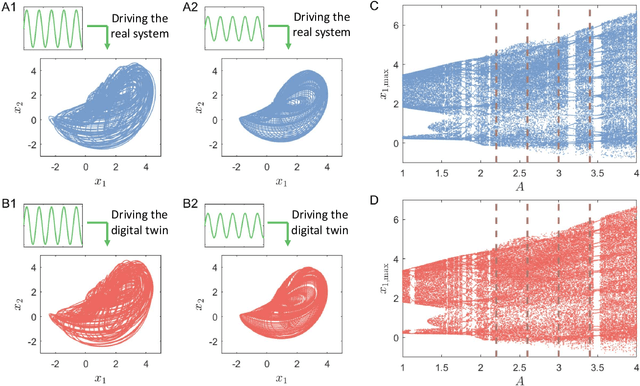
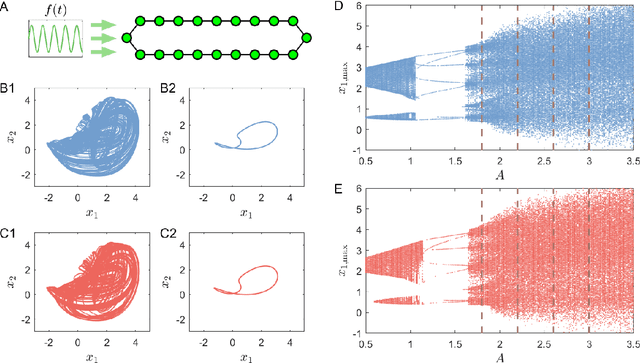
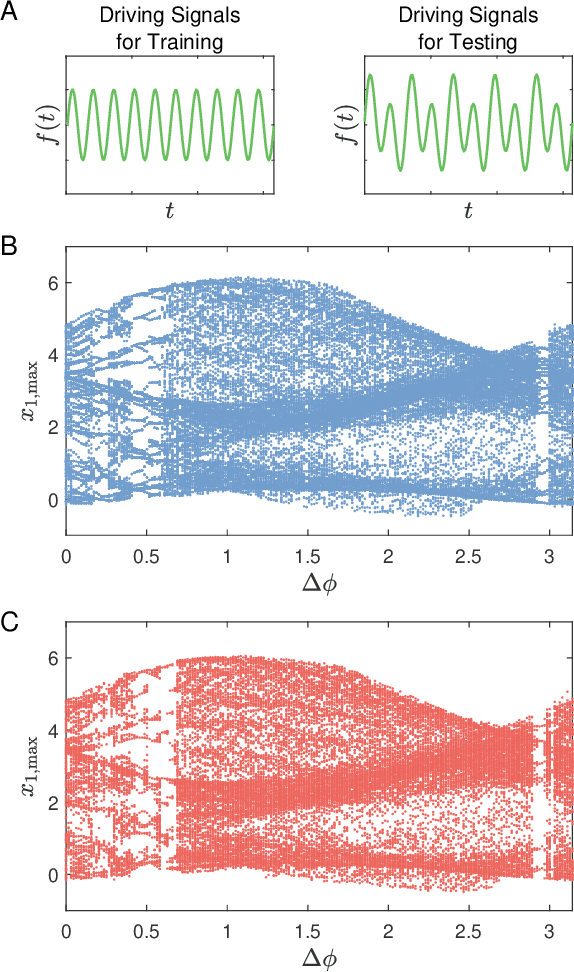
We articulate the design imperatives for machine-learning based digital twins for nonlinear dynamical systems subject to external driving, which can be used to monitor the ``health'' of the target system and anticipate its future collapse. We demonstrate that, with single or parallel reservoir computing configurations, the digital twins are capable of challenging forecasting and monitoring tasks. Employing prototypical systems from climate, optics and ecology, we show that the digital twins can extrapolate the dynamics of the target system to certain parameter regimes never experienced before, make continual forecasting/monitoring with sparse real-time updates under non-stationary external driving, infer hidden variables and accurately predict their dynamical evolution, adapt to different forms of external driving, and extrapolate the global bifurcation behaviors to systems of some different sizes. These features make our digital twins appealing in significant applications such as monitoring the health of critical systems and forecasting their potential collapse induced by environmental changes.

Anticipating synchronization with machine learning

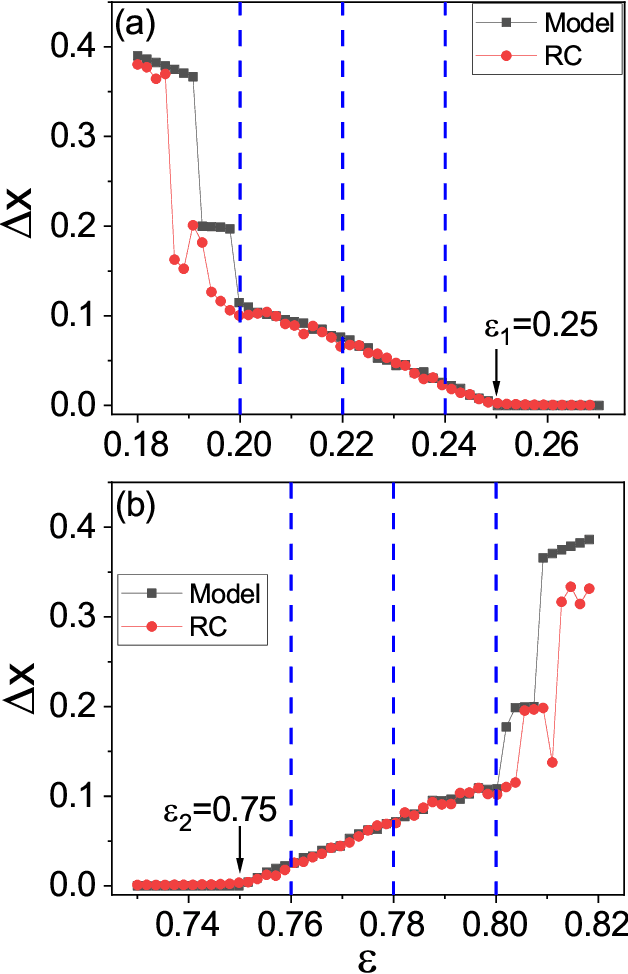
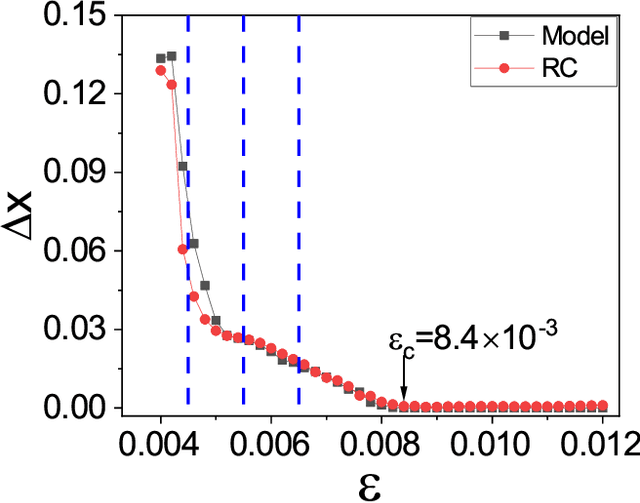
In applications of dynamical systems, situations can arise where it is desired to predict the onset of synchronization as it can lead to characteristic and significant changes in the system performance and behaviors, for better or worse. In experimental and real settings, the system equations are often unknown, raising the need to develop a prediction framework that is model free and fully data driven. We contemplate that this challenging problem can be addressed with machine learning. In particular, exploiting reservoir computing or echo state networks, we devise a "parameter-aware" scheme to train the neural machine using asynchronous time series, i.e., in the parameter regime prior to the onset of synchronization. A properly trained machine will possess the power to predict the synchronization transition in that, with a given amount of parameter drift, whether the system would remain asynchronous or exhibit synchronous dynamics can be accurately anticipated. We demonstrate the machine-learning based framework using representative chaotic models and small network systems that exhibit continuous (second-order) or abrupt (first-order) transitions. A remarkable feature is that, for a network system exhibiting an explosive (first-order) transition and a hysteresis loop in synchronization, the machine learning scheme is capable of accurately predicting these features, including the precise locations of the transition points associated with the forward and backward transition paths.

Machine learning prediction of critical transition and system collapse

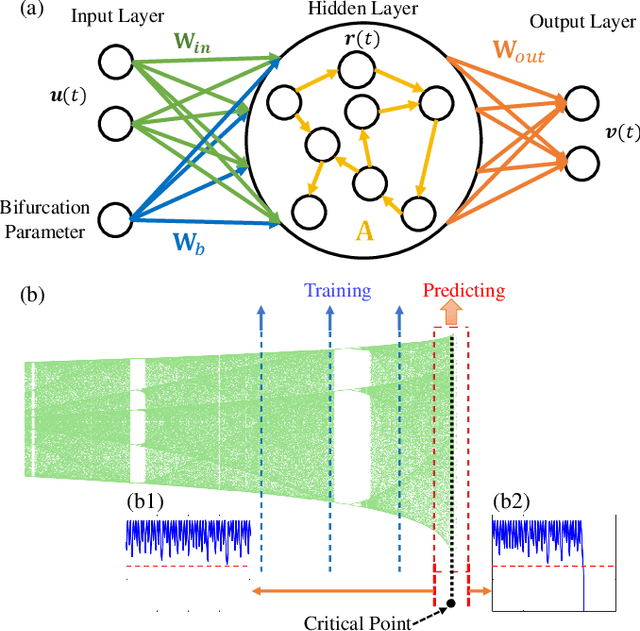
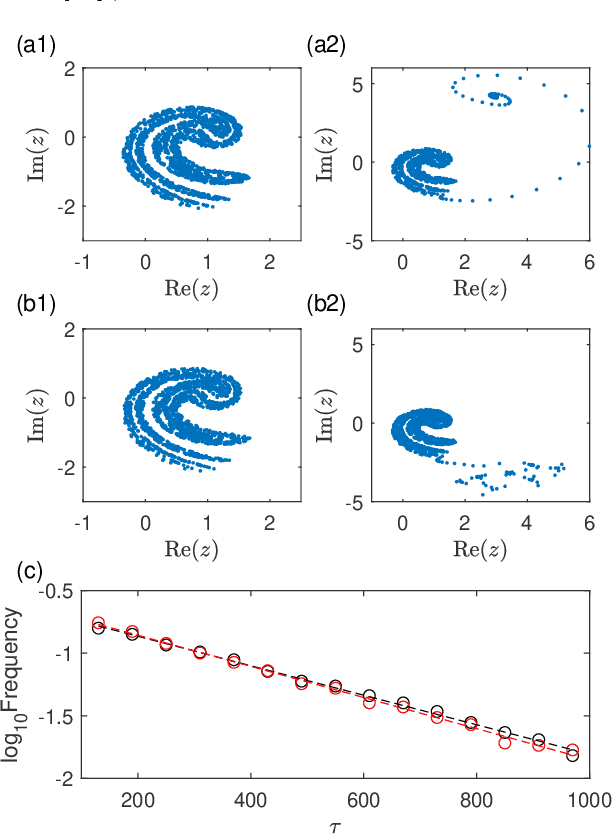
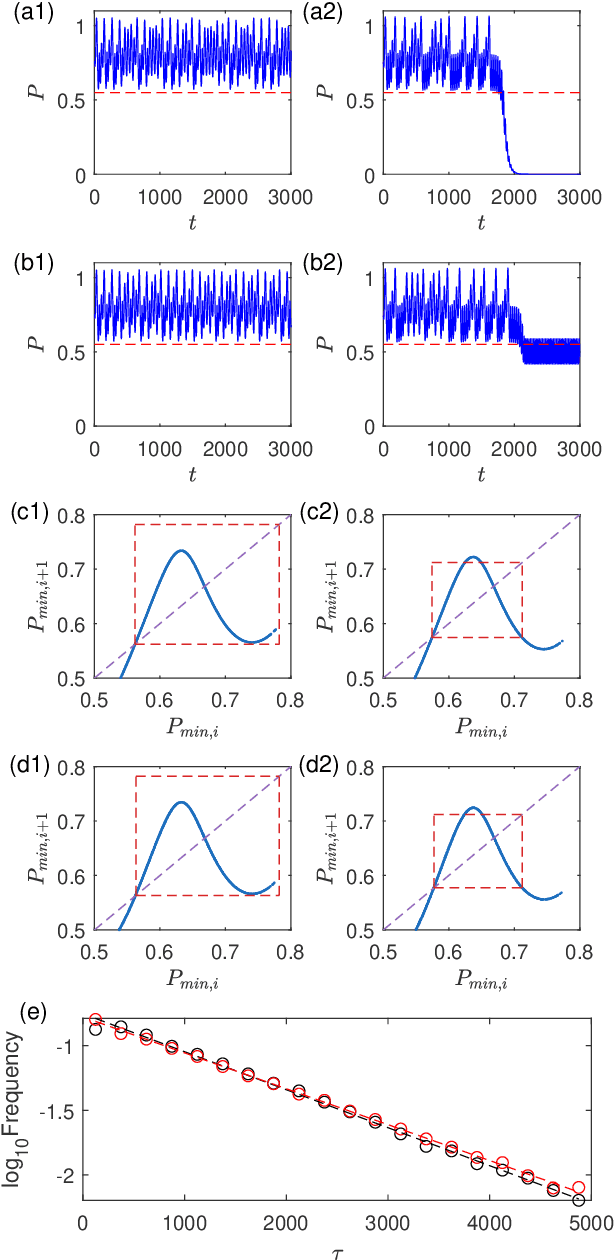
To predict a critical transition due to parameter drift without relying on model is an outstanding problem in nonlinear dynamics and applied fields. A closely related problem is to predict whether the system is already in or if the system will be in a transient state preceding its collapse. We develop a model free, machine learning based solution to both problems by exploiting reservoir computing to incorporate a parameter input channel. We demonstrate that, when the machine is trained in the normal functioning regime with a chaotic attractor (i.e., before the critical transition), the transition point can be predicted accurately. Remarkably, for a parameter drift through the critical point, the machine with the input parameter channel is able to predict not only that the system will be in a transient state, but also the average transient time before the final collapse.