Hua-Wei Fan
Machine learning prediction of critical transition and system collapse
Dec 02, 2020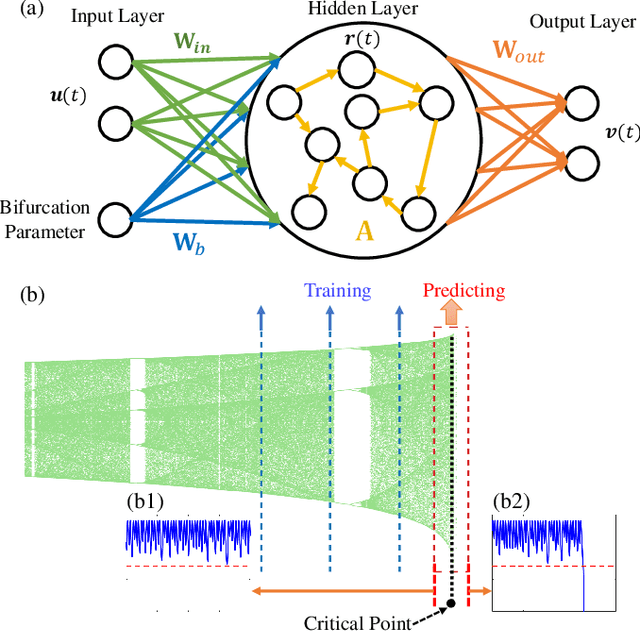
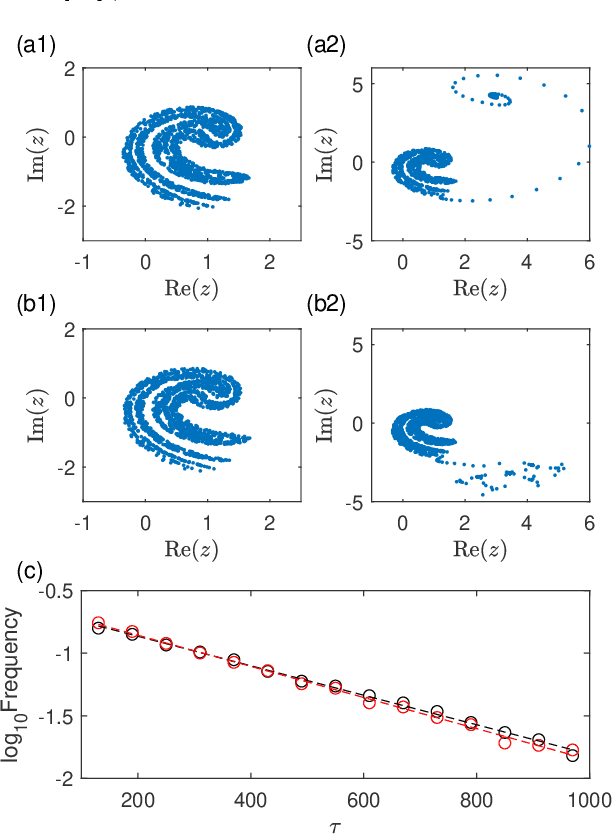
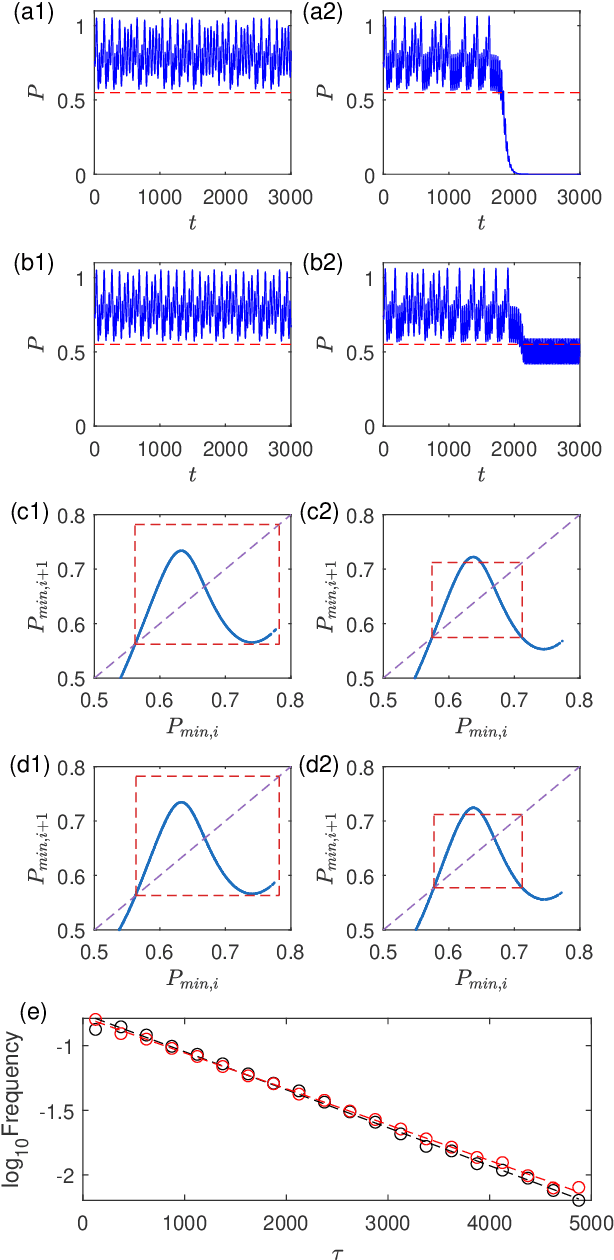
Abstract:To predict a critical transition due to parameter drift without relying on model is an outstanding problem in nonlinear dynamics and applied fields. A closely related problem is to predict whether the system is already in or if the system will be in a transient state preceding its collapse. We develop a model free, machine learning based solution to both problems by exploiting reservoir computing to incorporate a parameter input channel. We demonstrate that, when the machine is trained in the normal functioning regime with a chaotic attractor (i.e., before the critical transition), the transition point can be predicted accurately. Remarkably, for a parameter drift through the critical point, the machine with the input parameter channel is able to predict not only that the system will be in a transient state, but also the average transient time before the final collapse.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge