Predicting extreme events from data using deep machine learning: when and where

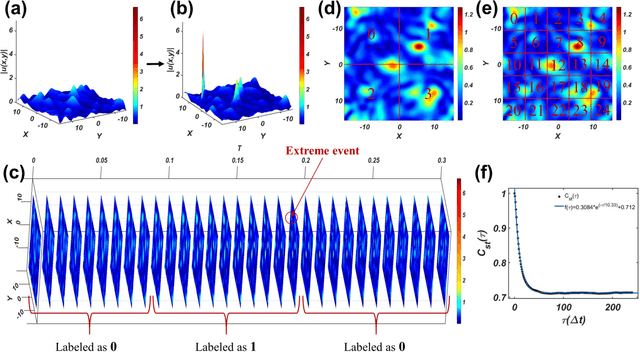
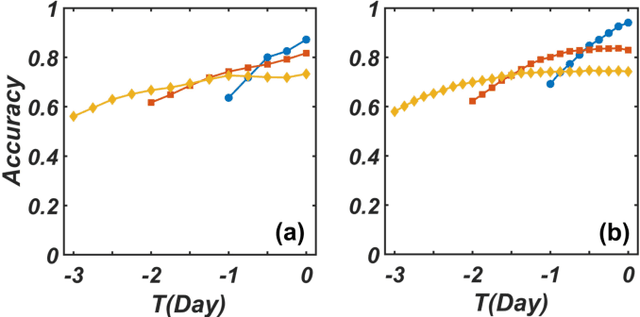
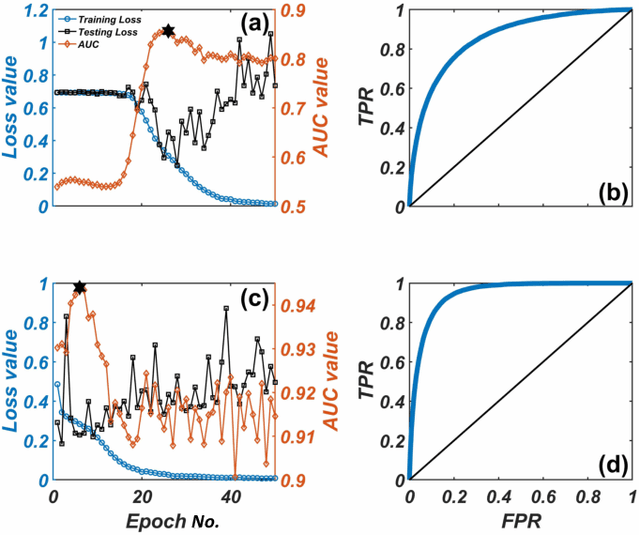
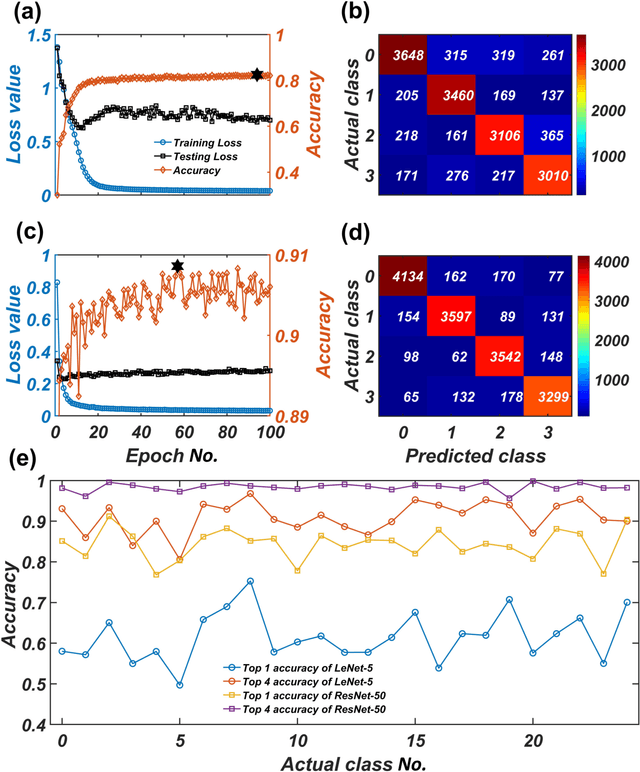
We develop a deep convolutional neural network (DCNN) based framework for model-free prediction of the occurrence of extreme events both in time ("when") and in space ("where") in nonlinear physical systems of spatial dimension two. The measurements or data are a set of two-dimensional snapshots or images. For a desired time horizon of prediction, a proper labeling scheme can be designated to enable successful training of the DCNN and subsequent prediction of extreme events in time. Given that an extreme event has been predicted to occur within the time horizon, a space-based labeling scheme can be applied to predict, within certain resolution, the location at which the event will occur. We use synthetic data from the 2D complex Ginzburg-Landau equation and empirical wind speed data of the North Atlantic ocean to demonstrate and validate our machine-learning based prediction framework. The trade-offs among the prediction horizon, spatial resolution, and accuracy are illustrated, and the detrimental effect of spatially biased occurrence of extreme event on prediction accuracy is discussed. The deep learning framework is viable for predicting extreme events in the real world.

Machine learning prediction of critical transition and system collapse

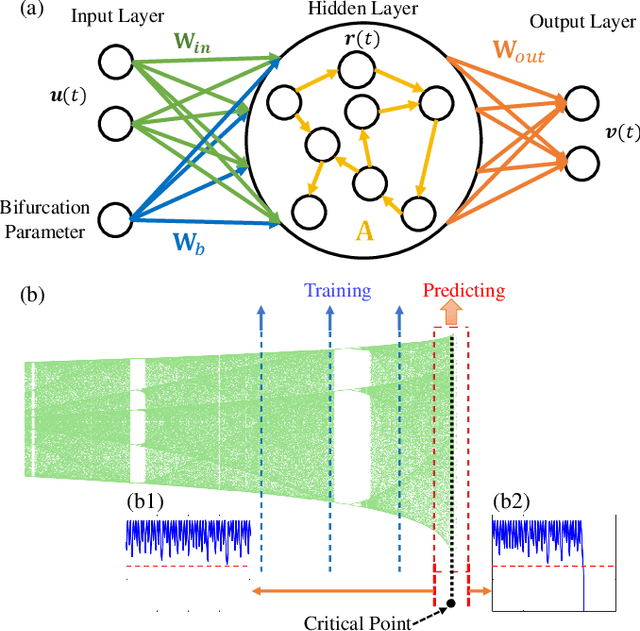
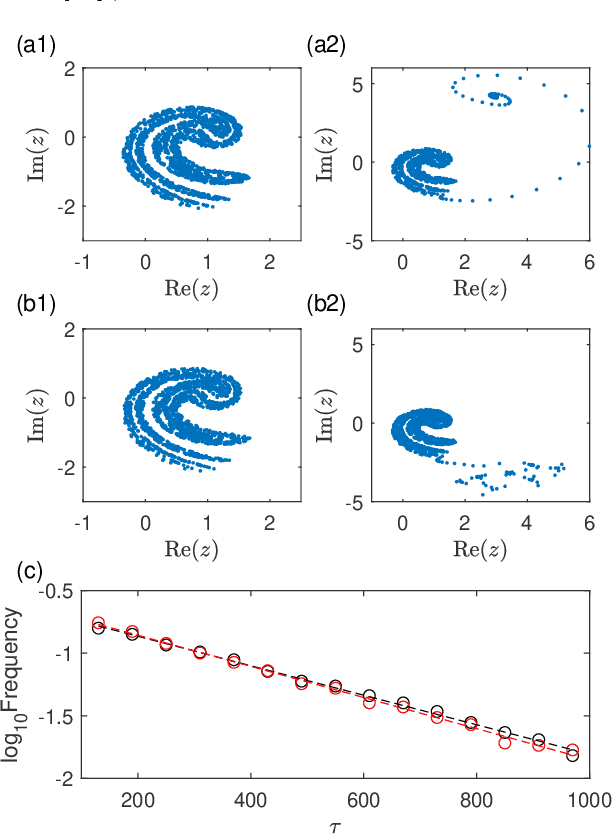
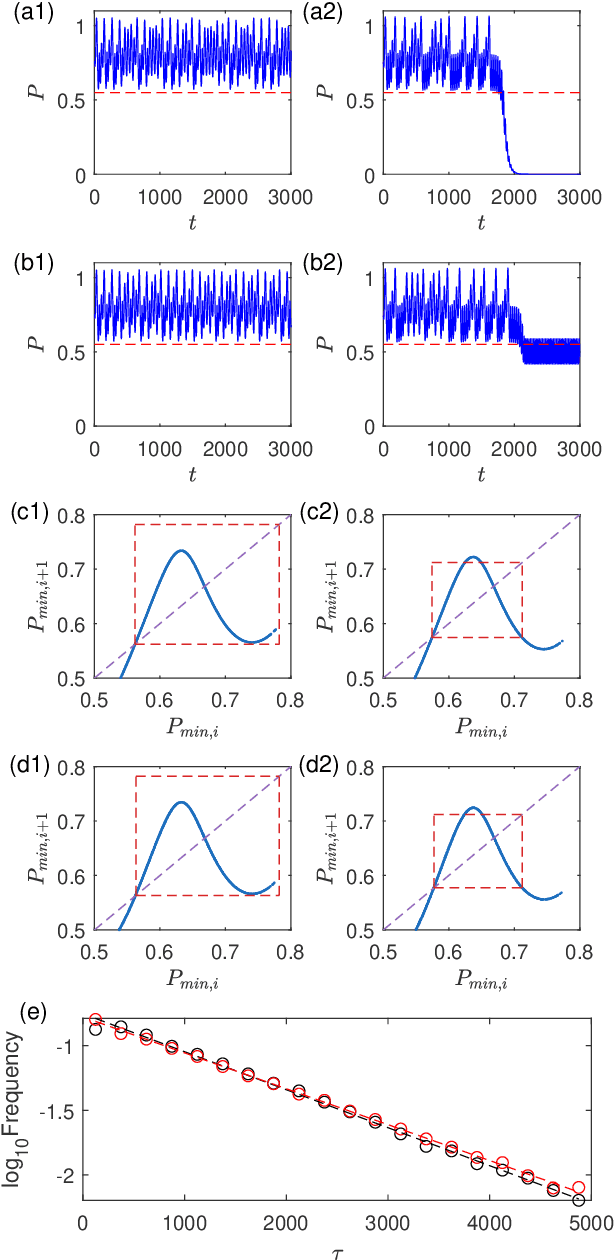
To predict a critical transition due to parameter drift without relying on model is an outstanding problem in nonlinear dynamics and applied fields. A closely related problem is to predict whether the system is already in or if the system will be in a transient state preceding its collapse. We develop a model free, machine learning based solution to both problems by exploiting reservoir computing to incorporate a parameter input channel. We demonstrate that, when the machine is trained in the normal functioning regime with a chaotic attractor (i.e., before the critical transition), the transition point can be predicted accurately. Remarkably, for a parameter drift through the critical point, the machine with the input parameter channel is able to predict not only that the system will be in a transient state, but also the average transient time before the final collapse.