Inferring Attracting Basins of Power System with Machine Learning

Power systems dominated by renewable energy encounter frequently large, random disturbances, and a critical challenge faced in power-system management is how to anticipate accurately whether the perturbed systems will return to the functional state after the transient or collapse. Whereas model-based studies show that the key to addressing the challenge lies in the attracting basins of the functional and dysfunctional states in the phase space, the finding of the attracting basins for realistic power systems remains a challenge, as accurate models describing the system dynamics are generally unavailable. Here we propose a new machine learning technique, namely balanced reservoir computing, to infer the attracting basins of a typical power system based on measured data. Specifically, trained by the time series of a handful of perturbation events, we demonstrate that the trained machine can predict accurately whether the system will return to the functional state in response to a large, random perturbation, thereby reconstructing the attracting basin of the functional state. The working mechanism of the new machine is analyzed, and it is revealed that the success of the new machine is attributed to the good balance between the echo and fading properties of the reservoir network; the effect of noisy signals on the prediction performance is also investigated, and a stochastic-resonance-like phenomenon is observed. Finally, we demonstrate that the new technique can be also utilized to infer the attracting basins of coexisting attractors in typical chaotic systems.

Learning Hamiltonian dynamics by reservoir computer

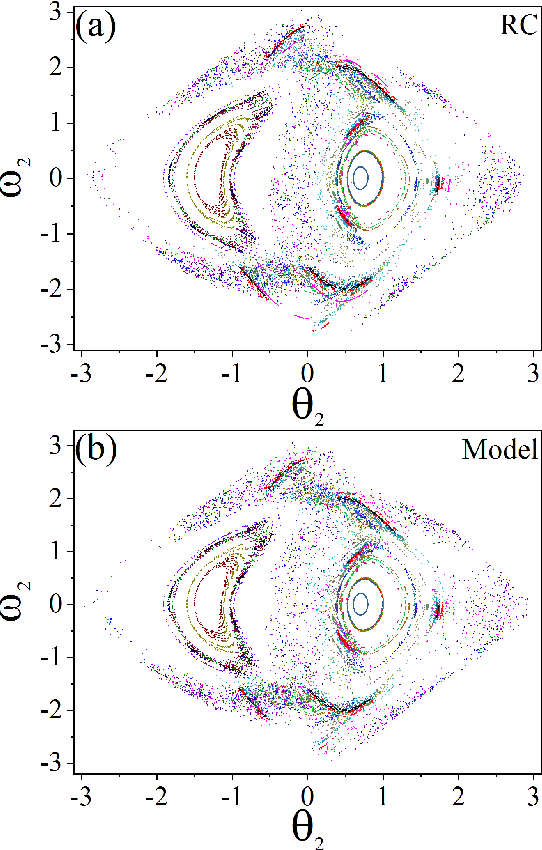
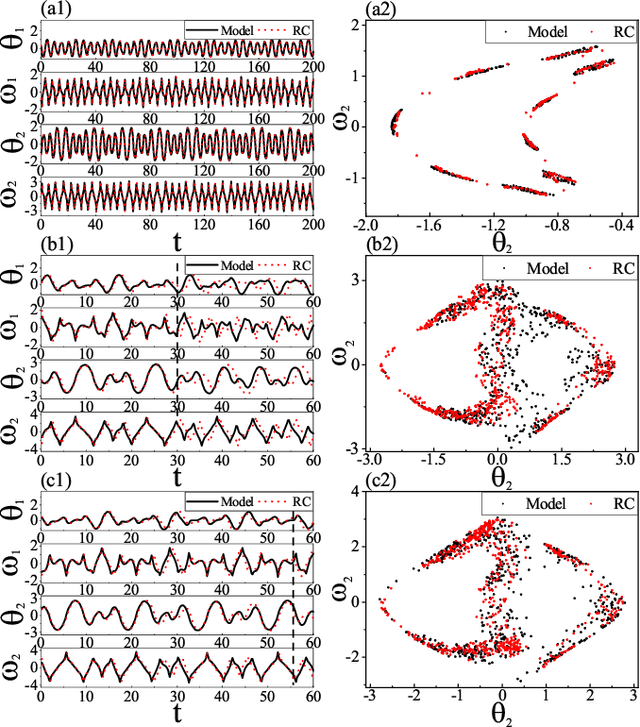
Reconstructing the KAM dynamics diagram of Hamiltonian system from the time series of a limited number of parameters is an outstanding question in nonlinear science, especially when the Hamiltonian governing the system dynamics are unknown. Here, we demonstrate that this question can be addressed by the machine learning approach knowing as reservoir computer (RC). Specifically, we show that without prior knowledge about the Hamilton's equations of motion, the trained RC is able to not only predict the short-term evolution of the system state, but also replicate the long-term ergodic properties of the system dynamics. Furthermore, by the architecture of parameter-aware RC, we also show that the RC trained by the time series acquired at a handful parameters is able to reconstruct the entire KAM dynamics diagram with a high precision by tuning a control parameter externally. The feasibility and efficiency of the learning techniques are demonstrated in two classical nonlinear Hamiltonian systems, namely the double-pendulum oscillator and the standard map. Our study indicates that, as a complex dynamical system, RC is able to learn from data the Hamiltonian.

Anticipating synchronization with machine learning

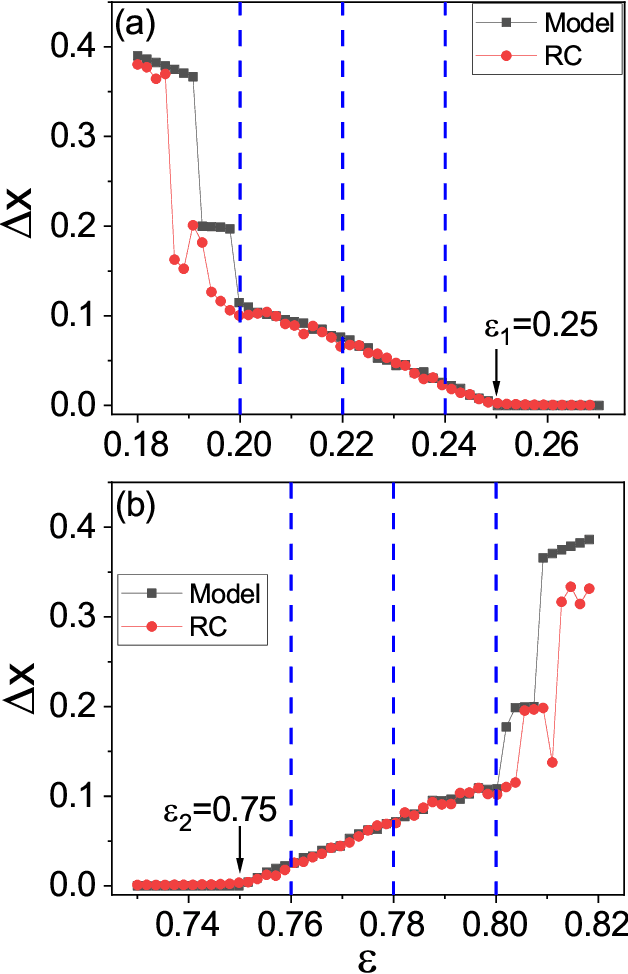
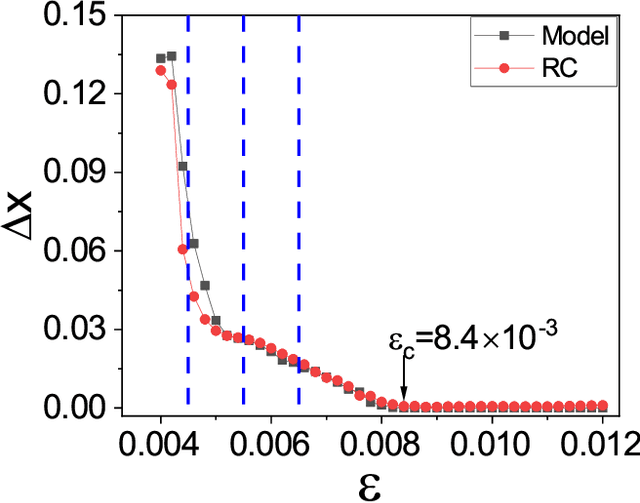
In applications of dynamical systems, situations can arise where it is desired to predict the onset of synchronization as it can lead to characteristic and significant changes in the system performance and behaviors, for better or worse. In experimental and real settings, the system equations are often unknown, raising the need to develop a prediction framework that is model free and fully data driven. We contemplate that this challenging problem can be addressed with machine learning. In particular, exploiting reservoir computing or echo state networks, we devise a "parameter-aware" scheme to train the neural machine using asynchronous time series, i.e., in the parameter regime prior to the onset of synchronization. A properly trained machine will possess the power to predict the synchronization transition in that, with a given amount of parameter drift, whether the system would remain asynchronous or exhibit synchronous dynamics can be accurately anticipated. We demonstrate the machine-learning based framework using representative chaotic models and small network systems that exhibit continuous (second-order) or abrupt (first-order) transitions. A remarkable feature is that, for a network system exhibiting an explosive (first-order) transition and a hysteresis loop in synchronization, the machine learning scheme is capable of accurately predicting these features, including the precise locations of the transition points associated with the forward and backward transition paths.

Transfer learning of chaotic systems

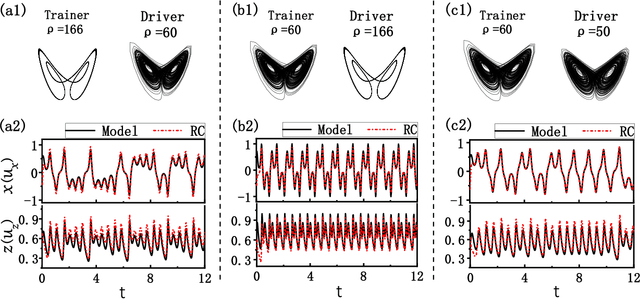
Can a neural network trained by the time series of system A be used to predict the evolution of system B? This problem, knowing as transfer learning in a broad sense, is of great importance in machine learning and data mining, yet has not been addressed for chaotic systems. Here we investigate transfer learning of chaotic systems from the perspective of synchronization-based state inference, in which a reservoir computer trained by chaotic system A is used to infer the unmeasured variables of chaotic system B, while A is different from B in either parameter or dynamics. It is found that if systems A and B are different in parameter, the reservoir computer can be well synchronized to system B. However, if systems A and B are different in dynamics, the reservoir computer fails to synchronize with system B in general. Knowledge transfer along a chain of coupled reservoir computers is also studied, and it is found that, although the reservoir computers are trained by different systems, the unmeasured variables of the driving system can be successfully inferred by the remote reservoir computer. Finally, by an experiment of chaotic pendulum, we show that the knowledge learned from the modeling system can be used to predict the evolution of the experimental system.

Long-term prediction of chaotic systems with recurrent neural networks

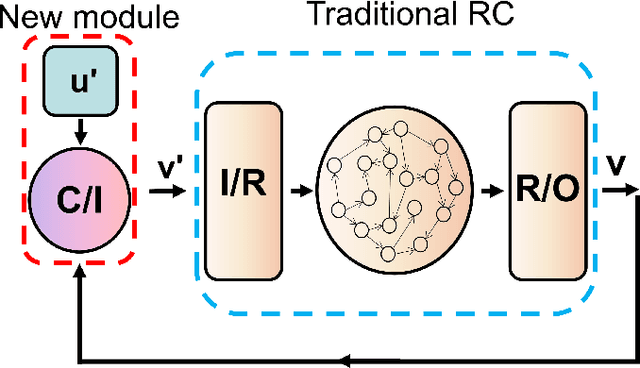
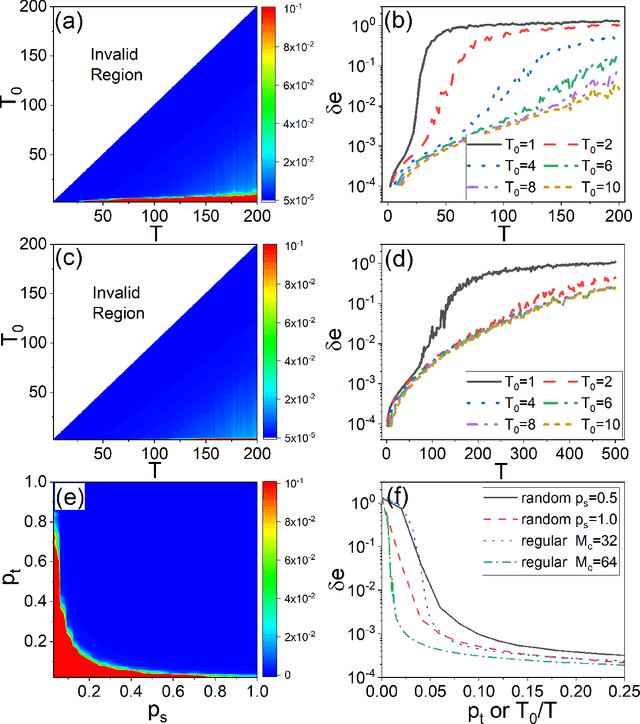
Reservoir computing systems, a class of recurrent neural networks, have recently been exploited for model-free, data-based prediction of the state evolution of a variety of chaotic dynamical systems. The prediction horizon demonstrated has been about half dozen Lyapunov time. Is it possible to significantly extend the prediction time beyond what has been achieved so far? We articulate a scheme incorporating time-dependent but sparse data inputs into reservoir computing and demonstrate that such rare "updates" of the actual state practically enable an arbitrarily long prediction horizon for a variety of chaotic systems. A physical understanding based on the theory of temporal synchronization is developed.