Transfer learning of chaotic systems
Paper and Code
Nov 15, 2020
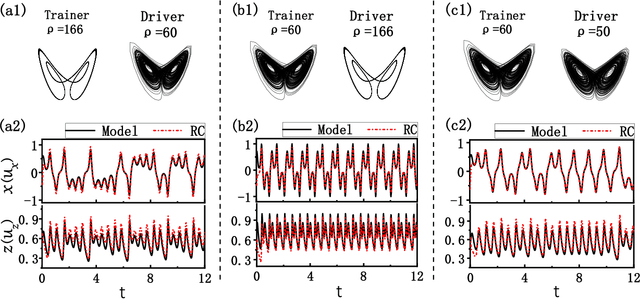


Can a neural network trained by the time series of system A be used to predict the evolution of system B? This problem, knowing as transfer learning in a broad sense, is of great importance in machine learning and data mining, yet has not been addressed for chaotic systems. Here we investigate transfer learning of chaotic systems from the perspective of synchronization-based state inference, in which a reservoir computer trained by chaotic system A is used to infer the unmeasured variables of chaotic system B, while A is different from B in either parameter or dynamics. It is found that if systems A and B are different in parameter, the reservoir computer can be well synchronized to system B. However, if systems A and B are different in dynamics, the reservoir computer fails to synchronize with system B in general. Knowledge transfer along a chain of coupled reservoir computers is also studied, and it is found that, although the reservoir computers are trained by different systems, the unmeasured variables of the driving system can be successfully inferred by the remote reservoir computer. Finally, by an experiment of chaotic pendulum, we show that the knowledge learned from the modeling system can be used to predict the evolution of the experimental system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge