Learning Hamiltonian dynamics by reservoir computer
Paper and Code
Apr 24, 2021
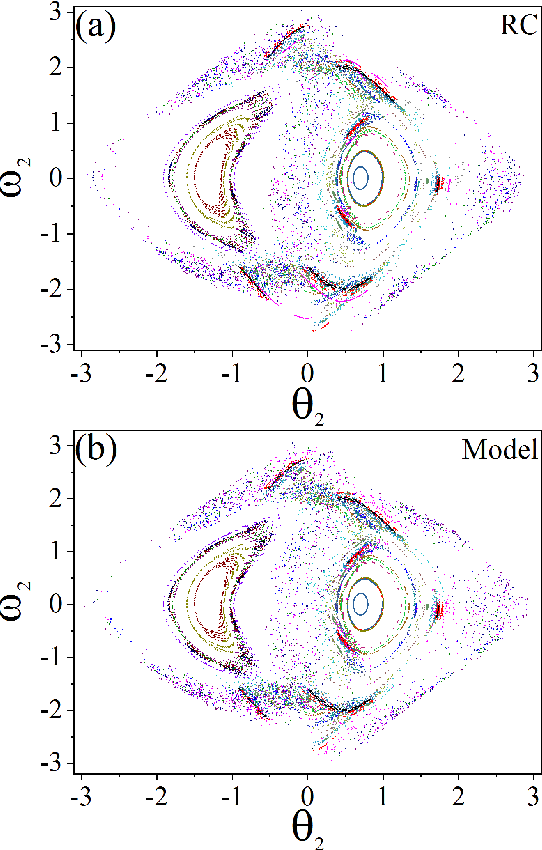

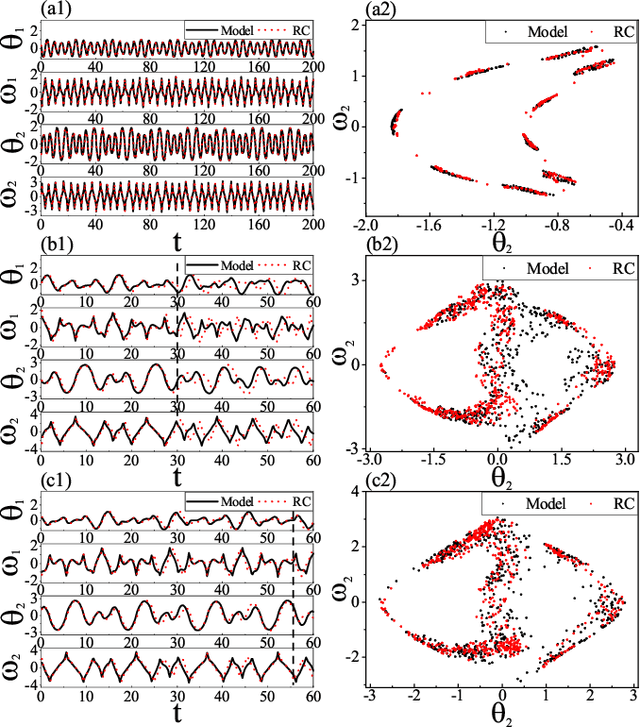
Reconstructing the KAM dynamics diagram of Hamiltonian system from the time series of a limited number of parameters is an outstanding question in nonlinear science, especially when the Hamiltonian governing the system dynamics are unknown. Here, we demonstrate that this question can be addressed by the machine learning approach knowing as reservoir computer (RC). Specifically, we show that without prior knowledge about the Hamilton's equations of motion, the trained RC is able to not only predict the short-term evolution of the system state, but also replicate the long-term ergodic properties of the system dynamics. Furthermore, by the architecture of parameter-aware RC, we also show that the RC trained by the time series acquired at a handful parameters is able to reconstruct the entire KAM dynamics diagram with a high precision by tuning a control parameter externally. The feasibility and efficiency of the learning techniques are demonstrated in two classical nonlinear Hamiltonian systems, namely the double-pendulum oscillator and the standard map. Our study indicates that, as a complex dynamical system, RC is able to learn from data the Hamiltonian.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge