CoNSoLe: Convex Neural Symbolic Learning
Paper and Code
Jun 01, 2022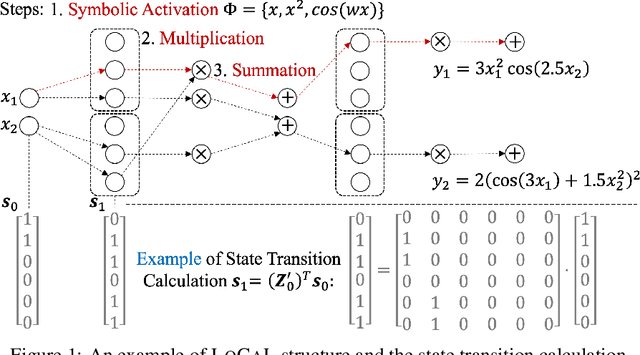

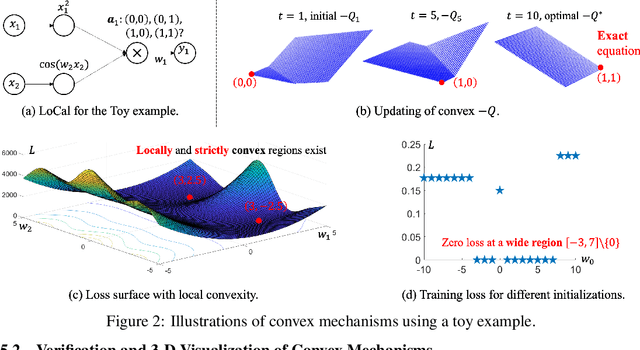
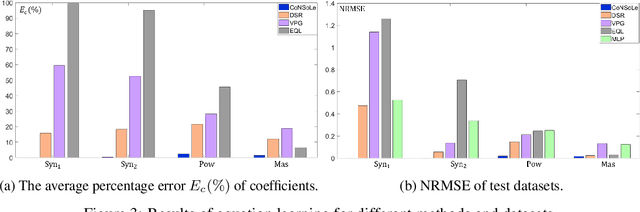
Learning the underlying equation from data is a fundamental problem in many disciplines. Recent advances rely on Neural Networks (NNs) but do not provide theoretical guarantees in obtaining the exact equations owing to the non-convexity of NNs. In this paper, we propose Convex Neural Symbolic Learning (CoNSoLe) to seek convexity under mild conditions. The main idea is to decompose the recovering process into two steps and convexify each step. In the first step of searching for right symbols, we convexify the deep Q-learning. The key is to maintain double convexity for both the negative Q-function and the negative reward function in each iteration, leading to provable convexity of the negative optimal Q function to learn the true symbol connections. Conditioned on the exact searching result, we construct a Locally Convex equation Learner (LoCaL) neural network to convexify the estimation of symbol coefficients. With such a design, we quantify a large region with strict convexity in the loss surface of LoCaL for commonly used physical functions. Finally, we demonstrate the superior performance of the CoNSoLe framework over the state-of-the-art on a diverse set of datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge