Distribution Grid Line Outage Identification with Unknown Pattern and Performance Guarantee

Line outage identification in distribution grids is essential for sustainable grid operation. In this work, we propose a practical yet robust detection approach that utilizes only readily available voltage magnitudes, eliminating the need for costly phase angles or power flow data. Given the sensor data, many existing detection methods based on change-point detection require prior knowledge of outage patterns, which are unknown for real-world outage scenarios. To remove this impractical requirement, we propose a data-driven method to learn the parameters of the post-outage distribution through gradient descent. However, directly using gradient descent presents feasibility issues. To address this, we modify our approach by adding a Bregman divergence constraint to control the trajectory of the parameter updates, which eliminates the feasibility problems. As timely operation is the key nowadays, we prove that the optimal parameters can be learned with convergence guarantees via leveraging the statistical and physical properties of voltage data. We evaluate our approach using many representative distribution grids and real load profiles with 17 outage configurations. The results show that we can detect and localize the outage in a timely manner with only voltage magnitudes and without assuming a prior knowledge of outage patterns.

Quick Line Outage Identification in Urban Distribution Grids via Smart Meters

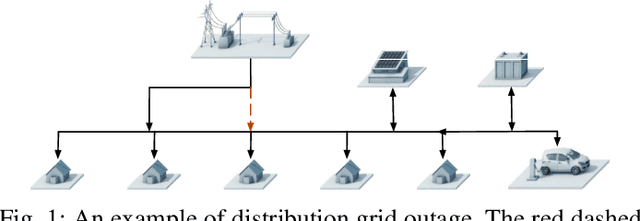
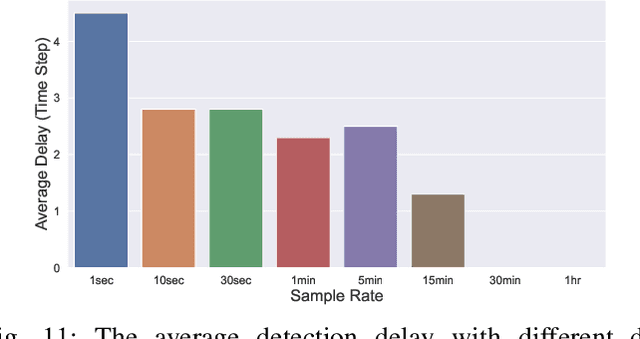
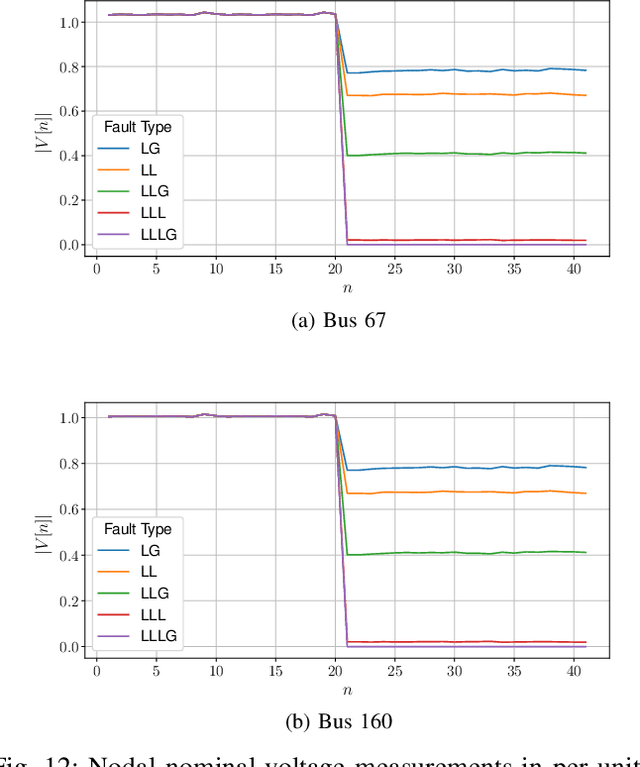
The growing integration of distributed energy resources (DERs) in distribution grids raises various reliability issues due to DER's uncertain and complex behaviors. With a large-scale DER penetration in distribution grids, traditional outage detection methods, which rely on customers report and smart meters' last gasp signals, will have poor performance, because the renewable generators and storages and the mesh structure in urban distribution grids can continue supplying power after line outages. To address these challenges, we propose a data-driven outage monitoring approach based on the stochastic time series analysis with a theoretical guarantee. Specifically, we prove via power flow analysis that the dependency of time-series voltage measurements exhibits significant statistical changes after line outages. This makes the theory on optimal change-point detection suitable to identify line outages. However, existing change point detection methods require post-outage voltage distribution, which is unknown in distribution systems. Therefore, we design a maximum likelihood estimator to directly learn the distribution parameters from voltage data. We prove that the estimated parameters-based detection also achieves the optimal performance, making it extremely useful for fast distribution grid outage identifications. Furthermore, since smart meters have been widely installed in distribution grids and advanced infrastructure (e.g., PMU) has not widely been available, our approach only requires voltage magnitude for quick outage identification. Simulation results show highly accurate outage identification in eight distribution grids with 14 configurations with and without DERs using smart meter data.

Structural Damage Detection and Localization with Unknown Post-Damage Feature Distribution Using Sequential Change-Point Detection Method

The high structural deficient rate poses serious risks to the operation of many bridges and buildings. To prevent critical damage and structural collapse, a quick structural health diagnosis tool is needed during normal operation or immediately after extreme events. In structural health monitoring (SHM), many existing works will have limited performance in the quick damage identification process because 1) the damage event needs to be identified with short delay and 2) the post-damage information is usually unavailable. To address these drawbacks, we propose a new damage detection and localization approach based on stochastic time series analysis. Specifically, the damage sensitive features are extracted from vibration signals and follow different distributions before and after a damage event. Hence, we use the optimal change point detection theory to find damage occurrence time. As the existing change point detectors require the post-damage feature distribution, which is unavailable in SHM, we propose a maximum likelihood method to learn the distribution parameters from the time-series data. The proposed damage detection using estimated parameters also achieves the optimal performance. Also, we utilize the detection results to find damage location without any further computation. Validation results show highly accurate damage identification in American Society of Civil Engineers benchmark structure and two shake table experiments.

Fast Distribution Grid Line Outage Identification with $μ$PMU

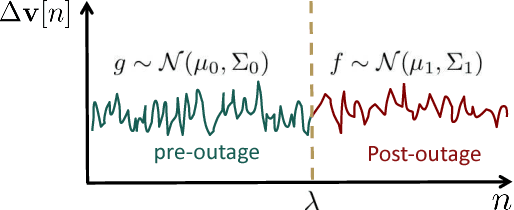
The growing integration of distributed energy resources (DERs) in urban distribution grids raises various reliability issues due to DER's uncertain and complex behaviors. With a large-scale DER penetration, traditional outage detection methods, which rely on customers making phone calls and smart meters' "last gasp" signals, will have limited performance, because the renewable generators can supply powers after line outages and many urban grids are mesh so line outages do not affect power supply. To address these drawbacks, we propose a data-driven outage monitoring approach based on the stochastic time series analysis from micro phasor measurement unit ($\mu$PMU). Specifically, we prove via power flow analysis that the dependency of time-series voltage measurements exhibits significant statistical changes after line outages. This makes the theory on optimal change-point detection suitable to identify line outages via $\mu$PMUs with fast and accurate sampling. However, existing change point detection methods require post-outage voltage distribution unknown in distribution systems. Therefore, we design a maximum likelihood-based method to directly learn the distribution parameters from $\mu$PMU data. We prove that the estimated parameters-based detection still achieves the optimal performance, making it extremely useful for distribution grid outage identifications. Simulation results show highly accurate outage identification in eight distribution grids with 14 configurations with and without DERs using $\mu$PMU data.

Unbalanced Three-Phase Distribution Grid Topology Estimation and Bus Phase Identification

There is an increasing need for monitoring and controlling uncertainties brought by distributed energy resources in distribution grids. For such goal, accurate three-phase topology is the basis for correlating and exterminating measurements in unbalanced distribution networks. Unfortunately, such topology knowledge is often unavailable due to limited investment, especially for secondary distribution grids. Also, the bus phase connectivity information is inaccurate due to human errors or outdated records. For this challenge, we utilize smart meter data at different phases for an information-theoretic approach to learn the structures. Specifically, we convert the system of three unbalanced phasors into symmetrical components, namely the positive, negative, and zero sequences. Then, we prove that Chow-Liu algorithm can find the optimal topology by utilizing power flow equation and the conditional independence relationships implied by the radial three-phase structure of distribution grids with the presence of incorrect bus phase labels. At last, by utilizing Carson's equation, we prove that the bus phase connection can be correctly identified using voltage measurements. For validation, we extensively simulate on IEEE $37$- and $123$-bus systems using real data from PG\&E, ADRES Project, and Pecan Street. We observe that the algorithm is highly accurate for finding three-phase topology in distribution grids even with strong load unbalancing condition and DERs. This ensures close monitoring and controlling DERs in distribution grids.

Urban MV and LV Distribution Grid Topology Estimation via Group Lasso

The increasing penetration of distributed energy resources poses numerous reliability issues to the urban distribution grid. The topology estimation is a critical step to ensure the robustness of distribution grid operation. However, the bus connectivity and grid topology estimation are usually hard in distribution grids. For example, it is technically challenging and costly to monitor the bus connectivity in urban grids, e.g., underground lines. It is also inappropriate to use the radial topology assumption exclusively because the grids of metropolitan cities and regions with dense loads could be with many mesh structures. To resolve these drawbacks, we propose a data-driven topology estimation method for MV and LV distribution grids by only utilizing the historical smart meter measurements. Particularly, a probabilistic graphical model is utilized to capture the statistical dependencies amongst bus voltages. We prove that the bus connectivity and grid topology estimation problems, in radial and mesh structures, can be formulated as a linear regression with a least absolute shrinkage regularization on grouped variables (\textit{group lasso}). Simulations show highly accurate results in eight MV and LV distribution networks at different sizes and 22 topology configurations using PG\&E residential smart meter data.