Kimina-Prover Preview: Towards Large Formal Reasoning Models with Reinforcement Learning

We introduce Kimina-Prover Preview, a large language model that pioneers a novel reasoning-driven exploration paradigm for formal theorem proving, as showcased in this preview release. Trained with a large-scale reinforcement learning pipeline from Qwen2.5-72B, Kimina-Prover demonstrates strong performance in Lean 4 proof generation by employing a structured reasoning pattern we term \textit{formal reasoning pattern}. This approach allows the model to emulate human problem-solving strategies in Lean, iteratively generating and refining proof steps. Kimina-Prover sets a new state-of-the-art on the miniF2F benchmark, reaching 80.7% with pass@8192. Beyond improved benchmark performance, our work yields several key insights: (1) Kimina-Prover exhibits high sample efficiency, delivering strong results even with minimal sampling (pass@1) and scaling effectively with computational budget, stemming from its unique reasoning pattern and RL training; (2) we demonstrate clear performance scaling with model size, a trend previously unobserved for neural theorem provers in formal mathematics; (3) the learned reasoning style, distinct from traditional search algorithms, shows potential to bridge the gap between formal verification and informal mathematical intuition. We open source distilled versions with 1.5B and 7B parameters of Kimina-Prover

Kernel-Based Anomaly Detection Using Generalized Hyperbolic Processes

We present a novel approach to anomaly detection by integrating Generalized Hyperbolic (GH) processes into kernel-based methods. The GH distribution, known for its flexibility in modeling skewness, heavy tails, and kurtosis, helps to capture complex patterns in data that deviate from Gaussian assumptions. We propose a GH-based kernel function and utilize it within Kernel Density Estimation (KDE) and One-Class Support Vector Machines (OCSVM) to develop anomaly detection frameworks. Theoretical results confirmed the positive semi-definiteness and consistency of the GH-based kernel, ensuring its suitability for machine learning applications. Empirical evaluation on synthetic and real-world datasets showed that our method improves detection performance in scenarios involving heavy-tailed and asymmetric or imbalanced distributions. https://github.com/paulinebourigault/GHKernelAnomalyDetect

MVDiff: Scalable and Flexible Multi-View Diffusion for 3D Object Reconstruction from Single-View

Generating consistent multiple views for 3D reconstruction tasks is still a challenge to existing image-to-3D diffusion models. Generally, incorporating 3D representations into diffusion model decrease the model's speed as well as generalizability and quality. This paper proposes a general framework to generate consistent multi-view images from single image or leveraging scene representation transformer and view-conditioned diffusion model. In the model, we introduce epipolar geometry constraints and multi-view attention to enforce 3D consistency. From as few as one image input, our model is able to generate 3D meshes surpassing baselines methods in evaluation metrics, including PSNR, SSIM and LPIPS.

Quaternion recurrent neural network with real-time recurrent learning and maximum correntropy criterion

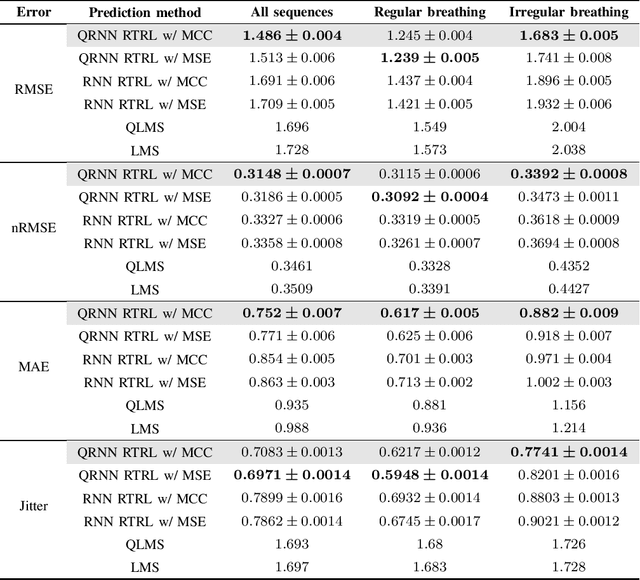
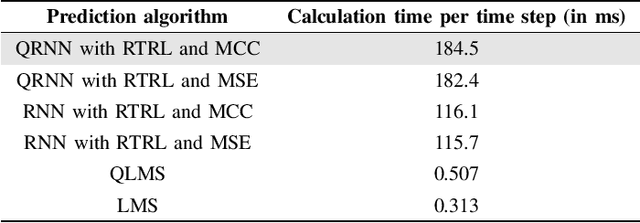
We develop a robust quaternion recurrent neural network (QRNN) for real-time processing of 3D and 4D data with outliers. This is achieved by combining the real-time recurrent learning (RTRL) algorithm and the maximum correntropy criterion (MCC) as a loss function. While both the mean square error and maximum correntropy criterion are viable cost functions, it is shown that the non-quadratic maximum correntropy loss function is less sensitive to outliers, making it suitable for applications with multidimensional noisy or uncertain data. Both algorithms are derived based on the novel generalised HR (GHR) calculus, which allows for the differentiation of real functions of quaternion variables and offers the product and chain rules, thus enabling elegant and compact derivations. Simulation results in the context of motion prediction of chest internal markers for lung cancer radiotherapy, which includes regular and irregular breathing sequences, support the analysis.

The HR-Calculus: Enabling Information Processing with Quaternion Algebra

From their inception, quaternions and their division algebra have proven to be advantageous in modelling rotation/orientation in three-dimensional spaces and have seen use from the initial formulation of electromagnetic filed theory through to forming the basis of quantum filed theory. Despite their impressive versatility in modelling real-world phenomena, adaptive information processing techniques specifically designed for quaternion-valued signals have only recently come to the attention of the machine learning, signal processing, and control communities. The most important development in this direction is introduction of the HR-calculus, which provides the required mathematical foundation for deriving adaptive information processing techniques directly in the quaternion domain. In this article, the foundations of the HR-calculus are revised and the required tools for deriving adaptive learning techniques suitable for dealing with quaternion-valued signals, such as the gradient operator, chain and product derivative rules, and Taylor series expansion are presented. This serves to establish the most important applications of adaptive information processing in the quaternion domain for both single-node and multi-node formulations. The article is supported by Supplementary Material, which will be referred to as SM.

Convex Quaternion Optimization for Signal Processing: Theory and Applications

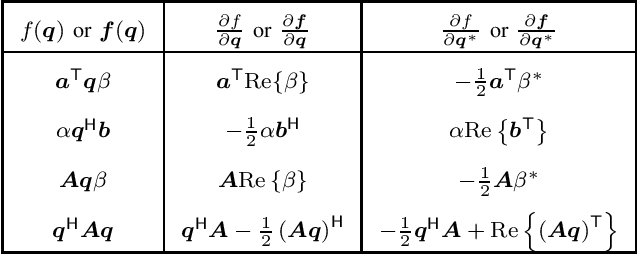
Convex optimization methods have been extensively used in the fields of communications and signal processing. However, the theory of quaternion optimization is currently not as fully developed and systematic as that of complex and real optimization. To this end, we establish an essential theory of convex quaternion optimization for signal processing based on the generalized Hamilton-real (GHR) calculus. This is achieved in a way which conforms with traditional complex and real optimization theory. For rigorous, We present five discriminant theorems for convex quaternion functions, and four discriminant criteria for strongly convex quaternion functions. Furthermore, we provide a fundamental theorem for the optimality of convex quaternion optimization problems, and demonstrate its utility through three applications in quaternion signal processing. These results provide a solid theoretical foundation for convex quaternion optimization and open avenues for further developments in signal processing applications.