The HR-Calculus: Enabling Information Processing with Quaternion Algebra

From their inception, quaternions and their division algebra have proven to be advantageous in modelling rotation/orientation in three-dimensional spaces and have seen use from the initial formulation of electromagnetic filed theory through to forming the basis of quantum filed theory. Despite their impressive versatility in modelling real-world phenomena, adaptive information processing techniques specifically designed for quaternion-valued signals have only recently come to the attention of the machine learning, signal processing, and control communities. The most important development in this direction is introduction of the HR-calculus, which provides the required mathematical foundation for deriving adaptive information processing techniques directly in the quaternion domain. In this article, the foundations of the HR-calculus are revised and the required tools for deriving adaptive learning techniques suitable for dealing with quaternion-valued signals, such as the gradient operator, chain and product derivative rules, and Taylor series expansion are presented. This serves to establish the most important applications of adaptive information processing in the quaternion domain for both single-node and multi-node formulations. The article is supported by Supplementary Material, which will be referred to as SM.

Reciprocal Adversarial Learning via Characteristic Functions

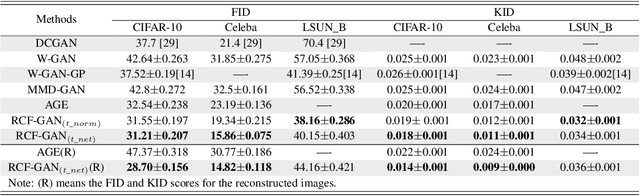
Generative adversarial nets (GANs) have become a preferred tool for accommodating complicated distributions, and to stabilise the training and reduce the mode collapse of GANs, one of their main variants employs the integral probability metric (IPM) as the loss function. Although theoretically supported, extensive IPM-GANs are basically comparing moments in an embedded domain of the \textit{critic}. We generalise this by comparing the distributions rather than the moments via a powerful tool, i.e., the characteristic function (CF), which uniquely and universally contains all the information about a distribution. For rigour, we first establish the physical meaning of the phase and amplitude in CFs. This provides a feasible way of manipulating the generation. We then develop an efficient sampling way to calculate the CFs. Within this framework, we further prove an equivalence between the embedded and data domains when a reciprocal exists, which allows us to develop the GAN in an auto-encoder way, by using only two modules to achieve bi-directionally generating clear images. We refer to this efficient structure as the reciprocal CF GAN (RCF-GAN). Experimental results show the superior performances of the proposed RCF-GAN in terms of both generation and reconstruction.

A general solver to the elliptical mixture model through an approximate Wasserstein manifold

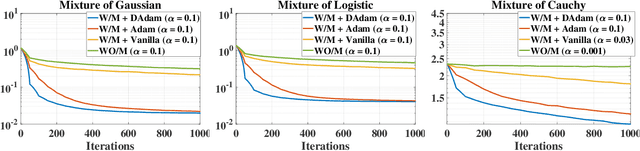
This paper studies the problem of estimation for general finite mixture models, with a particular focus on the elliptical mixture models (EMMs). Instead of using the widely adopted Kullback-Leibler divergence, we provide a stable solution to the EMMs that is robust to initialisations and attains superior local optimum by adaptively optimising along a manifold of an approximate Wasserstein distance. More specifically, we first summarise computable and identifiable EMMs, in order to identify the optimisation problem. Due to a probability constraint, solving this problem is cumbersome and unstable, especially under the Wasserstein distance. We thus resort to an efficient optimisation on a statistical manifold defined under an approximate Wasserstein distance, which allows for explicit metrics and operations. This is shown to significantly stabilise and improve the EMM estimations. We also propose an adaptive method to further accelerate the convergence. Experimental results demonstrate excellent performances of the proposed solver.