Danilo P. Mandic
TensorSLM: Energy-efficient Embedding Compression of Sub-billion Parameter Language Models on Low-end Devices
Jun 16, 2025Abstract:Small Language Models (SLMs, or on-device LMs) have significantly fewer parameters than Large Language Models (LLMs). They are typically deployed on low-end devices, like mobile phones and single-board computers. Unlike LLMs, which rely on increasing model size for better generalisation, SLMs designed for edge applications are expected to have adaptivity to the deployment environments and energy efficiency given the device battery life constraints, which are not addressed in datacenter-deployed LLMs. This paper addresses these two requirements by proposing a training-free token embedding compression approach using Tensor-Train Decomposition (TTD). Each pre-trained token embedding vector is converted into a lower-dimensional Matrix Product State (MPS). We comprehensively evaluate the extracted low-rank structures across compression ratio, language task performance, latency, and energy consumption on a typical low-end device, i.e. Raspberry Pi. Taking the sub-billion parameter versions of GPT-2/Cerebres-GPT and OPT models as examples, our approach achieves a comparable language task performance to the original model with around $2.0\times$ embedding layer compression, while the energy consumption of a single query drops by half.
Versatile Cardiovascular Signal Generation with a Unified Diffusion Transformer
May 28, 2025Abstract:Cardiovascular signals such as photoplethysmography (PPG), electrocardiography (ECG), and blood pressure (BP) are inherently correlated and complementary, together reflecting the health of cardiovascular system. However, their joint utilization in real-time monitoring is severely limited by diverse acquisition challenges from noisy wearable recordings to burdened invasive procedures. Here we propose UniCardio, a multi-modal diffusion transformer that reconstructs low-quality signals and synthesizes unrecorded signals in a unified generative framework. Its key innovations include a specialized model architecture to manage the signal modalities involved in generation tasks and a continual learning paradigm to incorporate varying modality combinations. By exploiting the complementary nature of cardiovascular signals, UniCardio clearly outperforms recent task-specific baselines in signal denoising, imputation, and translation. The generated signals match the performance of ground-truth signals in detecting abnormal health conditions and estimating vital signs, even in unseen domains, while ensuring interpretability for human experts. These advantages position UniCardio as a promising avenue for advancing AI-assisted healthcare.
A Quantum of Learning: Using Quaternion Algebra to Model Learning on Quantum Devices
Apr 17, 2025Abstract:This article considers the problem of designing adaption and optimisation techniques for training quantum learning machines. To this end, the division algebra of quaternions is used to derive an effective model for representing computation and measurement operations on qubits. In turn, the derived model, serves as the foundation for formulating an adaptive learning problem on principal quantum learning units, thereby establishing quantum information processing units akin to that of neurons in classical approaches. Then, leveraging the modern HR-calculus, a comprehensive training framework for learning on quantum machines is developed. The quaternion-valued model accommodates mathematical tractability and establishment of performance criteria, such as convergence conditions.
How can representation dimension dominate structurally pruned LLMs?
Mar 06, 2025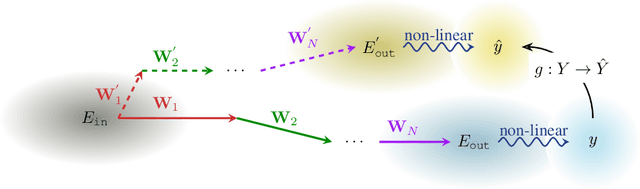



Abstract:Pruning assumes a subnetwork exists in the original deep neural network, which can achieve comparative model performance with less computation than the original. However, it is unclear how the model performance varies with the different subnetwork extractions. In this paper, we choose the representation dimension (or embedding dimension, model dimension, the dimension of the residual stream in the relevant literature) as the entry point to this issue. We investigate the linear transformations in the LLM transformer blocks and consider a specific structured pruning approach, SliceGPT, to extract the subnetworks of different representation dimensions. We mechanistically analyse the activation flow during the model forward passes, and find the representation dimension dominates the linear transformations, model predictions, and, finally, the model performance. Explicit analytical relations are given to calculate the pruned model performance (perplexity and accuracy) without actual evaluation, and are empirically validated with Llama-3-8B-Instruct and Phi-3-mini-4k-Instruct.
Kernel-Based Anomaly Detection Using Generalized Hyperbolic Processes
Jan 25, 2025



Abstract:We present a novel approach to anomaly detection by integrating Generalized Hyperbolic (GH) processes into kernel-based methods. The GH distribution, known for its flexibility in modeling skewness, heavy tails, and kurtosis, helps to capture complex patterns in data that deviate from Gaussian assumptions. We propose a GH-based kernel function and utilize it within Kernel Density Estimation (KDE) and One-Class Support Vector Machines (OCSVM) to develop anomaly detection frameworks. Theoretical results confirmed the positive semi-definiteness and consistency of the GH-based kernel, ensuring its suitability for machine learning applications. Empirical evaluation on synthetic and real-world datasets showed that our method improves detection performance in scenarios involving heavy-tailed and asymmetric or imbalanced distributions. https://github.com/paulinebourigault/GHKernelAnomalyDetect
Targeted Angular Reversal of Weights (TARS) for Knowledge Removal in Large Language Models
Dec 13, 2024Abstract:The sheer scale of data required to train modern large language models (LLMs) poses significant risks, as models are likely to gain knowledge of sensitive topics such as bio-security, as well the ability to replicate copyrighted works. Methods designed to remove such knowledge must do so from all prompt directions, in a multi-lingual capacity and without degrading general model performance. To this end, we introduce the targeted angular reversal (TARS) method of knowledge removal from LLMs. The TARS method firstly leverages the LLM in combination with a detailed prompt to aggregate information about a selected concept in the internal representation space of the LLM. It then refines this approximate concept vector to trigger the concept token with high probability, by perturbing the approximate concept vector with noise and transforming it into token scores with the language model head. The feedforward weight vectors in the LLM which operate directly on the internal representation space, and have the highest cosine similarity with this targeting vector, are then replaced by a reversed targeting vector, thus limiting the ability of the concept to propagate through the model. The modularity of the TARS method allows for a sequential removal of concepts from Llama 3.1 8B, such as the famous literary detective Sherlock Holmes, and the planet Saturn. It is demonstrated that the probability of triggering target concepts can be reduced to 0.00 with as few as 1 TARS edit, whilst simultaneously removing the knowledge bi-directionally. Moreover, knowledge is shown to be removed across all languages despite only being targeted in English. Importantly, TARS has minimal impact on the general model capabilities, as after removing 5 diverse concepts in a modular fashion, there is minimal KL divergence in the next token probabilities of the LLM on large corpora of Wikipedia text (median of 0.002).
Geometry is All You Need: A Unified Taxonomy of Matrix and Tensor Factorization for Compression of Generative Language Models
Oct 03, 2024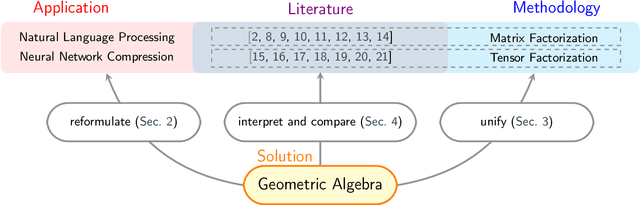

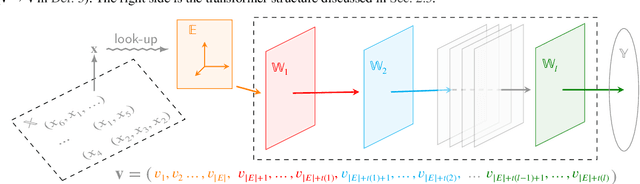
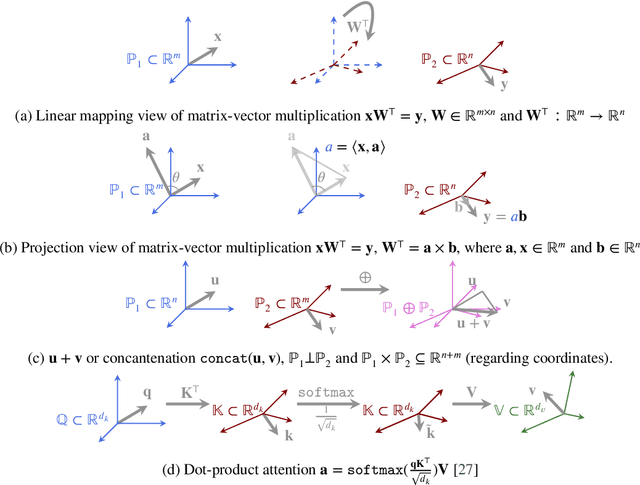
Abstract:Matrix and tensor-guided parametrization for Natural Language Processing (NLP) models is fundamentally useful for the improvement of the model's systematic efficiency. However, the internal links between these two algebra structures and language model parametrization are poorly understood. Also, the existing matrix and tensor research is math-heavy and far away from machine learning (ML) and NLP research concepts. These two issues result in the recent progress on matrices and tensors for model parametrization being more like a loose collection of separate components from matrix/tensor and NLP studies, rather than a well-structured unified approach, further hindering algorithm design. To this end, we propose a unified taxonomy, which bridges the matrix/tensor compression approaches and model compression concepts in ML and NLP research. Namely, we adopt an elementary concept in linear algebra, that of a subspace, which is also the core concept in geometric algebra, to reformulate the matrix/tensor and ML/NLP concepts (e.g. attention mechanism) under one umbrella. In this way, based on our subspace formalization, typical matrix and tensor decomposition algorithms can be interpreted as geometric transformations. Finally, we revisit recent literature on matrix- or tensor-guided language model compression, rephrase and compare their core ideas, and then point out the current research gap and potential solutions.
In-ear ECG Signal Enhancement with Denoising Convolutional Autoencoders
Aug 27, 2024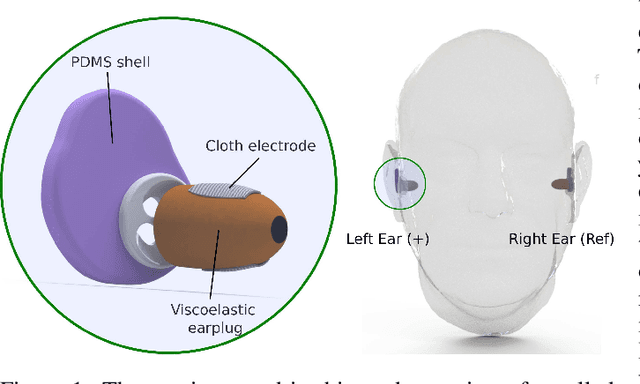
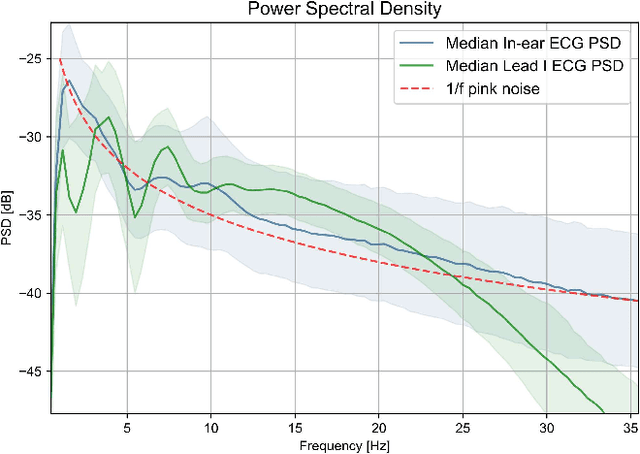
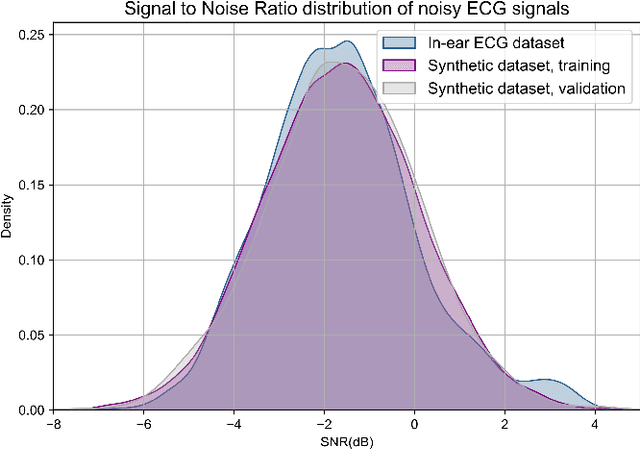
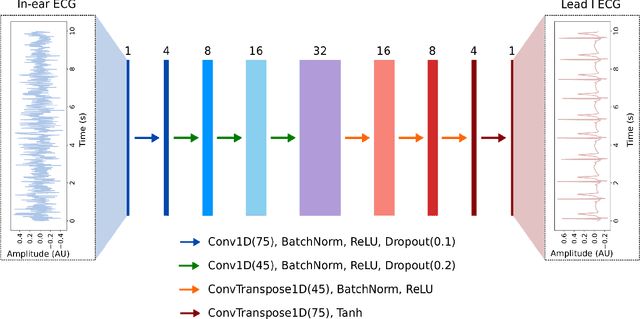
Abstract:The cardiac dipole has been shown to propagate to the ears, now a common site for consumer wearable electronics, enabling the recording of electrocardiogram (ECG) signals. However, in-ear ECG recordings often suffer from significant noise due to their small amplitude and the presence of other physiological signals, such as electroencephalogram (EEG), which complicates the extraction of cardiovascular features. This study addresses this issue by developing a denoising convolutional autoencoder (DCAE) to enhance ECG information from in-ear recordings, producing cleaner ECG outputs. The model is evaluated using a dataset of in-ear ECGs and corresponding clean Lead I ECGs from 45 healthy participants. The results demonstrate a substantial improvement in signal-to-noise ratio (SNR), with a median increase of 5.9 dB. Additionally, the model significantly improved heart rate estimation accuracy, reducing the mean absolute error by almost 70% and increasing R-peak detection precision to a median value of 90%. We also trained and validated the model using a synthetic dataset, generated from real ECG signals, including abnormal cardiac morphologies, corrupted by pink noise. The results obtained show effective removal of noise sources with clinically plausible waveform reconstruction ability.
Interpretable Pre-Trained Transformers for Heart Time-Series Data
Jul 30, 2024Abstract:Decoder-only transformers are the backbone of the popular generative pre-trained transformer (GPT) series of large language models. In this work, we apply the same framework to periodic heart time-series data to create two pre-trained general purpose cardiac models, namely PPG-PT and ECG-PT. We demonstrate that both such pre-trained models are fully interpretable. This is achieved firstly through aggregate attention maps which show that the model focuses on similar points in previous cardiac cycles in order to make predictions and gradually broadens its attention in deeper layers. Next, tokens with the same value, that occur at different distinct points in the ECG and PPG cycle, form separate clusters in high dimensional space based on their phase as they propagate through the transformer blocks. Finally, we highlight that individual attention heads respond to specific physiologically relevent features, such as the dicrotic notch in PPG and the P-wave in ECG. It is also demonstrated that these pre-trained models can be easily fine-tuned for tasks such as classification of atrial fibrillation. In this specific example, the fine-tuning took 11 minutes of computer time, and achieved a leave-one-subject-out AUCs of 0.99 and 0.93 for ECG and PPG respectively. Importantly, these fine-tuned models are also fully explainable, with attention shifting to regions in the context that are strongly indicative of atrial fibrillation.
Demystifying the Hypercomplex: Inductive Biases in Hypercomplex Deep Learning
May 11, 2024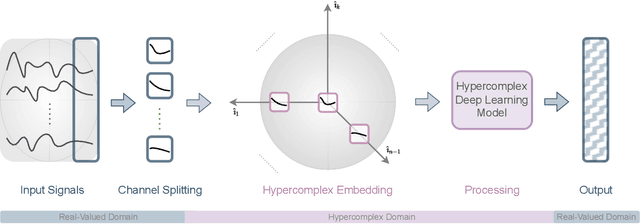
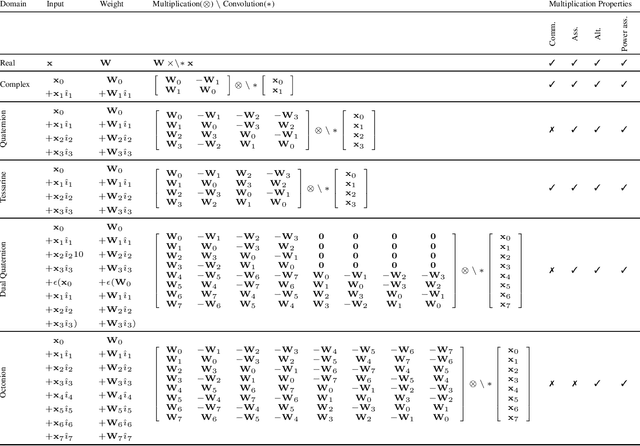
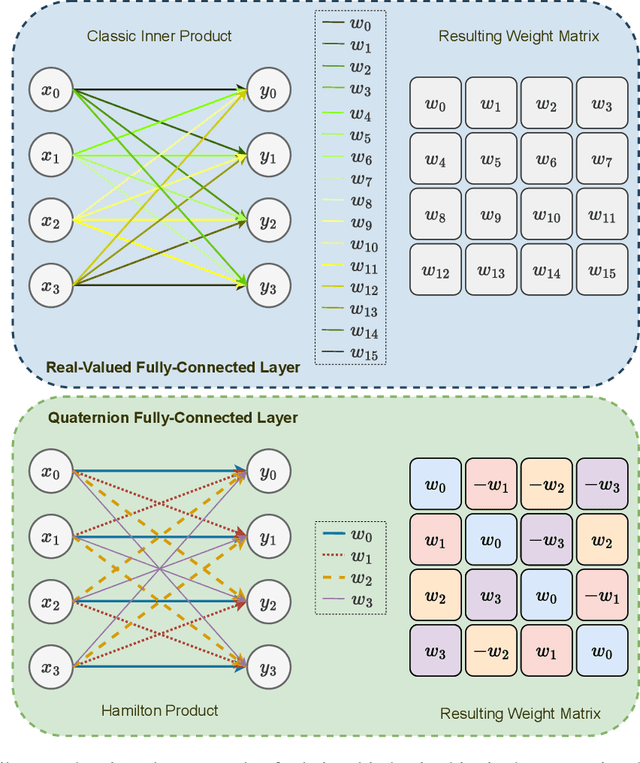
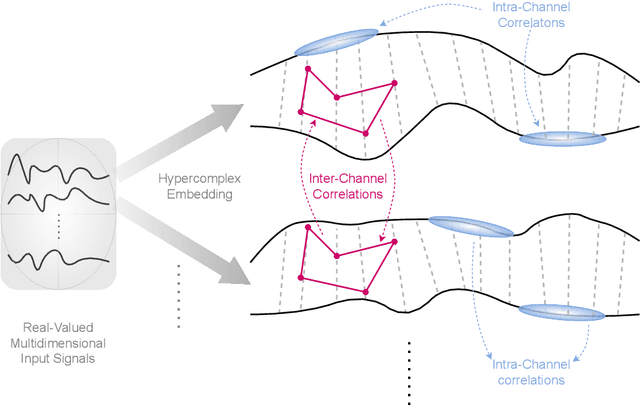
Abstract:Hypercomplex algebras have recently been gaining prominence in the field of deep learning owing to the advantages of their division algebras over real vector spaces and their superior results when dealing with multidimensional signals in real-world 3D and 4D paradigms. This paper provides a foundational framework that serves as a roadmap for understanding why hypercomplex deep learning methods are so successful and how their potential can be exploited. Such a theoretical framework is described in terms of inductive bias, i.e., a collection of assumptions, properties, and constraints that are built into training algorithms to guide their learning process toward more efficient and accurate solutions. We show that it is possible to derive specific inductive biases in the hypercomplex domains, which extend complex numbers to encompass diverse numbers and data structures. These biases prove effective in managing the distinctive properties of these domains, as well as the complex structures of multidimensional and multimodal signals. This novel perspective for hypercomplex deep learning promises to both demystify this class of methods and clarify their potential, under a unifying framework, and in this way promotes hypercomplex models as viable alternatives to traditional real-valued deep learning for multidimensional signal processing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge