Demystifying the Hypercomplex: Inductive Biases in Hypercomplex Deep Learning

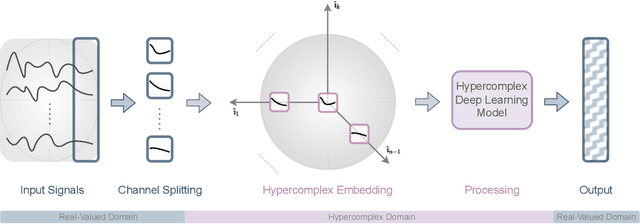
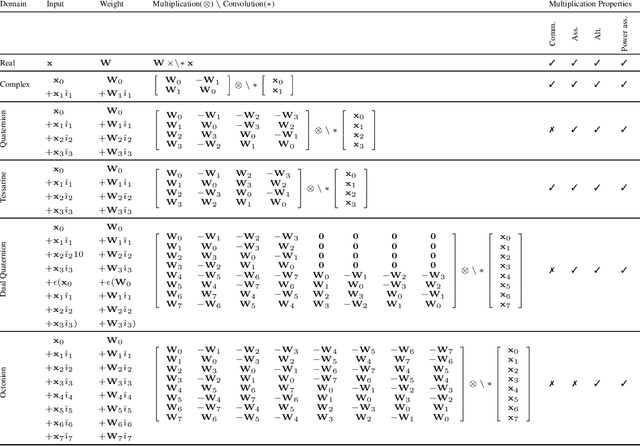
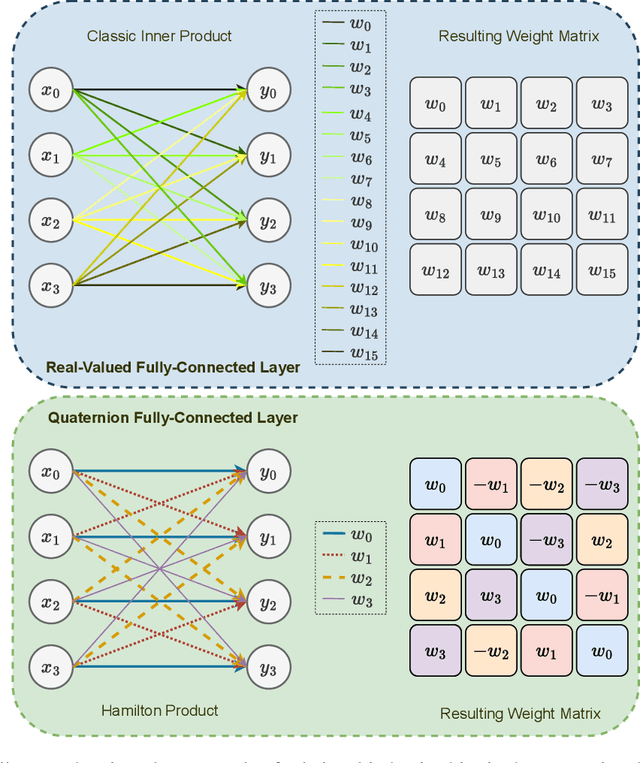
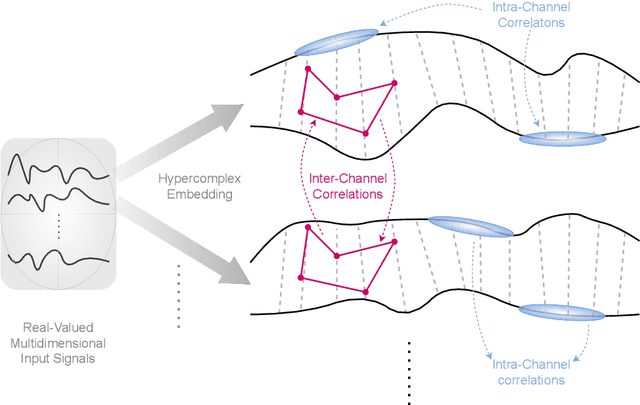
Hypercomplex algebras have recently been gaining prominence in the field of deep learning owing to the advantages of their division algebras over real vector spaces and their superior results when dealing with multidimensional signals in real-world 3D and 4D paradigms. This paper provides a foundational framework that serves as a roadmap for understanding why hypercomplex deep learning methods are so successful and how their potential can be exploited. Such a theoretical framework is described in terms of inductive bias, i.e., a collection of assumptions, properties, and constraints that are built into training algorithms to guide their learning process toward more efficient and accurate solutions. We show that it is possible to derive specific inductive biases in the hypercomplex domains, which extend complex numbers to encompass diverse numbers and data structures. These biases prove effective in managing the distinctive properties of these domains, as well as the complex structures of multidimensional and multimodal signals. This novel perspective for hypercomplex deep learning promises to both demystify this class of methods and clarify their potential, under a unifying framework, and in this way promotes hypercomplex models as viable alternatives to traditional real-valued deep learning for multidimensional signal processing.