Yao Lei Xu
TensorSLM: Energy-efficient Embedding Compression of Sub-billion Parameter Language Models on Low-end Devices
Jun 16, 2025Abstract:Small Language Models (SLMs, or on-device LMs) have significantly fewer parameters than Large Language Models (LLMs). They are typically deployed on low-end devices, like mobile phones and single-board computers. Unlike LLMs, which rely on increasing model size for better generalisation, SLMs designed for edge applications are expected to have adaptivity to the deployment environments and energy efficiency given the device battery life constraints, which are not addressed in datacenter-deployed LLMs. This paper addresses these two requirements by proposing a training-free token embedding compression approach using Tensor-Train Decomposition (TTD). Each pre-trained token embedding vector is converted into a lower-dimensional Matrix Product State (MPS). We comprehensively evaluate the extracted low-rank structures across compression ratio, language task performance, latency, and energy consumption on a typical low-end device, i.e. Raspberry Pi. Taking the sub-billion parameter versions of GPT-2/Cerebres-GPT and OPT models as examples, our approach achieves a comparable language task performance to the original model with around $2.0\times$ embedding layer compression, while the energy consumption of a single query drops by half.
TensorGPT: Efficient Compression of the Embedding Layer in LLMs based on the Tensor-Train Decomposition
Jul 02, 2023



Abstract:High-dimensional token embeddings underpin Large Language Models (LLMs), as they can capture subtle semantic information and significantly enhance the modelling of complex language patterns. However, the associated high dimensionality also introduces considerable model parameters, and a prohibitively high model storage. To address this issue, this work proposes an approach based on the Tensor-Train Decomposition (TTD), where each token embedding is treated as a Matrix Product State (MPS) that can be efficiently computed in a distributed manner. The experimental results on GPT-2 demonstrate that, through our approach, the embedding layer can be compressed by a factor of up to 38.40 times, and when the compression factor is 3.31 times, even produced a better performance than the original GPT-2 model.
Graph Tensor Networks: An Intuitive Framework for Designing Large-Scale Neural Learning Systems on Multiple Domains
Mar 23, 2023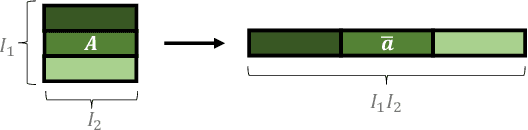
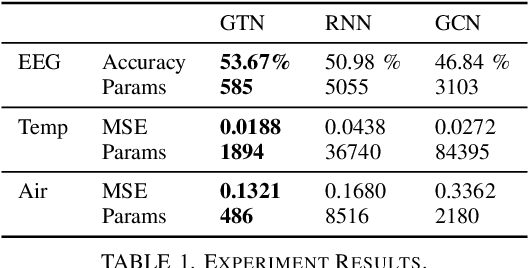
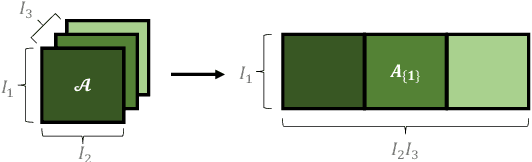
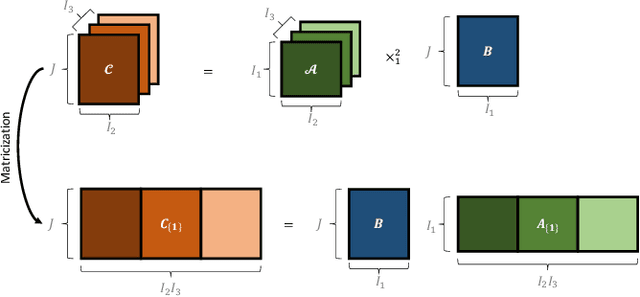
Abstract:Despite the omnipresence of tensors and tensor operations in modern deep learning, the use of tensor mathematics to formally design and describe neural networks is still under-explored within the deep learning community. To this end, we introduce the Graph Tensor Network (GTN) framework, an intuitive yet rigorous graphical framework for systematically designing and implementing large-scale neural learning systems on both regular and irregular domains. The proposed framework is shown to be general enough to include many popular architectures as special cases, and flexible enough to handle data on any and many data domains. The power and flexibility of the proposed framework is demonstrated through real-data experiments, resulting in improved performance at a drastically lower complexity costs, by virtue of tensor algebra.
Complexity-based Financial Stress Evaluation
Dec 05, 2022Abstract:Financial markets typically exhibit dynamically complex properties as they undergo continuous interactions with economic and environmental factors. The Efficient Market Hypothesis indicates a rich difference in the structural complexity of security prices between normal (stable markets) and abnormal (financial crises) situations. Considering the analogy between market undulation of price time series and physical stress of bio-signals, we investigate whether stress indices in bio-systems can be adopted and modified so as to measure 'standard stress' in financial markets. This is achieved by employing structural complexity analysis, based on variants of univariate and multivariate sample entropy, to estimate the stress level of both financial markets on the whole and the performance of the individual financial indices. Further, we propose a novel graphical framework to establish the sensitivity of individual assets and stock markets to financial crises. This is achieved through Catastrophe Theory and entropy-based stress evaluations indicating the unique performance of each index/individual stock in response to different crises. Four major indices and four individual equities with gold prices are considered over the past 32 years from 1991-2021. Our findings based on nonlinear analyses and the proposed framework support the Efficient Market Hypothesis and reveal the relations among economic indices and within each price time series.
Graph-Regularized Tensor Regression: A Domain-Aware Framework for Interpretable Multi-Way Financial Modelling
Oct 26, 2022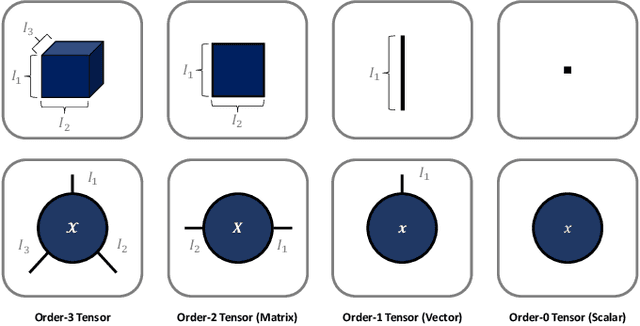
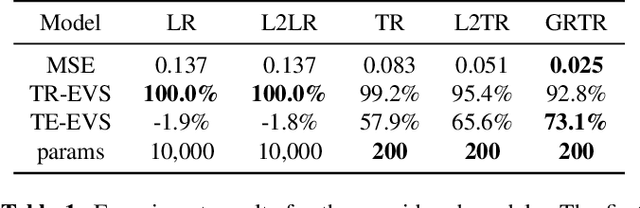
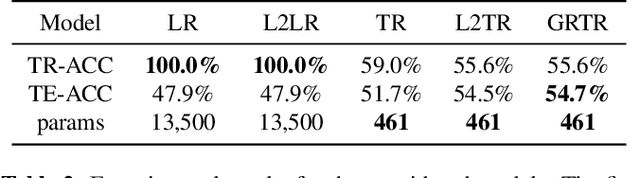
Abstract:Analytics of financial data is inherently a Big Data paradigm, as such data are collected over many assets, asset classes, countries, and time periods. This represents a challenge for modern machine learning models, as the number of model parameters needed to process such data grows exponentially with the data dimensions; an effect known as the Curse-of-Dimensionality. Recently, Tensor Decomposition (TD) techniques have shown promising results in reducing the computational costs associated with large-dimensional financial models while achieving comparable performance. However, tensor models are often unable to incorporate the underlying economic domain knowledge. To this end, we develop a novel Graph-Regularized Tensor Regression (GRTR) framework, whereby knowledge about cross-asset relations is incorporated into the model in the form of a graph Laplacian matrix. This is then used as a regularization tool to promote an economically meaningful structure within the model parameters. By virtue of tensor algebra, the proposed framework is shown to be fully interpretable, both coefficient-wise and dimension-wise. The GRTR model is validated in a multi-way financial forecasting setting and compared against competing models, and is shown to achieve improved performance at reduced computational costs. Detailed visualizations are provided to help the reader gain an intuitive understanding of the employed tensor operations.
Graph Theory for Metro Traffic Modelling
May 11, 2021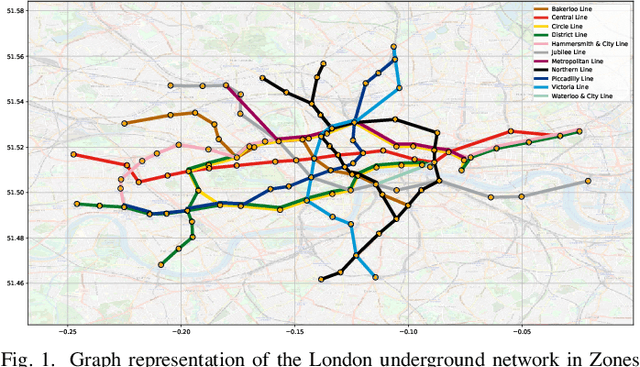
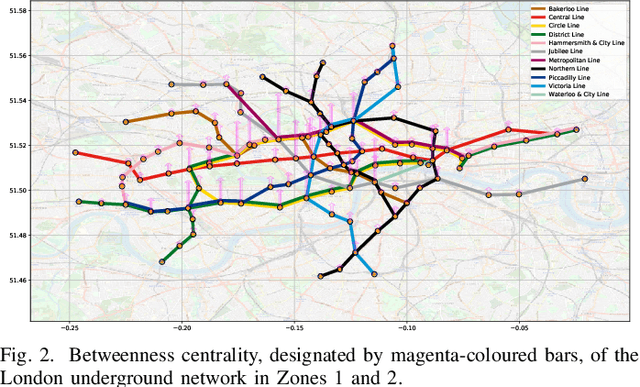
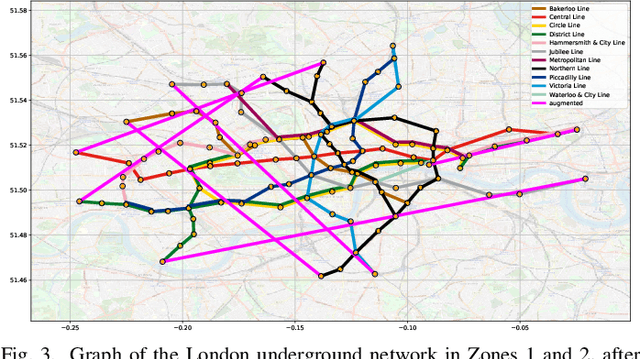
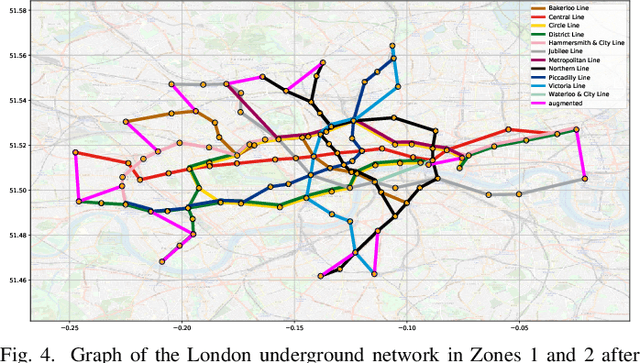
Abstract:A unifying graph theoretic framework for the modelling of metro transportation networks is proposed. This is achieved by first introducing a basic graph framework for the modelling of the London underground system from a diffusion law point of view. This forms a basis for the analysis of both station importance and their vulnerability, whereby the concept of graph vertex centrality plays a key role. We next explore k-edge augmentation of a graph topology, and illustrate its usefulness both for improving the network robustness and as a planning tool. Upon establishing the graph theoretic attributes of the underlying graph topology, we proceed to introduce models for processing data on such a metro graph. Commuter movement is shown to obey the Fick's law of diffusion, where the graph Laplacian provides an analytical model for the diffusion process of commuter population dynamics. Finally, we also explore the application of modern deep learning models, such as graph neural networks and hyper-graph neural networks, as general purpose models for the modelling and forecasting of underground data, especially in the context of the morning and evening rush hours. Comprehensive simulations including the passenger in- and out-flows during the morning rush hour in London demonstrates the advantages of the graph models in metro planning and traffic management, a formal mathematical approach with wide economic implications.
Tensor-Train Recurrent Neural Networks for Interpretable Multi-Way Financial Forecasting
May 11, 2021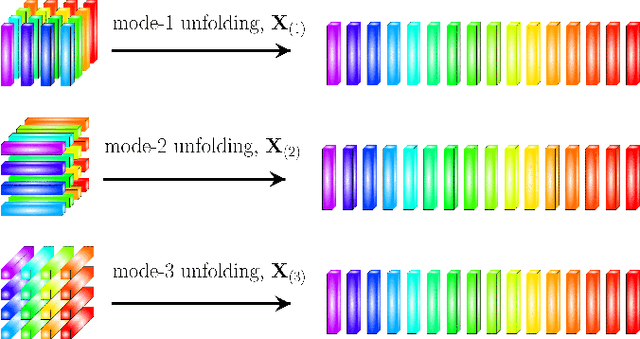
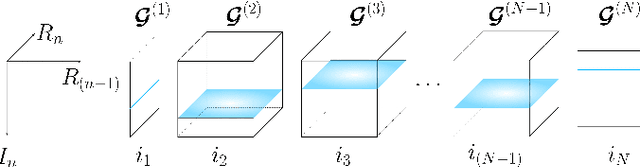

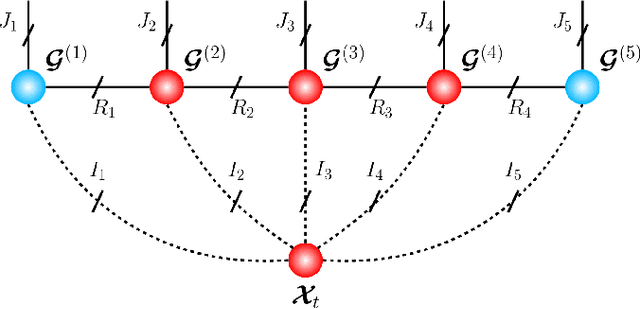
Abstract:Recurrent Neural Networks (RNNs) represent the de facto standard machine learning tool for sequence modelling, owing to their expressive power and memory. However, when dealing with large dimensional data, the corresponding exponential increase in the number of parameters imposes a computational bottleneck. The necessity to equip RNNs with the ability to deal with the curse of dimensionality, such as through the parameter compression ability inherent to tensors, has led to the development of the Tensor-Train RNN (TT-RNN). Despite achieving promising results in many applications, the full potential of the TT-RNN is yet to be explored in the context of interpretable financial modelling, a notoriously challenging task characterized by multi-modal data with low signal-to-noise ratio. To address this issue, we investigate the potential of TT-RNN in the task of financial forecasting of currencies. We show, through the analysis of TT-factors, that the physical meaning underlying tensor decomposition, enables the TT-RNN model to aid the interpretability of results, thus mitigating the notorious "black-box" issue associated with neural networks. Furthermore, simulation results highlight the regularization power of TT decomposition, demonstrating the superior performance of TT-RNN over its uncompressed RNN counterpart and other tensor forecasting methods.
Tensor Networks for Multi-Modal Non-Euclidean Data
Mar 27, 2021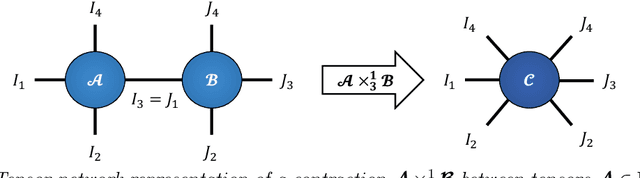
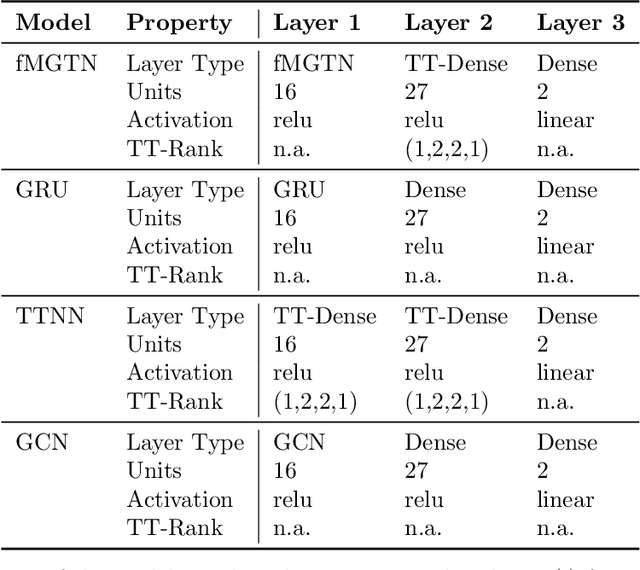
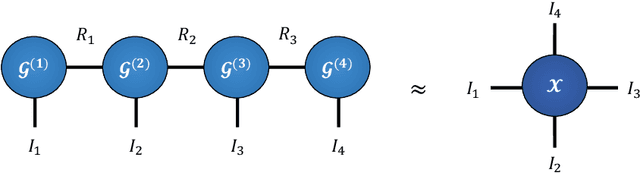
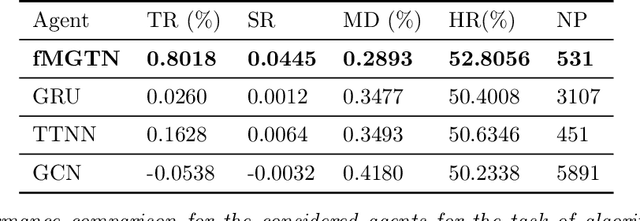
Abstract:Modern data sources are typically of large scale and multi-modal natures, and acquired on irregular domains, which poses serious challenges to traditional deep learning models. These issues are partially mitigated by either extending existing deep learning algorithms to irregular domains through graphs, or by employing tensor methods to alleviate the computational bottlenecks imposed by the Curse of Dimensionality. To simultaneously resolve both these issues, we introduce a novel Multi-Graph Tensor Network (MGTN) framework, which leverages on the desirable properties of graphs, tensors and neural networks in a physically meaningful and compact manner. This equips MGTNs with the ability to exploit local information in irregular data sources at a drastically reduced parameter complexity, and over a range of learning paradigms such as regression, classification and reinforcement learning. The benefits of the MGTN framework, especially its ability to avoid overfitting through the inherent low-rank regularization properties of tensor networks, are demonstrated through its superior performance against competing models in the individual tensor, graph, and neural network domains.
Multi-Graph Tensor Networks
Nov 11, 2020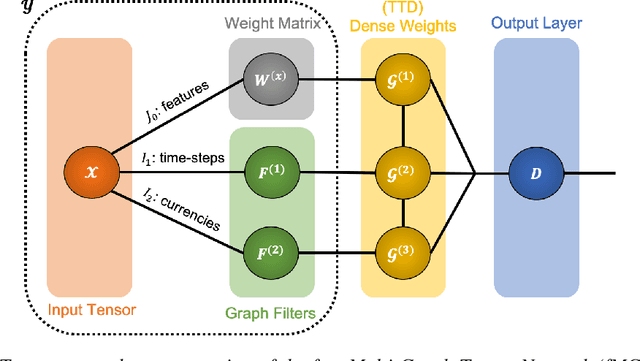
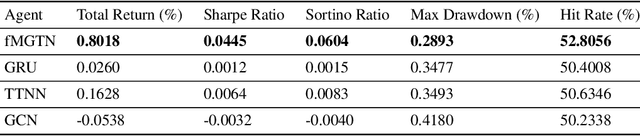
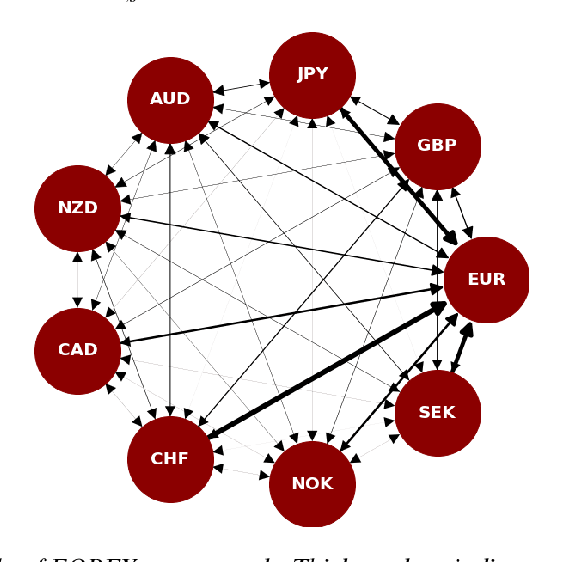
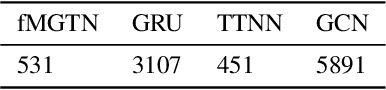
Abstract:The irregular and multi-modal nature of numerous modern data sources poses serious challenges for traditional deep learning algorithms. To this end, recent efforts have generalized existing algorithms to irregular domains through graphs, with the aim to gain additional insights from data through the underlying graph topology. At the same time, tensor-based methods have demonstrated promising results in bypassing the bottlenecks imposed by the Curse of Dimensionality. In this paper, we introduce a novel Multi-Graph Tensor Network (MGTN) framework, which exploits both the ability of graphs to handle irregular data sources and the compression properties of tensor networks in a deep learning setting. The potential of the proposed framework is demonstrated through an MGTN based deep Q agent for Foreign Exchange (FOREX) algorithmic trading. By virtue of the MGTN, a FOREX currency graph is leveraged to impose an economically meaningful structure on this demanding task, resulting in a highly superior performance against three competing models and at a drastically lower complexity.
Recurrent Graph Tensor Networks
Oct 17, 2020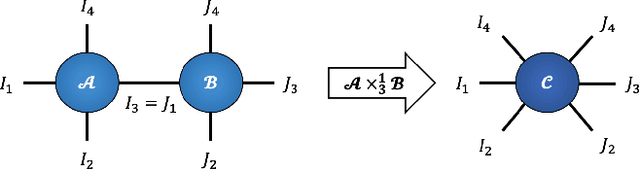

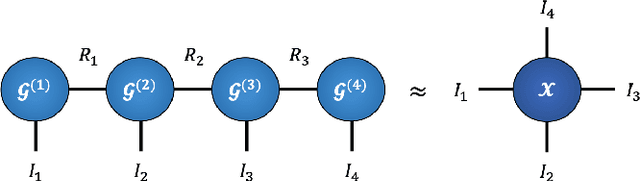
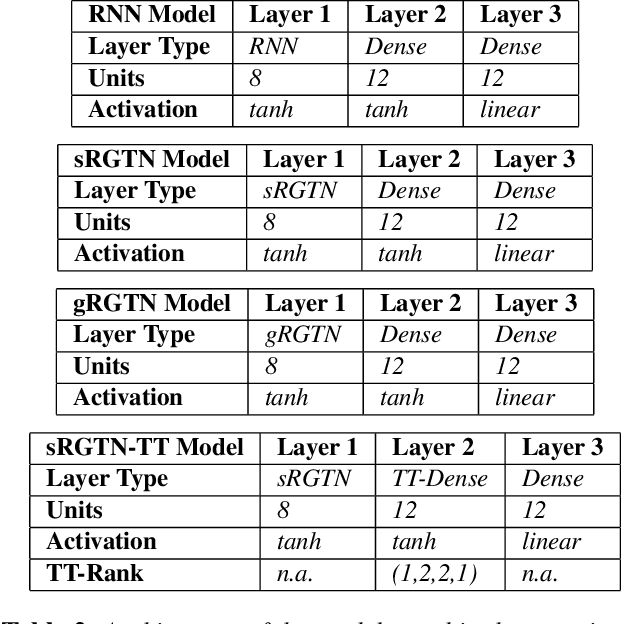
Abstract:Recurrent Neural Networks (RNNs) are among the most successful machine learning models for sequence modelling. In this paper, we show that the modelling of hidden states in RNNs can be approximated through a multi-linear graph filter, which describes the directional flow of temporal information. The so derived multi-linear graph filter is then generalized to a tensor network form to improve its modelling power, resulting in a novel Recurrent Graph Tensor Network (RGTN). To validate the expressive power of the derived network, several variants of RGTN models were proposed and employed for the task of time-series forecasting, demonstrating superior properties in terms of convergence, performance, and complexity. By leveraging the multi-modal nature of tensor networks, RGTN models were shown to out-perform a standard RNN by 23% in terms of mean-squared-error while using up to 86% less parameters. Therefore, by combining the expressive power of tensor networks with a suitable graph filter, we show that the proposed RGTN models can out-perform a classical RNN at a drastically lower parameter complexity, especially in the multi-modal setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge