Graph Tensor Networks: An Intuitive Framework for Designing Large-Scale Neural Learning Systems on Multiple Domains

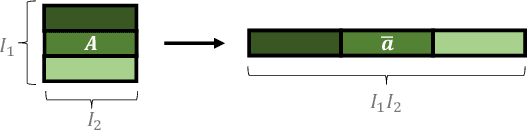
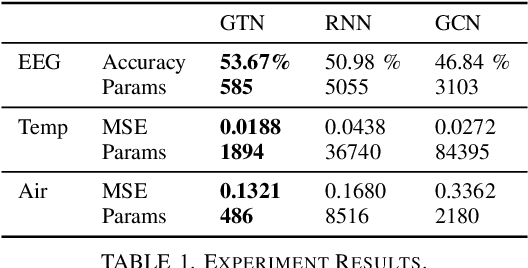
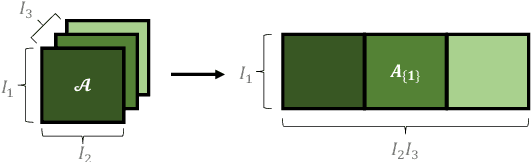
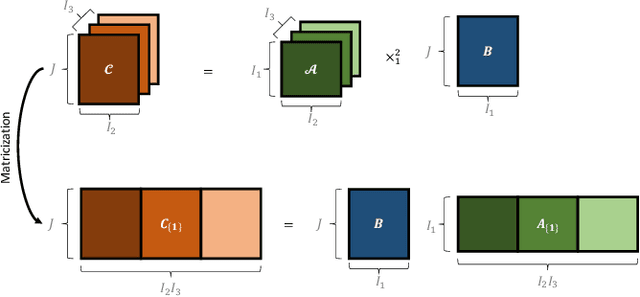
Despite the omnipresence of tensors and tensor operations in modern deep learning, the use of tensor mathematics to formally design and describe neural networks is still under-explored within the deep learning community. To this end, we introduce the Graph Tensor Network (GTN) framework, an intuitive yet rigorous graphical framework for systematically designing and implementing large-scale neural learning systems on both regular and irregular domains. The proposed framework is shown to be general enough to include many popular architectures as special cases, and flexible enough to handle data on any and many data domains. The power and flexibility of the proposed framework is demonstrated through real-data experiments, resulting in improved performance at a drastically lower complexity costs, by virtue of tensor algebra.

Graph-Regularized Tensor Regression: A Domain-Aware Framework for Interpretable Multi-Way Financial Modelling

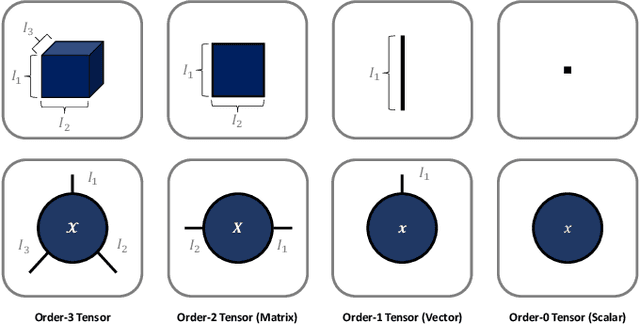
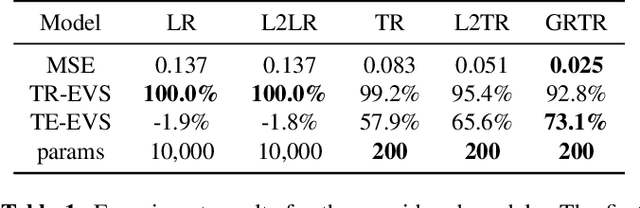
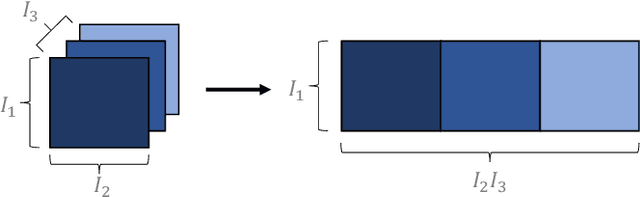
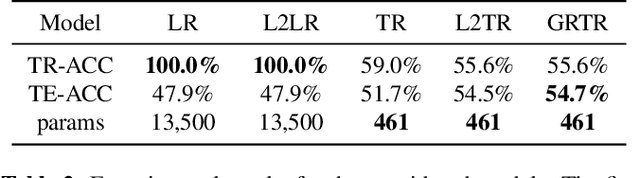
Analytics of financial data is inherently a Big Data paradigm, as such data are collected over many assets, asset classes, countries, and time periods. This represents a challenge for modern machine learning models, as the number of model parameters needed to process such data grows exponentially with the data dimensions; an effect known as the Curse-of-Dimensionality. Recently, Tensor Decomposition (TD) techniques have shown promising results in reducing the computational costs associated with large-dimensional financial models while achieving comparable performance. However, tensor models are often unable to incorporate the underlying economic domain knowledge. To this end, we develop a novel Graph-Regularized Tensor Regression (GRTR) framework, whereby knowledge about cross-asset relations is incorporated into the model in the form of a graph Laplacian matrix. This is then used as a regularization tool to promote an economically meaningful structure within the model parameters. By virtue of tensor algebra, the proposed framework is shown to be fully interpretable, both coefficient-wise and dimension-wise. The GRTR model is validated in a multi-way financial forecasting setting and compared against competing models, and is shown to achieve improved performance at reduced computational costs. Detailed visualizations are provided to help the reader gain an intuitive understanding of the employed tensor operations.

Tensor Networks for Multi-Modal Non-Euclidean Data

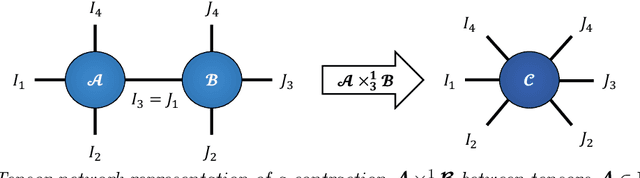
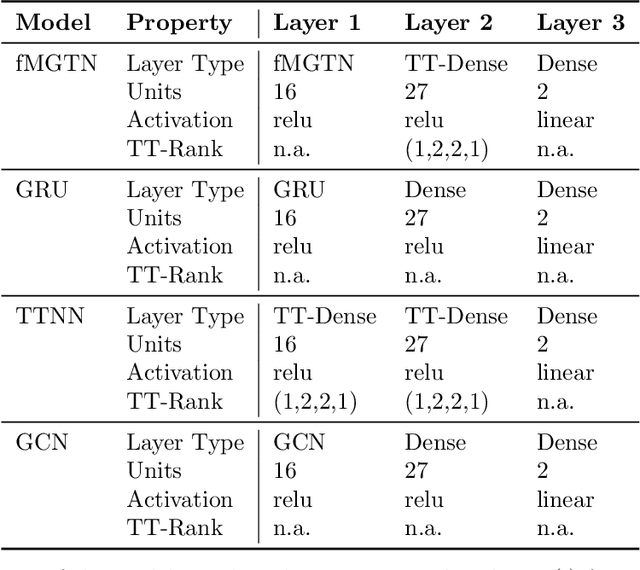
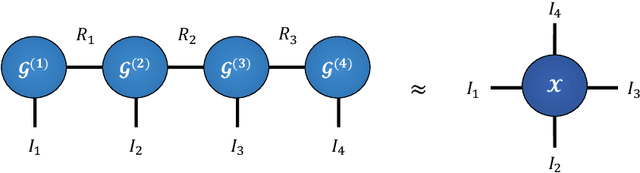
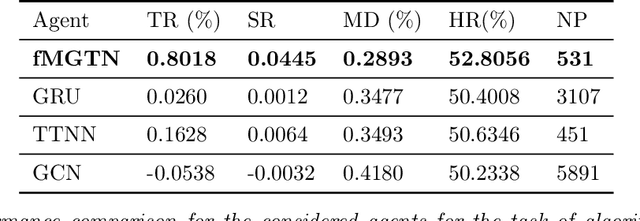
Modern data sources are typically of large scale and multi-modal natures, and acquired on irregular domains, which poses serious challenges to traditional deep learning models. These issues are partially mitigated by either extending existing deep learning algorithms to irregular domains through graphs, or by employing tensor methods to alleviate the computational bottlenecks imposed by the Curse of Dimensionality. To simultaneously resolve both these issues, we introduce a novel Multi-Graph Tensor Network (MGTN) framework, which leverages on the desirable properties of graphs, tensors and neural networks in a physically meaningful and compact manner. This equips MGTNs with the ability to exploit local information in irregular data sources at a drastically reduced parameter complexity, and over a range of learning paradigms such as regression, classification and reinforcement learning. The benefits of the MGTN framework, especially its ability to avoid overfitting through the inherent low-rank regularization properties of tensor networks, are demonstrated through its superior performance against competing models in the individual tensor, graph, and neural network domains.

Multi-Graph Tensor Networks

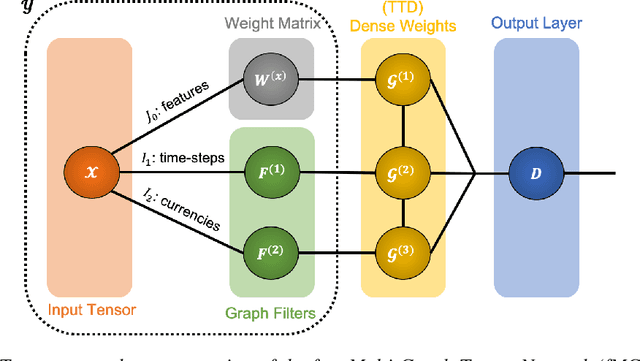
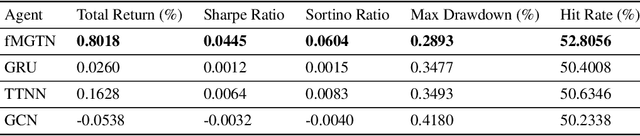
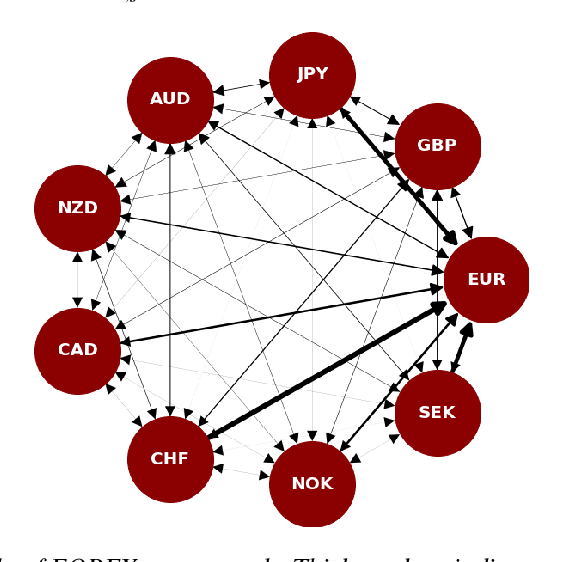
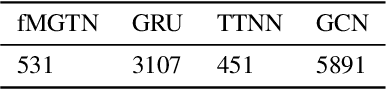
The irregular and multi-modal nature of numerous modern data sources poses serious challenges for traditional deep learning algorithms. To this end, recent efforts have generalized existing algorithms to irregular domains through graphs, with the aim to gain additional insights from data through the underlying graph topology. At the same time, tensor-based methods have demonstrated promising results in bypassing the bottlenecks imposed by the Curse of Dimensionality. In this paper, we introduce a novel Multi-Graph Tensor Network (MGTN) framework, which exploits both the ability of graphs to handle irregular data sources and the compression properties of tensor networks in a deep learning setting. The potential of the proposed framework is demonstrated through an MGTN based deep Q agent for Foreign Exchange (FOREX) algorithmic trading. By virtue of the MGTN, a FOREX currency graph is leveraged to impose an economically meaningful structure on this demanding task, resulting in a highly superior performance against three competing models and at a drastically lower complexity.

Supervised Learning for Non-Sequential Data with the Canonical Polyadic Decomposition

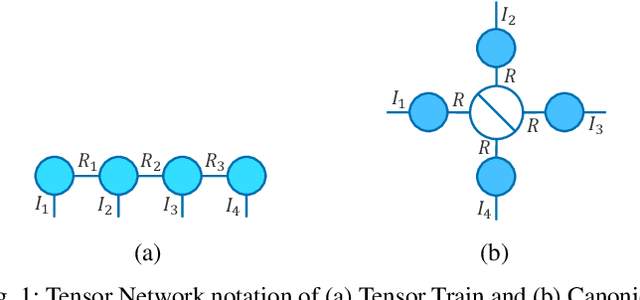
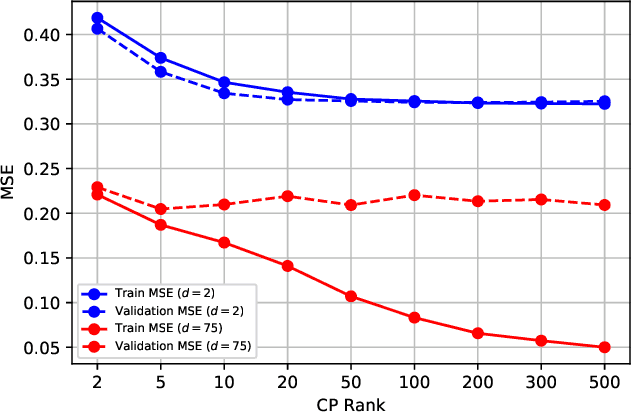
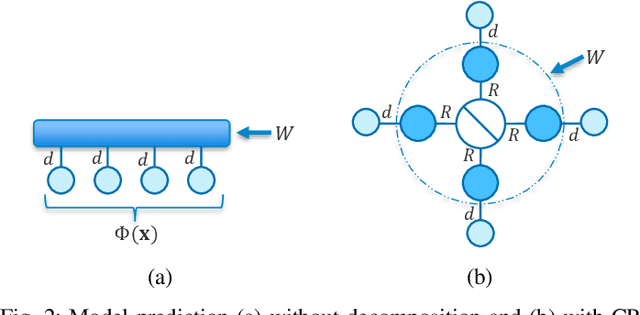
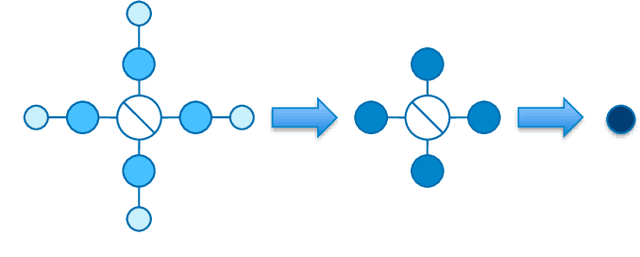
There has recently been increasing interest, both theoretical and practical, in utilizing tensor networks for the analysis and design of machine learning systems. In particular, a framework has been proposed that can handle both dense data (e.g., standard regression or classification tasks) and sparse data (e.g., recommender systems), unlike support vector machines and traditional deep learning techniques. Namely, it can be interpreted as applying local feature mappings to the data and, through the outer product operator, modelling all interactions of functions of the features; the corresponding weights are represented as a tensor network for computational tractability. In this paper, we derive efficient prediction and learning algorithms for supervised learning with the Canonical Polyadic (CP) decomposition, including suitable regularization and initialization schemes. We empirically demonstrate that the CP-based model performs at least on par with the existing models based on the Tensor Train (TT) decomposition on standard non-sequential tasks, and better on MovieLens 100K. Furthermore, in contrast to previous works which applied two-dimensional local feature maps to the data, we generalize the framework to handle arbitrarily high-dimensional maps, in order to gain a powerful lever on the expressiveness of the model. In order to enhance its stability and generalization capabilities, we propose a normalized version of the feature maps. Our experiments show that this version leads to dramatic improvements over the unnormalized and/or two-dimensional maps, as well as to performance on non-sequential supervised learning tasks that compares favourably with popular models, including neural networks.