Supervised Learning for Non-Sequential Data with the Canonical Polyadic Decomposition

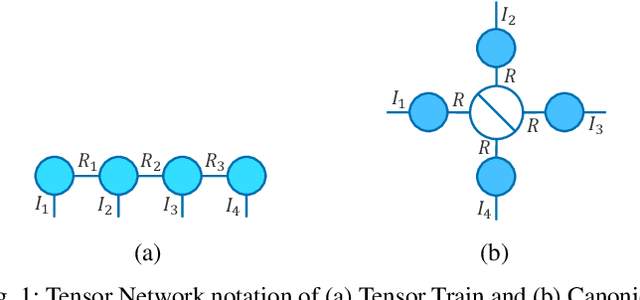
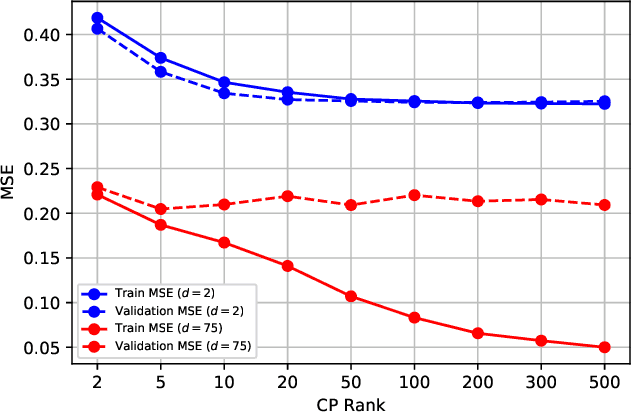
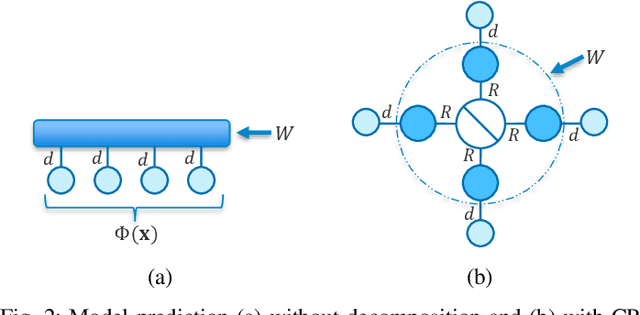
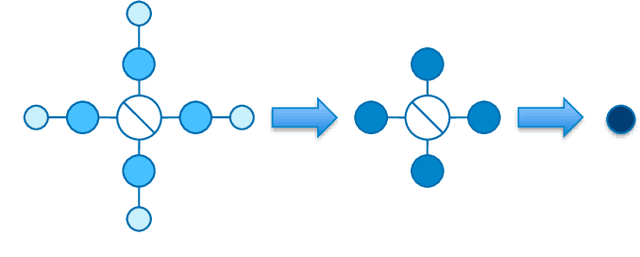
There has recently been increasing interest, both theoretical and practical, in utilizing tensor networks for the analysis and design of machine learning systems. In particular, a framework has been proposed that can handle both dense data (e.g., standard regression or classification tasks) and sparse data (e.g., recommender systems), unlike support vector machines and traditional deep learning techniques. Namely, it can be interpreted as applying local feature mappings to the data and, through the outer product operator, modelling all interactions of functions of the features; the corresponding weights are represented as a tensor network for computational tractability. In this paper, we derive efficient prediction and learning algorithms for supervised learning with the Canonical Polyadic (CP) decomposition, including suitable regularization and initialization schemes. We empirically demonstrate that the CP-based model performs at least on par with the existing models based on the Tensor Train (TT) decomposition on standard non-sequential tasks, and better on MovieLens 100K. Furthermore, in contrast to previous works which applied two-dimensional local feature maps to the data, we generalize the framework to handle arbitrarily high-dimensional maps, in order to gain a powerful lever on the expressiveness of the model. In order to enhance its stability and generalization capabilities, we propose a normalized version of the feature maps. Our experiments show that this version leads to dramatic improvements over the unnormalized and/or two-dimensional maps, as well as to performance on non-sequential supervised learning tasks that compares favourably with popular models, including neural networks.