Tensor-Train Recurrent Neural Networks for Interpretable Multi-Way Financial Forecasting
Paper and Code
May 11, 2021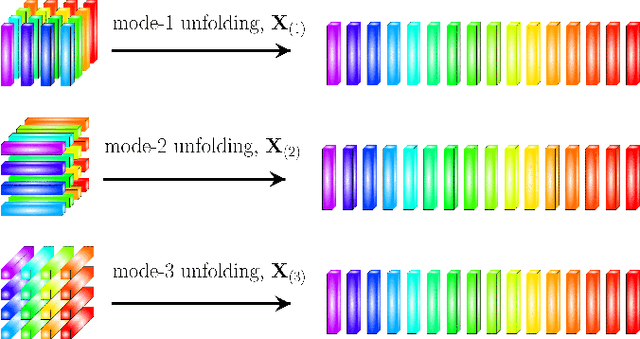
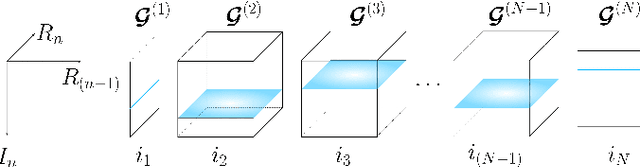

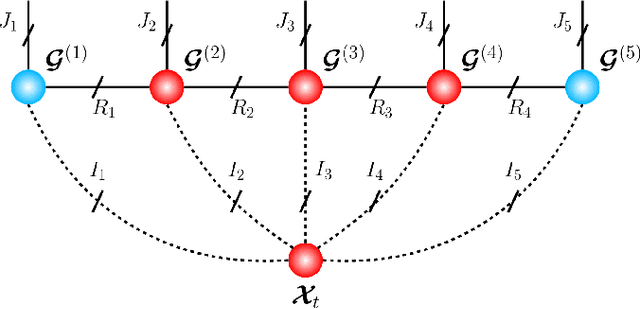
Recurrent Neural Networks (RNNs) represent the de facto standard machine learning tool for sequence modelling, owing to their expressive power and memory. However, when dealing with large dimensional data, the corresponding exponential increase in the number of parameters imposes a computational bottleneck. The necessity to equip RNNs with the ability to deal with the curse of dimensionality, such as through the parameter compression ability inherent to tensors, has led to the development of the Tensor-Train RNN (TT-RNN). Despite achieving promising results in many applications, the full potential of the TT-RNN is yet to be explored in the context of interpretable financial modelling, a notoriously challenging task characterized by multi-modal data with low signal-to-noise ratio. To address this issue, we investigate the potential of TT-RNN in the task of financial forecasting of currencies. We show, through the analysis of TT-factors, that the physical meaning underlying tensor decomposition, enables the TT-RNN model to aid the interpretability of results, thus mitigating the notorious "black-box" issue associated with neural networks. Furthermore, simulation results highlight the regularization power of TT decomposition, demonstrating the superior performance of TT-RNN over its uncompressed RNN counterpart and other tensor forecasting methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge