Giuseppe G. Calvi
HOTTBOX: Higher Order Tensor ToolBOX
Nov 30, 2021
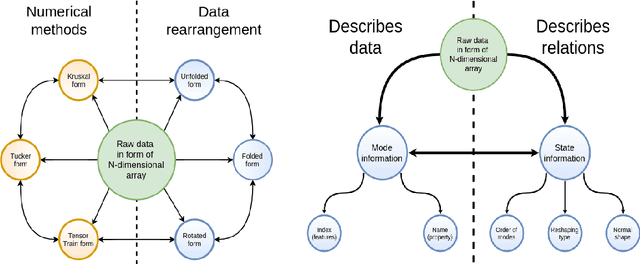
Abstract:HOTTBOX is a Python library for exploratory analysis and visualisation of multi-dimensional arrays of data, also known as tensors. The library includes methods ranging from standard multi-way operations and data manipulation through to multi-linear algebra based tensor decompositions. HOTTBOX also comprises sophisticated algorithms for generalised multi-linear classification and data fusion, such as Support Tensor Machine (STM) and Tensor Ensemble Learning (TEL). For user convenience, HOTTBOX offers a unifying API which establishes a self-sufficient ecosystem for various forms of efficient representation of multi-way data and the corresponding decomposition and association algorithms. Particular emphasis is placed on scalability and interactive visualisation, to support multidisciplinary data analysis communities working on big data and tensors. HOTTBOX also provides means for integration with other popular data science libraries for visualisation and data manipulation. The source code, examples and documentation ca be found at https://github.com/hottbox/hottbox.
Tensor-Train Recurrent Neural Networks for Interpretable Multi-Way Financial Forecasting
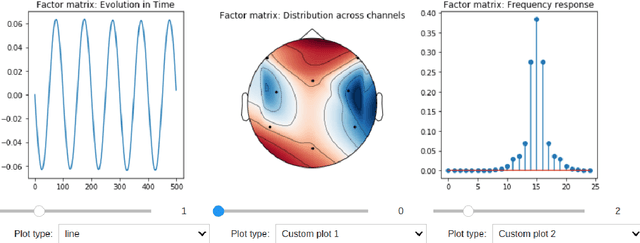
May 11, 2021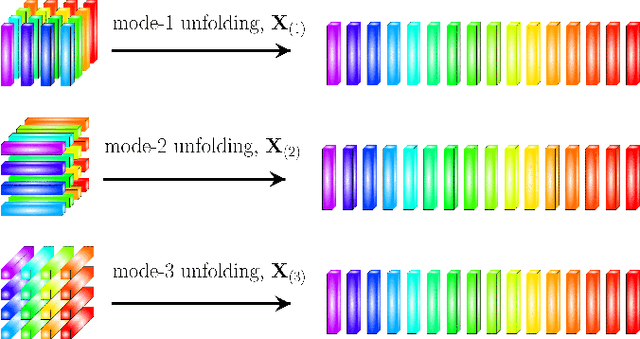
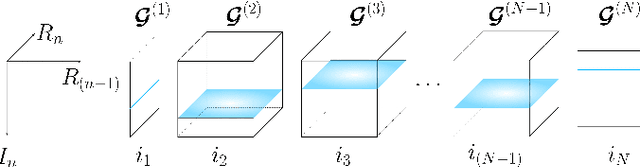

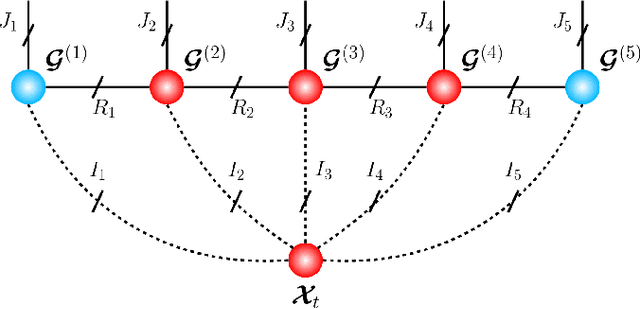
Abstract:Recurrent Neural Networks (RNNs) represent the de facto standard machine learning tool for sequence modelling, owing to their expressive power and memory. However, when dealing with large dimensional data, the corresponding exponential increase in the number of parameters imposes a computational bottleneck. The necessity to equip RNNs with the ability to deal with the curse of dimensionality, such as through the parameter compression ability inherent to tensors, has led to the development of the Tensor-Train RNN (TT-RNN). Despite achieving promising results in many applications, the full potential of the TT-RNN is yet to be explored in the context of interpretable financial modelling, a notoriously challenging task characterized by multi-modal data with low signal-to-noise ratio. To address this issue, we investigate the potential of TT-RNN in the task of financial forecasting of currencies. We show, through the analysis of TT-factors, that the physical meaning underlying tensor decomposition, enables the TT-RNN model to aid the interpretability of results, thus mitigating the notorious "black-box" issue associated with neural networks. Furthermore, simulation results highlight the regularization power of TT decomposition, demonstrating the superior performance of TT-RNN over its uncompressed RNN counterpart and other tensor forecasting methods.
Tucker Tensor Layer in Fully Connected Neural Networks
Mar 14, 2019
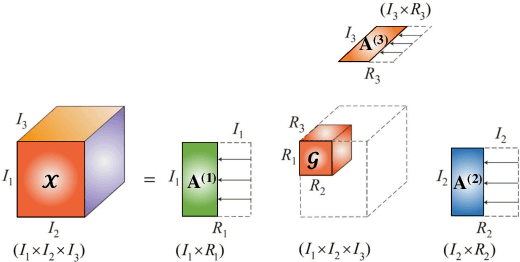

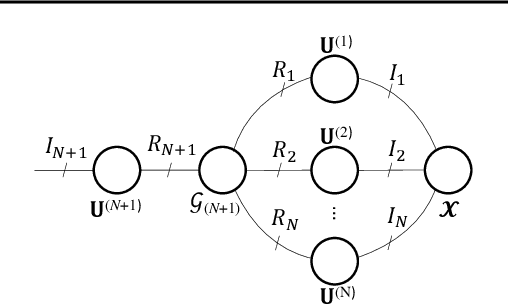
Abstract:We introduce the Tucker Tensor Layer (TTL), an alternative to the dense weight-matrices of the fully connected layers of feed-forward neural networks (NNs), to answer the long standing quest to compress NNs and improve their interpretability. This is achieved by treating these weight-matrices as the unfolding of a higher order weight-tensor. This enables us to introduce a framework for exploiting the multi-way nature of the weight-tensor in order to efficiently reduce the number of parameters, by virtue of the compression properties of tensor decompositions. The Tucker Decomposition (TKD) is employed to decompose the weight-tensor into a core tensor and factor matrices. We re-derive back-propagation within this framework, by extending the notion of matrix derivatives to tensors. In this way, the physical interpretability of the TKD is exploited to gain insights into training, through the process of computing gradients with respect to each factor matrix. The proposed framework is validated on synthetic data and on the Fashion-MNIST dataset, emphasizing the relative importance of various data features in training, hence mitigating the "black-box" issue inherent to NNs. Experiments on both MNIST and Fashion-MNIST illustrate the compression properties of the TTL, achieving a 66.63 fold compression whilst maintaining comparable performance to the uncompressed NN.
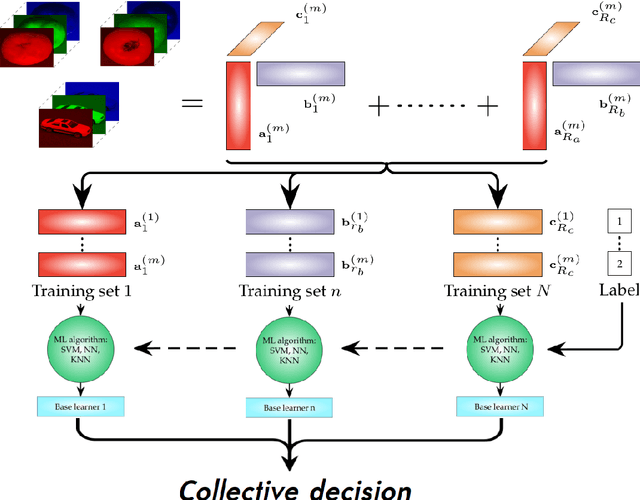
Tensor Valued Common and Individual Feature Extraction: Multi-dimensional Perspective
Nov 01, 2017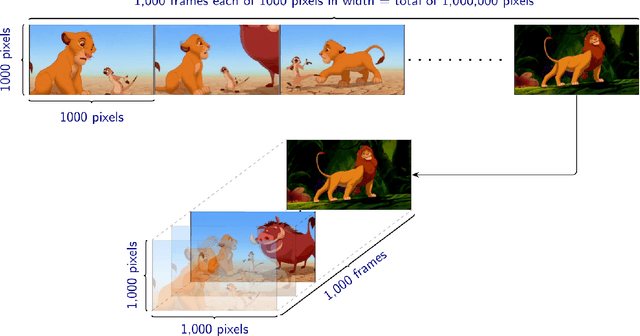
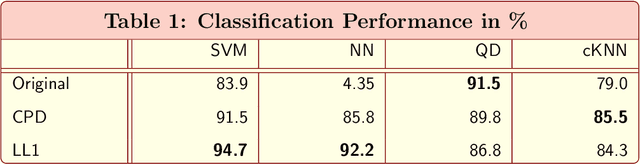
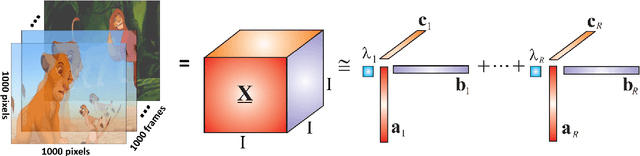

Abstract:A novel method for common and individual feature analysis from exceedingly large-scale data is proposed, in order to ensure the tractability of both the computation and storage and thus mitigate the curse of dimensionality, a major bottleneck in modern data science. This is achieved by making use of the inherent redundancy in so-called multi-block data structures, which represent multiple observations of the same phenomenon taken at different times, angles or recording conditions. Upon providing an intrinsic link between the properties of the outer vector product and extracted features in tensor decompositions (TDs), the proposed common and individual information extraction from multi-block data is performed through imposing physical meaning to otherwise unconstrained factorisation approaches. This is shown to dramatically reduce the dimensionality of search spaces for subsequent classification procedures and to yield greatly enhanced accuracy. Simulations on a multi-class classification task of large-scale extraction of individual features from a collection of partially related real-world images demonstrate the advantages of the "blessing of dimensionality" associated with TDs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge