Deep learning framework for crater detection and identification on the Moon and Mars

Impact craters are among the most prominent geomorphological features on planetary surfaces and are of substantial significance in planetary science research. Their spatial distribution and morphological characteristics provide critical information on planetary surface composition, geological history, and impact processes. In recent years, the rapid advancement of deep learning models has fostered significant interest in automated crater detection. In this paper, we apply advancements in deep learning models for impact crater detection and identification. We use novel models, including Convolutional Neural Networks (CNNs) and variants such as YOLO and ResNet. We present a framework that features a two-stage approach where the first stage features crater identification using simple classic CNN, ResNet-50 and YOLO. In the second stage, our framework employs YOLO-based detection for crater localisation. Therefore, we detect and identify different types of craters and present a summary report with remote sensing data for a selected region. We consider selected regions for craters and identification from Mars and the Moon based on remote sensing data. Our results indicate that YOLO demonstrates the most balanced crater detection performance, while ResNet-50 excels in identifying large craters with high precision.

Reciprocal Adversarial Learning via Characteristic Functions

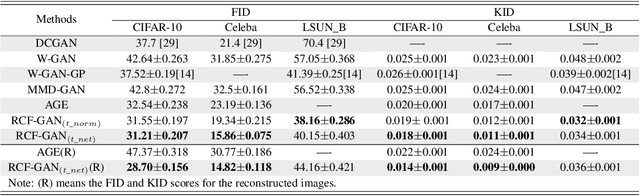
Generative adversarial nets (GANs) have become a preferred tool for accommodating complicated distributions, and to stabilise the training and reduce the mode collapse of GANs, one of their main variants employs the integral probability metric (IPM) as the loss function. Although theoretically supported, extensive IPM-GANs are basically comparing moments in an embedded domain of the \textit{critic}. We generalise this by comparing the distributions rather than the moments via a powerful tool, i.e., the characteristic function (CF), which uniquely and universally contains all the information about a distribution. For rigour, we first establish the physical meaning of the phase and amplitude in CFs. This provides a feasible way of manipulating the generation. We then develop an efficient sampling way to calculate the CFs. Within this framework, we further prove an equivalence between the embedded and data domains when a reciprocal exists, which allows us to develop the GAN in an auto-encoder way, by using only two modules to achieve bi-directionally generating clear images. We refer to this efficient structure as the reciprocal CF GAN (RCF-GAN). Experimental results show the superior performances of the proposed RCF-GAN in terms of both generation and reconstruction.

A general solver to the elliptical mixture model through an approximate Wasserstein manifold

This paper studies the problem of estimation for general finite mixture models, with a particular focus on the elliptical mixture models (EMMs). Instead of using the widely adopted Kullback-Leibler divergence, we provide a stable solution to the EMMs that is robust to initialisations and attains superior local optimum by adaptively optimising along a manifold of an approximate Wasserstein distance. More specifically, we first summarise computable and identifiable EMMs, in order to identify the optimisation problem. Due to a probability constraint, solving this problem is cumbersome and unstable, especially under the Wasserstein distance. We thus resort to an efficient optimisation on a statistical manifold defined under an approximate Wasserstein distance, which allows for explicit metrics and operations. This is shown to significantly stabilise and improve the EMM estimations. We also propose an adaptive method to further accelerate the convergence. Experimental results demonstrate excellent performances of the proposed solver.

Tucker Tensor Layer in Fully Connected Neural Networks

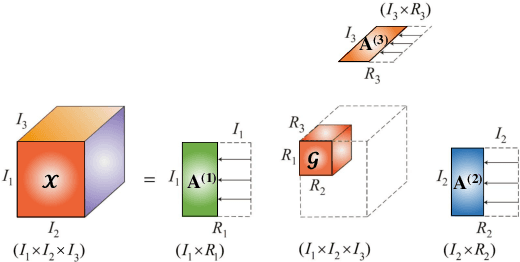
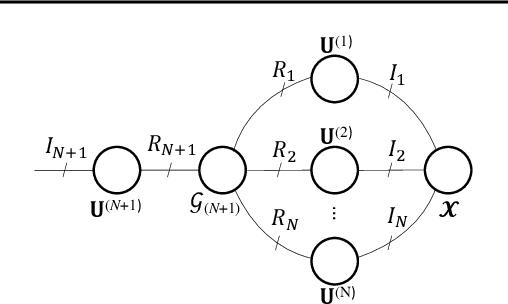
We introduce the Tucker Tensor Layer (TTL), an alternative to the dense weight-matrices of the fully connected layers of feed-forward neural networks (NNs), to answer the long standing quest to compress NNs and improve their interpretability. This is achieved by treating these weight-matrices as the unfolding of a higher order weight-tensor. This enables us to introduce a framework for exploiting the multi-way nature of the weight-tensor in order to efficiently reduce the number of parameters, by virtue of the compression properties of tensor decompositions. The Tucker Decomposition (TKD) is employed to decompose the weight-tensor into a core tensor and factor matrices. We re-derive back-propagation within this framework, by extending the notion of matrix derivatives to tensors. In this way, the physical interpretability of the TKD is exploited to gain insights into training, through the process of computing gradients with respect to each factor matrix. The proposed framework is validated on synthetic data and on the Fashion-MNIST dataset, emphasizing the relative importance of various data features in training, hence mitigating the "black-box" issue inherent to NNs. Experiments on both MNIST and Fashion-MNIST illustrate the compression properties of the TTL, achieving a 66.63 fold compression whilst maintaining comparable performance to the uncompressed NN.

Widely Linear Complex-valued Autoencoder: Dealing with Noncircularity in Generative-Discriminative Models

We propose a new structure for the complex-valued autoencoder by introducing additional degrees of freedom into its design through a widely linear (WL) transform. The corresponding widely linear backpropagation algorithm is also developed using the $\mathbb{CR}$ calculus, to unify the gradient calculation of the cost function and the underlying WL model. More specifically, all the existing complex-valued autoencoders employ the strictly linear transform, which is optimal only when the complex-valued outputs of each network layer are independent of the conjugate of the inputs. In addition, the widely linear model which underpins our work allows us to consider all the second-order statistics of inputs. This provides more freedom in the design and enhanced optimization opportunities, as compared to the state-of-the-art. Furthermore, we show that the most widely adopted cost function, i.e., the mean squared error, is not best suited for the complex domain, as it is a real quantity with a single degree of freedom, while both the phase and the amplitude information need to be optimized. To resolve this issue, we design a new cost function, which is capable of controlling the balance between the phase and the amplitude contribution to the solution. The experimental results verify the superior performance of the proposed autoencoder together with the new cost function, especially for the imaging scenarios where the phase preserves extensive information on edges and shapes.

Artificial Intelligence for Prosthetics - challenge solutions

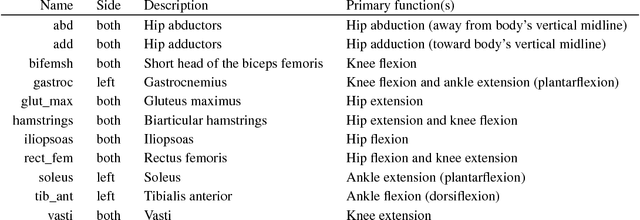
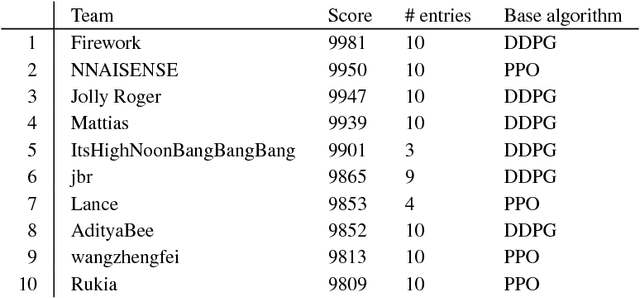
In the NeurIPS 2018 Artificial Intelligence for Prosthetics challenge, participants were tasked with building a controller for a musculoskeletal model with a goal of matching a given time-varying velocity vector. Top participants were invited to describe their algorithms. In this work, we describe the challenge and present thirteen solutions that used deep reinforcement learning approaches. Many solutions use similar relaxations and heuristics, such as reward shaping, frame skipping, discretization of the action space, symmetry, and policy blending. However, each team implemented different modifications of the known algorithms by, for example, dividing the task into subtasks, learning low-level control, or by incorporating expert knowledge and using imitation learning.

A universal framework for learning based on the elliptical mixture model

An increasing prominence of unbalanced and noisy data highlights the importance of elliptical mixture models (EMMs), which exhibit enhanced robustness, flexibility and stability over the widely applied Gaussian mixture model (GMM). However, existing studies of the EMM are typically of \textit{ad hoc} nature, without a universal analysis framework or existence and uniqueness considerations. To this end, we propose a general framework for estimating the EMM, which makes use of the Riemannian manifold optimisation to convert the original constrained optimisation paradigms into an un-constrained one. We first revisit the statistics of elliptical distributions, to give a rationale for the use of Riemannian metrics as well as the reformulation of the problem in the Riemannian space. We then derive the EMM learning framework, based on Riemannian gradient descent, which ensures the same optimum as the original problem but accelerates the convergence speed. We also unify the treatment of the existing elliptical distributions to build a universal EMM, providing a simple and intuitive way to deal with the non-convex nature of this optimisation problem. Numerical results demonstrate the ability of the proposed framework to accommodate EMMs with different properties of individual functions, and also verify the robustness and flexibility of the proposed framework over the standard GMM.