Reciprocal Adversarial Learning via Characteristic Functions

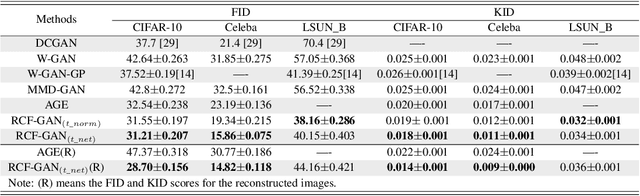
Generative adversarial nets (GANs) have become a preferred tool for accommodating complicated distributions, and to stabilise the training and reduce the mode collapse of GANs, one of their main variants employs the integral probability metric (IPM) as the loss function. Although theoretically supported, extensive IPM-GANs are basically comparing moments in an embedded domain of the \textit{critic}. We generalise this by comparing the distributions rather than the moments via a powerful tool, i.e., the characteristic function (CF), which uniquely and universally contains all the information about a distribution. For rigour, we first establish the physical meaning of the phase and amplitude in CFs. This provides a feasible way of manipulating the generation. We then develop an efficient sampling way to calculate the CFs. Within this framework, we further prove an equivalence between the embedded and data domains when a reciprocal exists, which allows us to develop the GAN in an auto-encoder way, by using only two modules to achieve bi-directionally generating clear images. We refer to this efficient structure as the reciprocal CF GAN (RCF-GAN). Experimental results show the superior performances of the proposed RCF-GAN in terms of both generation and reconstruction.