Causal Context Adjustment Loss for Learned Image Compression

In recent years, learned image compression (LIC) technologies have surpassed conventional methods notably in terms of rate-distortion (RD) performance. Most present learned techniques are VAE-based with an autoregressive entropy model, which obviously promotes the RD performance by utilizing the decoded causal context. However, extant methods are highly dependent on the fixed hand-crafted causal context. The question of how to guide the auto-encoder to generate a more effective causal context benefit for the autoregressive entropy models is worth exploring. In this paper, we make the first attempt in investigating the way to explicitly adjust the causal context with our proposed Causal Context Adjustment loss (CCA-loss). By imposing the CCA-loss, we enable the neural network to spontaneously adjust important information into the early stage of the autoregressive entropy model. Furthermore, as transformer technology develops remarkably, variants of which have been adopted by many state-of-the-art (SOTA) LIC techniques. The existing computing devices have not adapted the calculation of the attention mechanism well, which leads to a burden on computation quantity and inference latency. To overcome it, we establish a convolutional neural network (CNN) image compression model and adopt the unevenly channel-wise grouped strategy for high efficiency. Ultimately, the proposed CNN-based LIC network trained with our Causal Context Adjustment loss attains a great trade-off between inference latency and rate-distortion performance.

QVD: Post-training Quantization for Video Diffusion Models

Recently, video diffusion models (VDMs) have garnered significant attention due to their notable advancements in generating coherent and realistic video content. However, processing multiple frame features concurrently, coupled with the considerable model size, results in high latency and extensive memory consumption, hindering their broader application. Post-training quantization (PTQ) is an effective technique to reduce memory footprint and improve computational efficiency. Unlike image diffusion, we observe that the temporal features, which are integrated into all frame features, exhibit pronounced skewness. Furthermore, we investigate significant inter-channel disparities and asymmetries in the activation of video diffusion models, resulting in low coverage of quantization levels by individual channels and increasing the challenge of quantization. To address these issues, we introduce the first PTQ strategy tailored for video diffusion models, dubbed QVD. Specifically, we propose the High Temporal Discriminability Quantization (HTDQ) method, designed for temporal features, which retains the high discriminability of quantized features, providing precise temporal guidance for all video frames. In addition, we present the Scattered Channel Range Integration (SCRI) method which aims to improve the coverage of quantization levels across individual channels. Experimental validations across various models, datasets, and bit-width settings demonstrate the effectiveness of our QVD in terms of diverse metrics. In particular, we achieve near-lossless performance degradation on W8A8, outperforming the current methods by 205.12 in FVD.

Blind Super-Resolution via Meta-learning and Markov Chain Monte Carlo Simulation

Learning-based approaches have witnessed great successes in blind single image super-resolution (SISR) tasks, however, handcrafted kernel priors and learning based kernel priors are typically required. In this paper, we propose a Meta-learning and Markov Chain Monte Carlo (MCMC) based SISR approach to learn kernel priors from organized randomness. In concrete, a lightweight network is adopted as kernel generator, and is optimized via learning from the MCMC simulation on random Gaussian distributions. This procedure provides an approximation for the rational blur kernel, and introduces a network-level Langevin dynamics into SISR optimization processes, which contributes to preventing bad local optimal solutions for kernel estimation. Meanwhile, a meta-learning-based alternating optimization procedure is proposed to optimize the kernel generator and image restorer, respectively. In contrast to the conventional alternating minimization strategy, a meta-learning-based framework is applied to learn an adaptive optimization strategy, which is less-greedy and results in better convergence performance. These two procedures are iteratively processed in a plug-and-play fashion, for the first time, realizing a learning-based but plug-and-play blind SISR solution in unsupervised inference. Extensive simulations demonstrate the superior performance and generalization ability of the proposed approach when comparing with state-of-the-arts on synthesis and real-world datasets. The code is available at https://github.com/XYLGroup/MLMC.

A Dynamic Kernel Prior Model for Unsupervised Blind Image Super-Resolution

Deep learning-based methods have achieved significant successes on solving the blind super-resolution (BSR) problem. However, most of them request supervised pre-training on labelled datasets. This paper proposes an unsupervised kernel estimation model, named dynamic kernel prior (DKP), to realize an unsupervised and pre-training-free learning-based algorithm for solving the BSR problem. DKP can adaptively learn dynamic kernel priors to realize real-time kernel estimation, and thereby enables superior HR image restoration performances. This is achieved by a Markov chain Monte Carlo sampling process on random kernel distributions. The learned kernel prior is then assigned to optimize a blur kernel estimation network, which entails a network-based Langevin dynamic optimization strategy. These two techniques ensure the accuracy of the kernel estimation. DKP can be easily used to replace the kernel estimation models in the existing methods, such as Double-DIP and FKP-DIP, or be added to the off-the-shelf image restoration model, such as diffusion model. In this paper, we incorporate our DKP model with DIP and diffusion model, referring to DIP-DKP and Diff-DKP, for validations. Extensive simulations on Gaussian and motion kernel scenarios demonstrate that the proposed DKP model can significantly improve the kernel estimation with comparable runtime and memory usage, leading to state-of-the-art BSR results. The code is available at https://github.com/XYLGroup/DKP.

Enhancing Quality of Compressed Images by Mitigating Enhancement Bias Towards Compression Domain

Existing quality enhancement methods for compressed images focus on aligning the enhancement domain with the raw domain to yield realistic images. However, these methods exhibit a pervasive enhancement bias towards the compression domain, inadvertently regarding it as more realistic than the raw domain. This bias makes enhanced images closely resemble their compressed counterparts, thus degrading their perceptual quality. In this paper, we propose a simple yet effective method to mitigate this bias and enhance the quality of compressed images. Our method employs a conditional discriminator with the compressed image as a key condition, and then incorporates a domain-divergence regularization to actively distance the enhancement domain from the compression domain. Through this dual strategy, our method enables the discrimination against the compression domain, and brings the enhancement domain closer to the raw domain. Comprehensive quality evaluations confirm the superiority of our method over other state-of-the-art methods without incurring inference overheads.

Demystifying CNNs for Images by Matched Filters

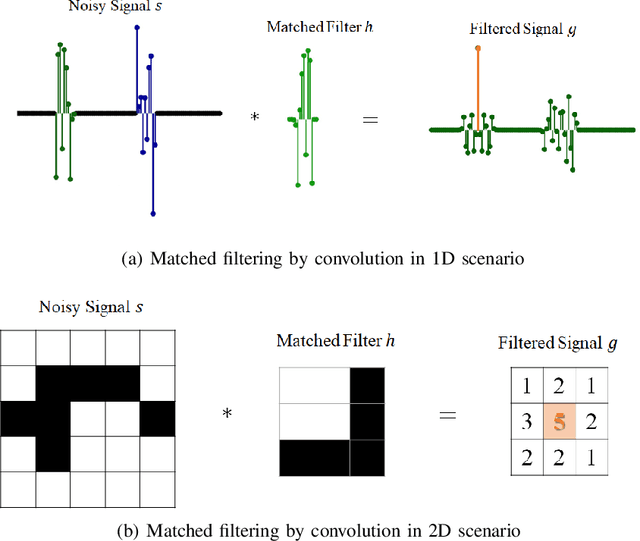
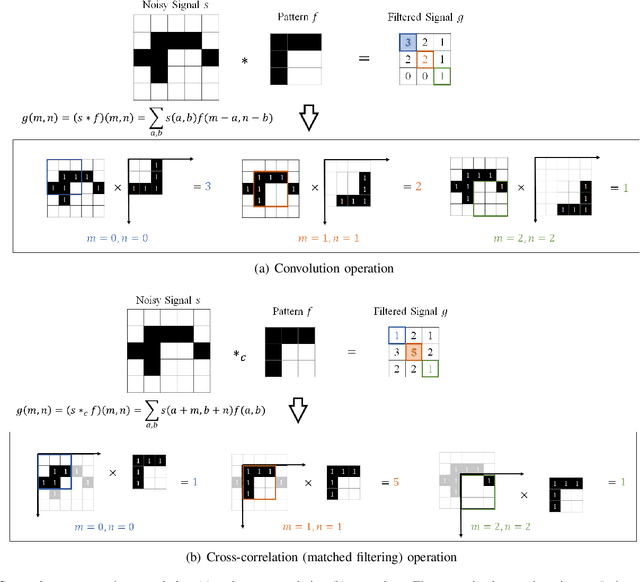
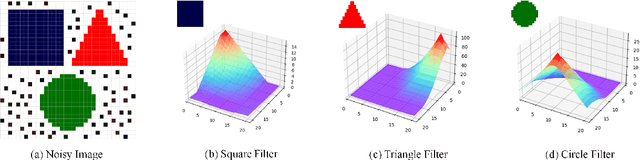
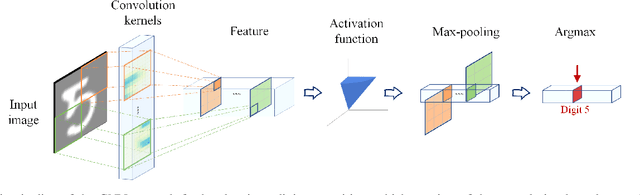
The success of convolution neural networks (CNN) has been revolutionising the way we approach and use intelligent machines in the Big Data era. Despite success, CNNs have been consistently put under scrutiny owing to their \textit{black-box} nature, an \textit{ad hoc} manner of their construction, together with the lack of theoretical support and physical meanings of their operation. This has been prohibitive to both the quantitative and qualitative understanding of CNNs, and their application in more sensitive areas such as AI for health. We set out to address these issues, and in this way demystify the operation of CNNs, by employing the perspective of matched filtering. We first illuminate that the convolution operation, the very core of CNNs, represents a matched filter which aims to identify the presence of features in input data. This then serves as a vehicle to interpret the convolution-activation-pooling chain in CNNs under the theoretical umbrella of matched filtering, a common operation in signal processing. We further provide extensive examples and experiments to illustrate this connection, whereby the learning in CNNs is shown to also perform matched filtering, which further sheds light onto physical meaning of learnt parameters and layers. It is our hope that this material will provide new insights into the understanding, constructing and analysing of CNNs, as well as paving the way for developing new methods and architectures of CNNs.

Blind VQA on 360° Video via Progressively Learning from Pixels, Frames and Video

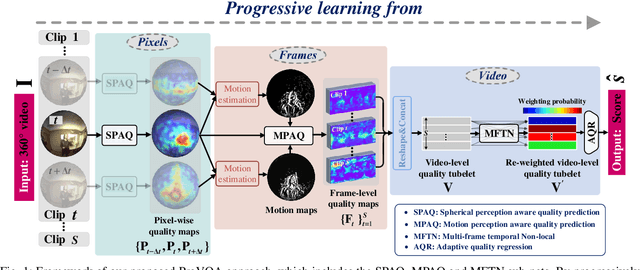
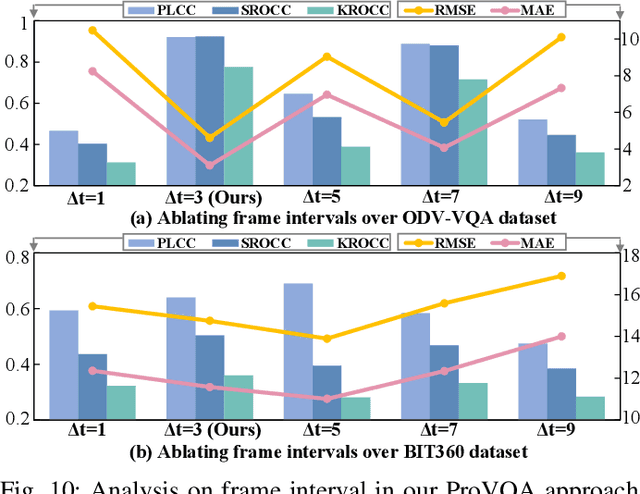
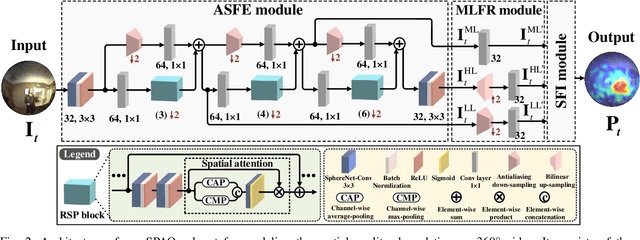
Blind visual quality assessment (BVQA) on 360{\textdegree} video plays a key role in optimizing immersive multimedia systems. When assessing the quality of 360{\textdegree} video, human tends to perceive its quality degradation from the viewport-based spatial distortion of each spherical frame to motion artifact across adjacent frames, ending with the video-level quality score, i.e., a progressive quality assessment paradigm. However, the existing BVQA approaches for 360{\textdegree} video neglect this paradigm. In this paper, we take into account the progressive paradigm of human perception towards spherical video quality, and thus propose a novel BVQA approach (namely ProVQA) for 360{\textdegree} video via progressively learning from pixels, frames and video. Corresponding to the progressive learning of pixels, frames and video, three sub-nets are designed in our ProVQA approach, i.e., the spherical perception aware quality prediction (SPAQ), motion perception aware quality prediction (MPAQ) and multi-frame temporal non-local (MFTN) sub-nets. The SPAQ sub-net first models the spatial quality degradation based on spherical perception mechanism of human. Then, by exploiting motion cues across adjacent frames, the MPAQ sub-net properly incorporates motion contextual information for quality assessment on 360{\textdegree} video. Finally, the MFTN sub-net aggregates multi-frame quality degradation to yield the final quality score, via exploring long-term quality correlation from multiple frames. The experiments validate that our approach significantly advances the state-of-the-art BVQA performance on 360{\textdegree} video over two datasets, the code of which has been public in \url{https://github.com/yanglixiaoshen/ProVQA.}

Von Mises-Fisher Elliptical Distribution

A large class of modern probabilistic learning systems assumes symmetric distributions, however, real-world data tend to obey skewed distributions and are thus not always adequately modelled through symmetric distributions. To address this issue, elliptical distributions are increasingly used to generalise symmetric distributions, and further improvements to skewed elliptical distributions have recently attracted much attention. However, existing approaches are either hard to estimate or have complicated and abstract representations. To this end, we propose to employ the von-Mises-Fisher (vMF) distribution to obtain an explicit and simple probability representation of the skewed elliptical distribution. This is shown not only to allow us to deal with non-symmetric learning systems, but also to provide a physically meaningful way of generalising skewed distributions. For rigour, our extension is proved to share important and desirable properties with its symmetric counterpart. We also demonstrate that the proposed vMF distribution is both easy to generate and stable to estimate, both theoretically and through examples.

Meta-learning for Multi-variable Non-convex Optimization Problems: Iterating Non-optimums Makes Optimum Possible

In this paper, we aim to address the problem of solving a non-convex optimization problem over an intersection of multiple variable sets. This kind of problems is typically solved by using an alternating minimization (AM) strategy which splits the overall problem into a set of sub-problems corresponding to each variable, and then iteratively performs minimization over each sub-problem using a fixed updating rule. However, due to the intrinsic non-convexity of the overall problem, the optimization can usually be trapped into bad local minimum even when each sub-problem can be globally optimized at each iteration. To tackle this problem, we propose a meta-learning based Global Scope Optimization (GSO) method. It adaptively generates optimizers for sub-problems via meta-learners and constantly updates these meta-learners with respect to the global loss information of the overall problem. Therefore, the sub-problems are optimized with the objective of minimizing the global loss specifically. We evaluate the proposed model on a number of simulations, including solving bi-linear inverse problems: matrix completion, and non-linear problems: Gaussian mixture models. The experimental results show that our proposed approach outperforms AM-based methods in standard settings, and is able to achieve effective optimization in some challenging cases while other methods would typically fail.

Reciprocal Adversarial Learning via Characteristic Functions

Generative adversarial nets (GANs) have become a preferred tool for accommodating complicated distributions, and to stabilise the training and reduce the mode collapse of GANs, one of their main variants employs the integral probability metric (IPM) as the loss function. Although theoretically supported, extensive IPM-GANs are basically comparing moments in an embedded domain of the \textit{critic}. We generalise this by comparing the distributions rather than the moments via a powerful tool, i.e., the characteristic function (CF), which uniquely and universally contains all the information about a distribution. For rigour, we first establish the physical meaning of the phase and amplitude in CFs. This provides a feasible way of manipulating the generation. We then develop an efficient sampling way to calculate the CFs. Within this framework, we further prove an equivalence between the embedded and data domains when a reciprocal exists, which allows us to develop the GAN in an auto-encoder way, by using only two modules to achieve bi-directionally generating clear images. We refer to this efficient structure as the reciprocal CF GAN (RCF-GAN). Experimental results show the superior performances of the proposed RCF-GAN in terms of both generation and reconstruction.