Multi-task SAR Image Processing via GAN-based Unsupervised Manipulation

Generative Adversarial Networks (GANs) have shown tremendous potential in synthesizing a large number of realistic SAR images by learning patterns in the data distribution. Some GANs can achieve image editing by introducing latent codes, demonstrating significant promise in SAR image processing. Compared to traditional SAR image processing methods, editing based on GAN latent space control is entirely unsupervised, allowing image processing to be conducted without any labeled data. Additionally, the information extracted from the data is more interpretable. This paper proposes a novel SAR image processing framework called GAN-based Unsupervised Editing (GUE), aiming to address the following two issues: (1) disentangling semantic directions in the GAN latent space and finding meaningful directions; (2) establishing a comprehensive SAR image processing framework while achieving multiple image processing functions. In the implementation of GUE, we decompose the entangled semantic directions in the GAN latent space by training a carefully designed network. Moreover, we can accomplish multiple SAR image processing tasks (including despeckling, localization, auxiliary identification, and rotation editing) in a single training process without any form of supervision. Extensive experiments validate the effectiveness of the proposed method.

Graph Fourier Transform Enhancement through Envelope Extensions

Many real-world networks are characterized by directionality; however, the absence of an appropriate Fourier basis hinders the effective implementation of graph signal processing techniques. Inspired by discrete signal processing, where embedding a line digraph into a cycle digraph facilitates the powerful Discrete Fourier Transform for signal analysis, addressing the structural complexities of general digraphs can help overcome the limitations of the Graph Fourier Transform (GFT) and unlock its potential. The Discrete Fourier Transform (DFT) serves as a Graph Fourier Transform for both cycle graphs and Cayley digraphs on the finite cyclic groups $\mathbb{Z}_N$. We propose a systematic method to identify a class of such Cayley digraphs that can encompass a given directed graph. By embedding the directed graph into these Cayley digraphs and opting for envelope extensions that naturally support the Graph Fourier Transform, the GFT functionalities of these extensions can be harnessed for signal analysis. Among the potential envelopes, optimal performance is achieved by selecting one that meets key properties. This envelope's structure closely aligns with the characteristics of the original digraph. The Graph Fourier Transform of this envelope is reliable in terms of numerical stability, and its columns approximately form an eigenbasis for the adjacency matrix associated with the original digraph. It is shown that the envelope extensions possess a convolution product, with their GFT fulfilling the convolution theorem. Additionally, shift-invariant graph filters (systems) are described as the convolution operator, analogous to the classical case. This allows the utilization of systems for signal analysis.

Fourier Analysis of Signals on Directed Acyclic Graphs (DAG) Using Graph Zero-Padding

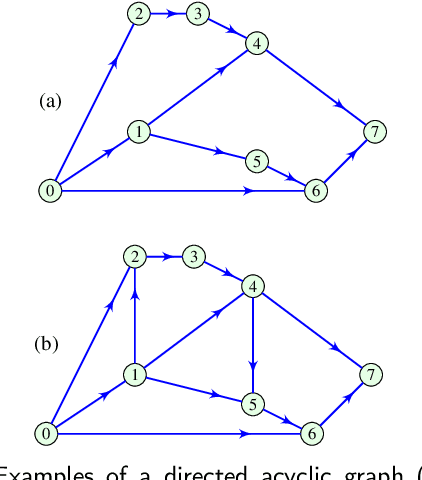
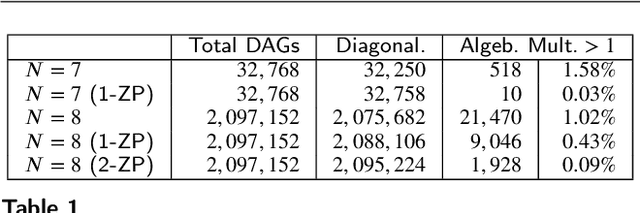
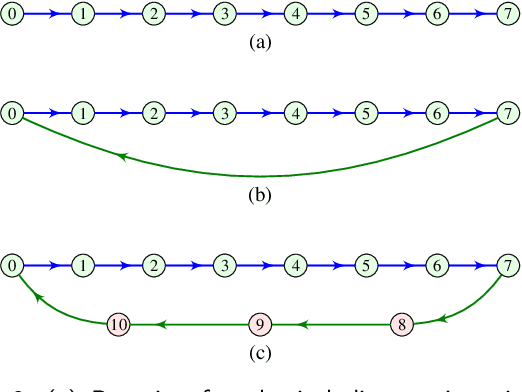
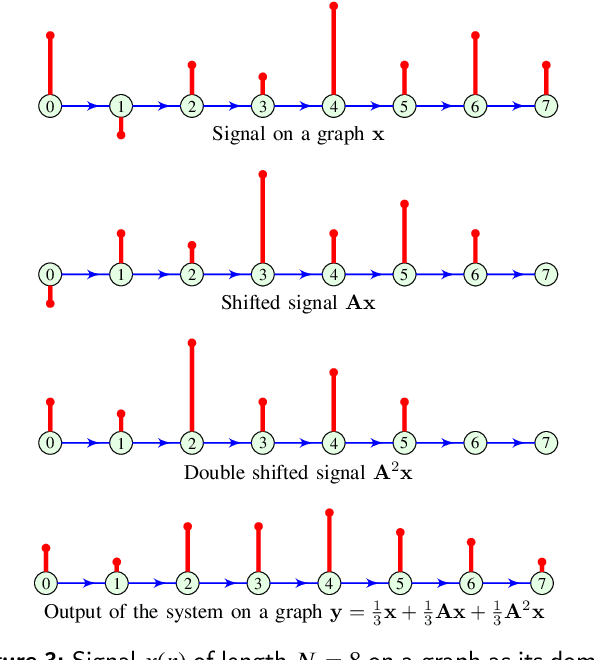
Directed acyclic graphs (DAGs) are used for modeling causal relationships, dependencies, and flows in various systems. However, spectral analysis becomes impractical in this setting because the eigen-decomposition of the adjacency matrix yields all eigenvalues equal to zero. This inherent property of DAGs results in an inability to differentiate between frequency components of signals on such graphs. This problem can be addressed by alternating the Fourier basis or adding edges in a DAG. However, these approaches change the physics of the considered problem. To address this limitation, we propose a graph zero-padding approach. This approach involves augmenting the original DAG with additional vertices that are connected to the existing structure. The added vertices are characterized by signal values set to zero. The proposed technique enables the spectral evaluation of system outputs on DAGs (in almost all cases), that is the computation of vertex-domain convolution without the adverse effects of aliasing due to changes in a graph structure, with the ultimate goal of preserving the output of the system on a graph as if the changes in the graph structure were not done.

Eigenvalues of Symmetric Non-normalized Discrete Trigonometric Transforms

A comprehensive approach to the spectrum characterization (derivation of eigenvalues and the corresponding multiplicities) for non-normalized, symmetric discrete trigonometric transforms (DTT) is presented in the paper. Eight types of the DTT are analyzed. New explicit analytic expressions for the eigenvalues, together with their multiplicities, for the cases of three DTT (DCT$_{(1)}$, DCT$_{(5)}$, and DST$_{(8)}$), are the main contribution of this paper. Moreover, the presented theory is supplemented by new, original derivations for the closed-form expressions of the square and the trace of analyzed DTT matrices.

Cluster-CAM: Cluster-Weighted Visual Interpretation of CNNs' Decision in Image Classification

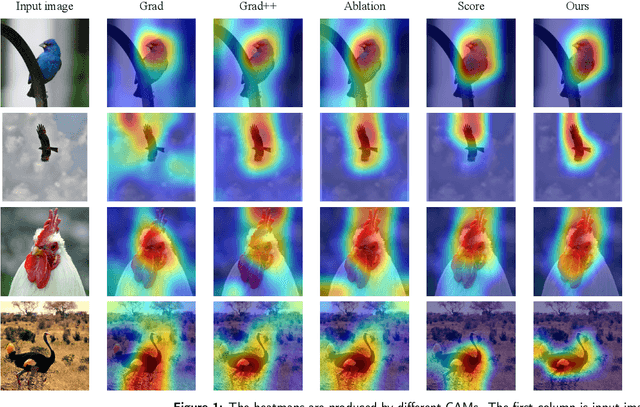
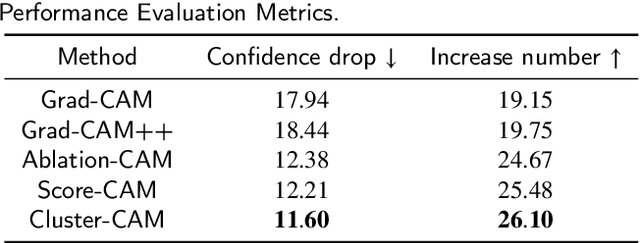
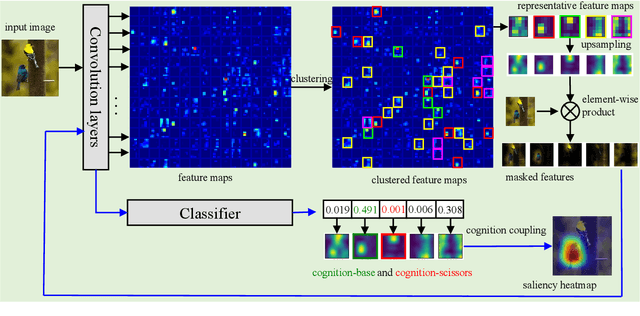
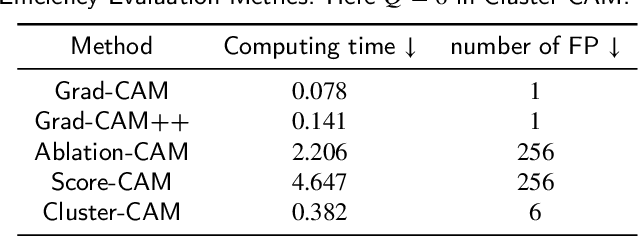
Despite the tremendous success of convolutional neural networks (CNNs) in computer vision, the mechanism of CNNs still lacks clear interpretation. Currently, class activation mapping (CAM), a famous visualization technique to interpret CNN's decision, has drawn increasing attention. Gradient-based CAMs are efficient while the performance is heavily affected by gradient vanishing and exploding. In contrast, gradient-free CAMs can avoid computing gradients to produce more understandable results. However, existing gradient-free CAMs are quite time-consuming because hundreds of forward interference per image are required. In this paper, we proposed Cluster-CAM, an effective and efficient gradient-free CNN interpretation algorithm. Cluster-CAM can significantly reduce the times of forward propagation by splitting the feature maps into clusters in an unsupervised manner. Furthermore, we propose an artful strategy to forge a cognition-base map and cognition-scissors from clustered feature maps. The final salience heatmap will be computed by merging the above cognition maps. Qualitative results conspicuously show that Cluster-CAM can produce heatmaps where the highlighted regions match the human's cognition more precisely than existing CAMs. The quantitative evaluation further demonstrates the superiority of Cluster-CAM in both effectiveness and efficiency.

Fair and skill-diverse student group formation via constrained k-way graph partitioning

Forming the right combination of students in a group promises to enable a powerful and effective environment for learning and collaboration. However, defining a group of students is a complex task which has to satisfy multiple constraints. This work introduces an unsupervised algorithm for fair and skill-diverse student group formation. This is achieved by taking account of student course marks and sensitive attributes provided by the education office. The skill sets of students are determined using unsupervised dimensionality reduction of course mark data via the Laplacian eigenmap. The problem is formulated as a constrained graph partitioning problem, whereby the diversity of skill sets in each group are maximised, group sizes are upper and lower bounded according to available resources, and `balance' of a sensitive attribute is lower bounded to enforce fairness in group formation. This optimisation problem is solved using integer programming and its effectiveness is demonstrated on a dataset of student course marks from Imperial College London.

Demystifying CNNs for Images by Matched Filters

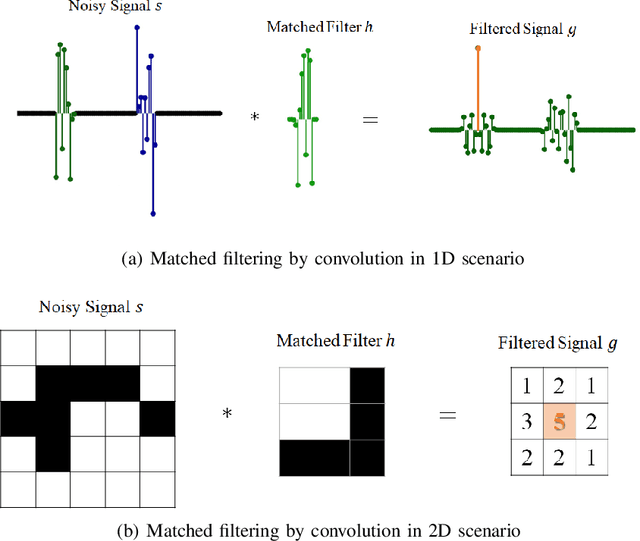
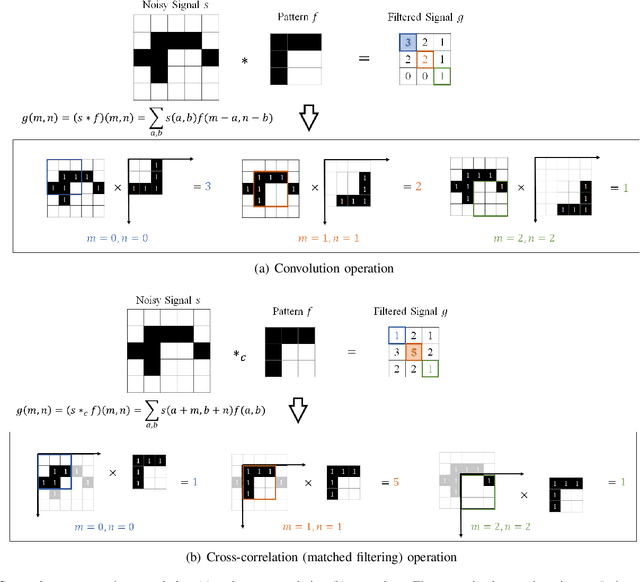
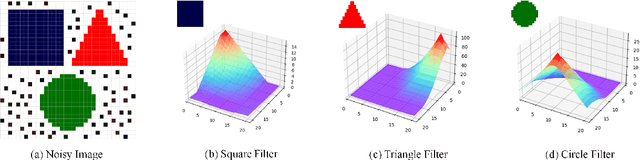
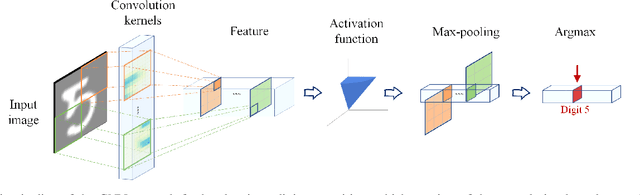
The success of convolution neural networks (CNN) has been revolutionising the way we approach and use intelligent machines in the Big Data era. Despite success, CNNs have been consistently put under scrutiny owing to their \textit{black-box} nature, an \textit{ad hoc} manner of their construction, together with the lack of theoretical support and physical meanings of their operation. This has been prohibitive to both the quantitative and qualitative understanding of CNNs, and their application in more sensitive areas such as AI for health. We set out to address these issues, and in this way demystify the operation of CNNs, by employing the perspective of matched filtering. We first illuminate that the convolution operation, the very core of CNNs, represents a matched filter which aims to identify the presence of features in input data. This then serves as a vehicle to interpret the convolution-activation-pooling chain in CNNs under the theoretical umbrella of matched filtering, a common operation in signal processing. We further provide extensive examples and experiments to illustrate this connection, whereby the learning in CNNs is shown to also perform matched filtering, which further sheds light onto physical meaning of learnt parameters and layers. It is our hope that this material will provide new insights into the understanding, constructing and analysing of CNNs, as well as paving the way for developing new methods and architectures of CNNs.

VS-CAM: Vertex Semantic Class Activation Mapping to Interpret Vision Graph Neural Network

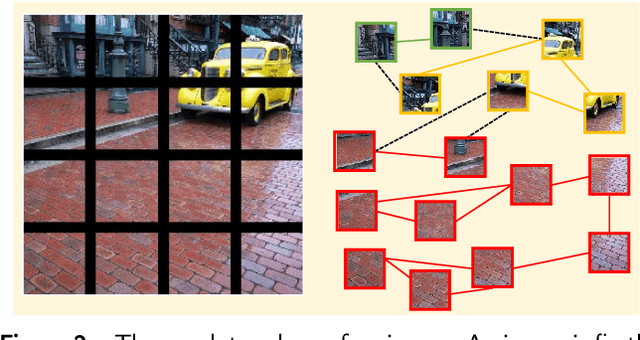
Graph convolutional neural network (GCN) has drawn increasing attention and attained good performance in various computer vision tasks, however, there lacks a clear interpretation of GCN's inner mechanism. For standard convolutional neural networks (CNNs), class activation mapping (CAM) methods are commonly used to visualize the connection between CNN's decision and image region by generating a heatmap. Nonetheless, such heatmap usually exhibits semantic-chaos when these CAMs are applied to GCN directly. In this paper, we proposed a novel visualization method particularly applicable to GCN, Vertex Semantic Class Activation Mapping (VS-CAM). VS-CAM includes two independent pipelines to produce a set of semantic-probe maps and a semantic-base map, respectively. Semantic-probe maps are used to detect the semantic information from semantic-base map to aggregate a semantic-aware heatmap. Qualitative results show that VS-CAM can obtain heatmaps where the highlighted regions match the objects much more precisely than CNN-based CAM. The quantitative evaluation further demonstrates the superiority of VS-CAM.

Analytical Interpretation of Latent Codes in InfoGAN with SAR Images

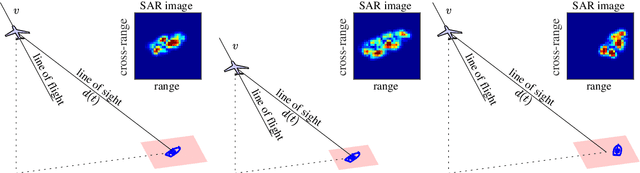
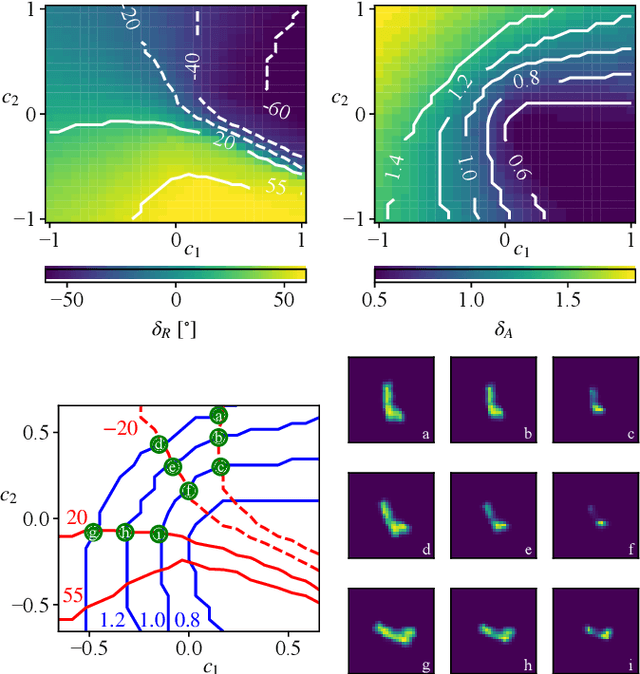
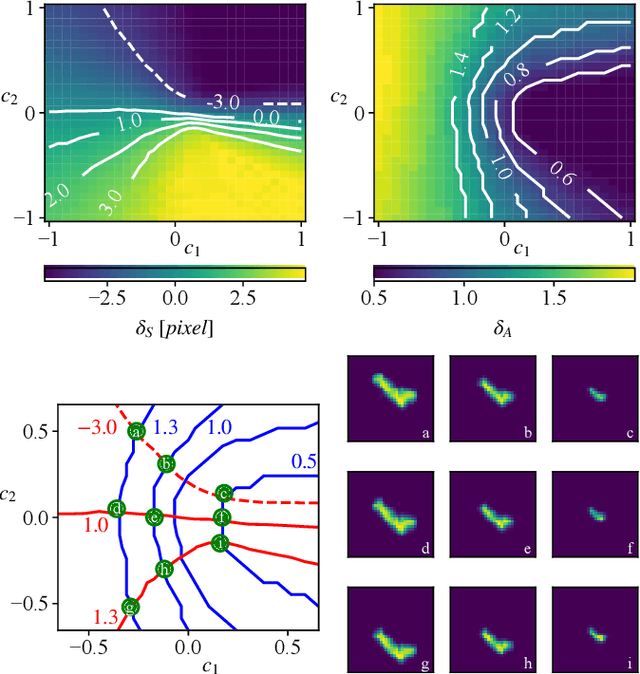
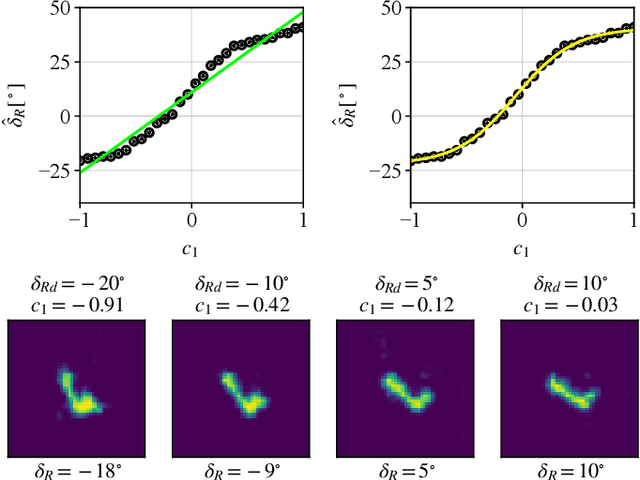
Generative Adversarial Networks (GANs) can synthesize abundant photo-realistic synthetic aperture radar (SAR) images. Some recent GANs (e.g., InfoGAN), are even able to edit specific properties of the synthesized images by introducing latent codes. It is crucial for SAR image synthesis since the targets in real SAR images are with different properties due to the imaging mechanism. Despite the success of InfoGAN in manipulating properties, there still lacks a clear explanation of how these latent codes affect synthesized properties, thus editing specific properties usually relies on empirical trials, unreliable and time-consuming. In this paper, we show that latent codes are disentangled to affect the properties of SAR images in a non-linear manner. By introducing some property estimators for latent codes, we are able to provide a completely analytical nonlinear model to decompose the entangled causality between latent codes and different properties. The qualitative and quantitative experimental results further reveal that the properties can be calculated by latent codes, inversely, the satisfying latent codes can be estimated given desired properties. In this case, properties can be manipulated by latent codes as we expect.

Convolutional Neural Networks Demystified: A Matched Filtering Perspective Based Tutorial

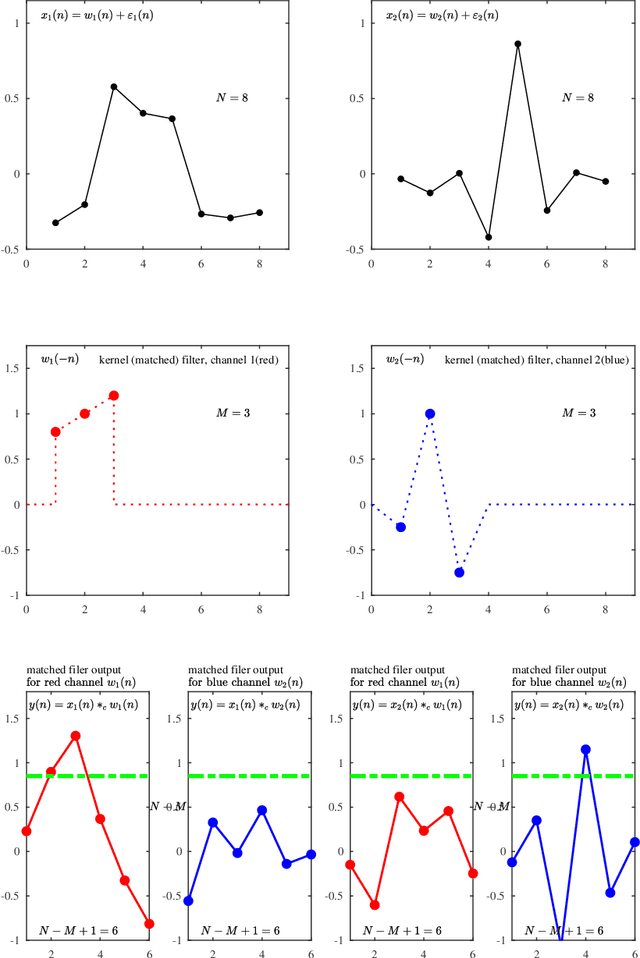
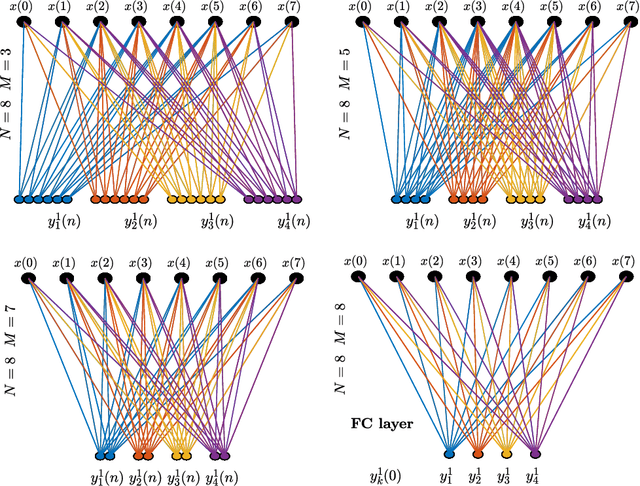
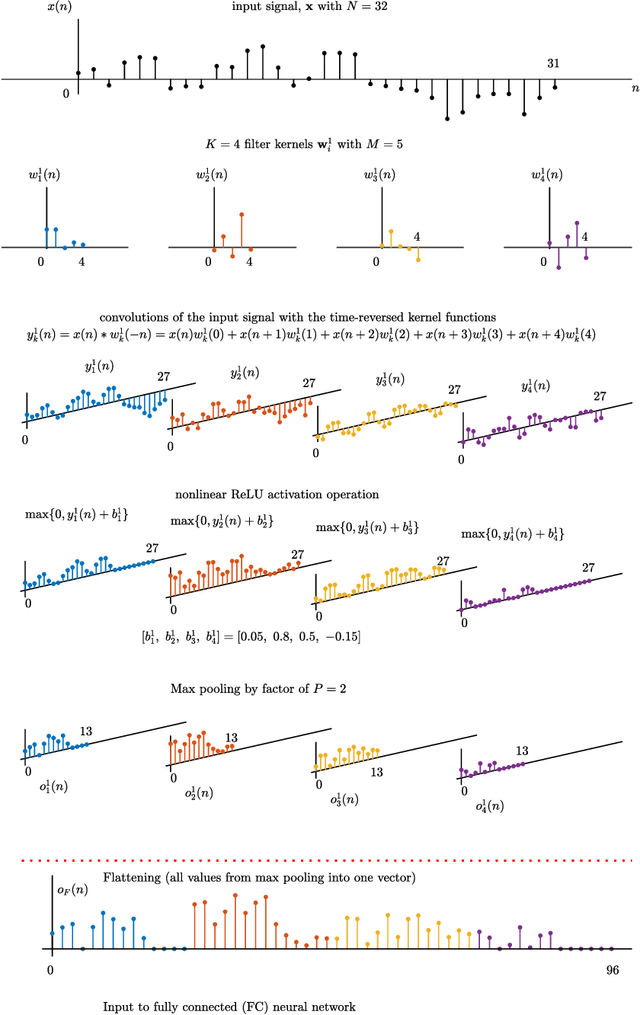
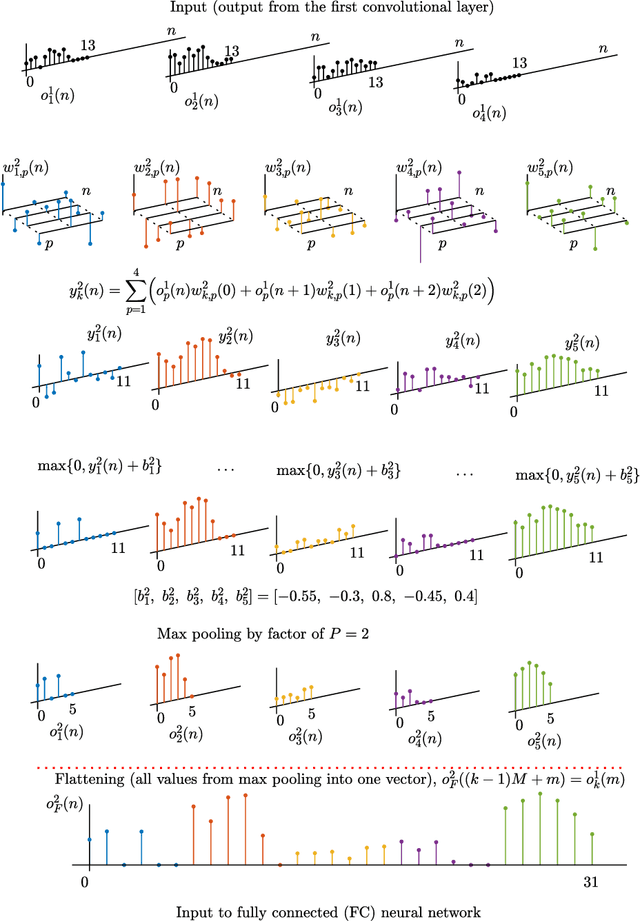
Deep Neural Networks (DNN) and especially Convolutional Neural Networks (CNN) are a de-facto standard for the analysis of large volumes of signals and images. Yet, their development and underlying principles have been largely performed in an ad-hoc and black box fashion. To help demystify CNNs, we revisit their operation from first principles and a matched filtering perspective. We establish that the convolution operation within CNNs, their very backbone, represents a matched filter which examines the input signal/image for the presence of pre-defined features. This perspective is shown to be physically meaningful, and serves as a basis for a step-by-step tutorial on the operation of CNNs, including pooling, zero padding, various ways of dimensionality reduction. Starting from first principles, both the feed-forward pass and the learning stage (via back-propagation) are illuminated in detail, both through a worked-out numerical example and the corresponding visualizations. It is our hope that this tutorial will help shed new light and physical intuition into the understanding and further development of deep neural networks.