Fourier Analysis of Signals on Directed Acyclic Graphs (DAG) Using Graph Zero-Padding

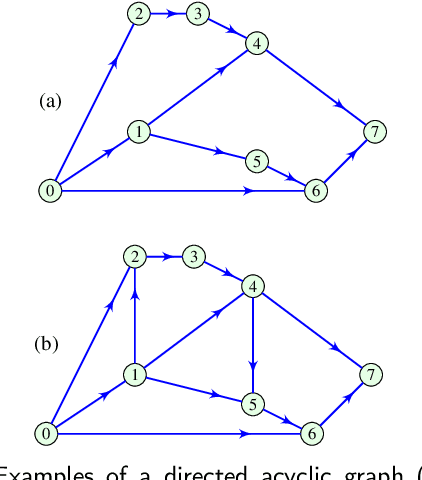
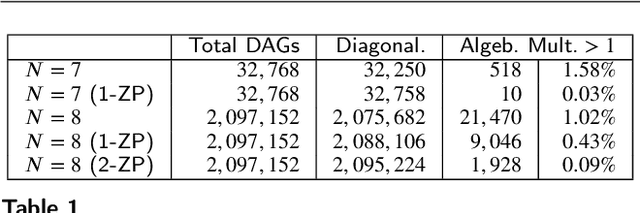
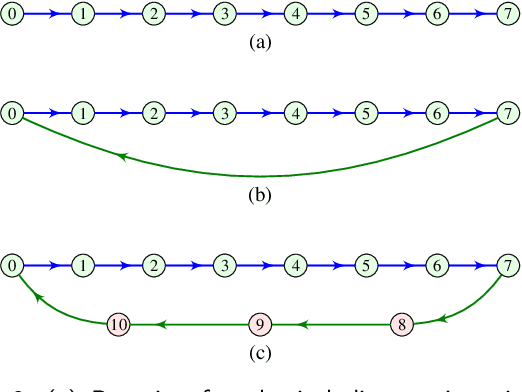
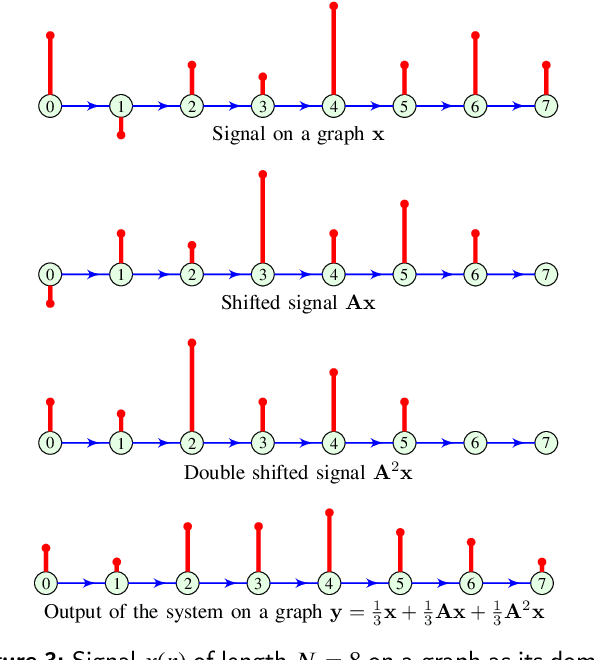
Directed acyclic graphs (DAGs) are used for modeling causal relationships, dependencies, and flows in various systems. However, spectral analysis becomes impractical in this setting because the eigen-decomposition of the adjacency matrix yields all eigenvalues equal to zero. This inherent property of DAGs results in an inability to differentiate between frequency components of signals on such graphs. This problem can be addressed by alternating the Fourier basis or adding edges in a DAG. However, these approaches change the physics of the considered problem. To address this limitation, we propose a graph zero-padding approach. This approach involves augmenting the original DAG with additional vertices that are connected to the existing structure. The added vertices are characterized by signal values set to zero. The proposed technique enables the spectral evaluation of system outputs on DAGs (in almost all cases), that is the computation of vertex-domain convolution without the adverse effects of aliasing due to changes in a graph structure, with the ultimate goal of preserving the output of the system on a graph as if the changes in the graph structure were not done.

Improved Coherence Index-Based Bound in Compressive Sensing

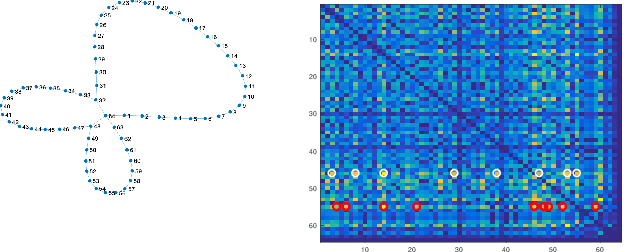
Within the Compressive Sensing (CS) paradigm, sparse signals can be reconstructed based on a reduced set of measurements. Reliability of the solution is determined by the uniqueness condition. With its mathematically tractable and feasible calculation, coherence index is one of very few CS metrics with a considerable practical importance. In this paper, we propose an improvement of the coherence based uniqueness relation for the matching pursuit algorithms. Starting from a simple and intuitive derivation of the standard uniqueness condition based on the coherence index, we derive a less conservative coherence index-based lower bound for signal sparsity. The results are generalized to the uniqueness condition of the $l_0$-norm minimization for a signal represented in two orthonormal bases.

Graph Signal Processing -- Part III: Machine Learning on Graphs, from Graph Topology to Applications

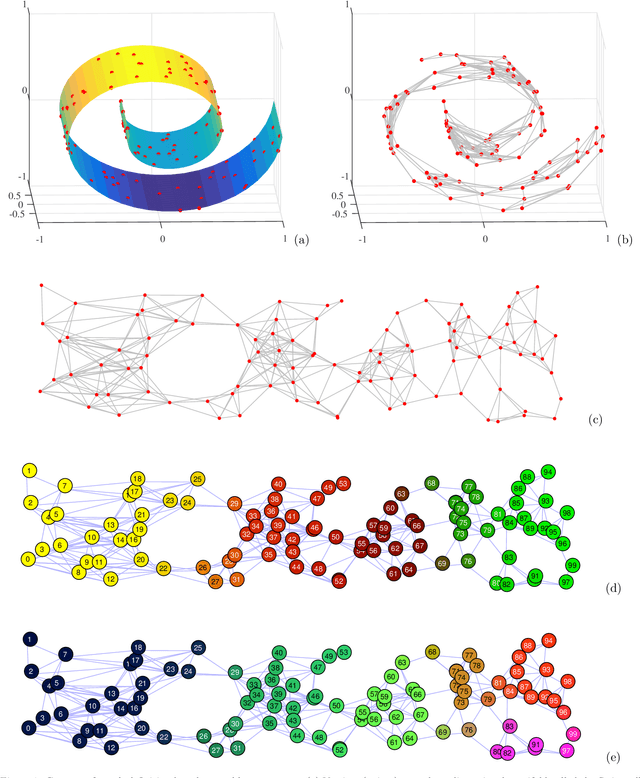
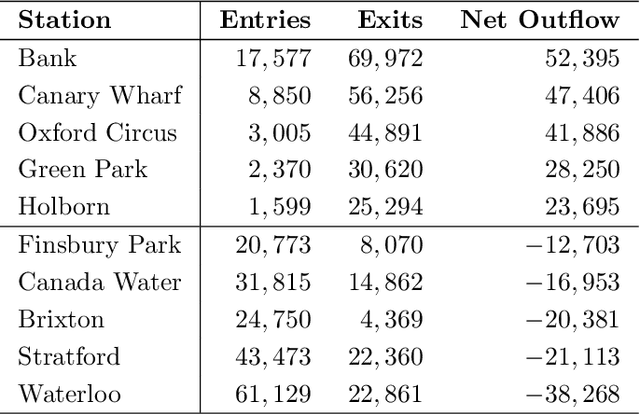
Many modern data analytics applications on graphs operate on domains where graph topology is not known a priori, and hence its determination becomes part of the problem definition, rather than serving as prior knowledge which aids the problem solution. Part III of this monograph starts by addressing ways to learn graph topology, from the case where the physics of the problem already suggest a possible topology, through to most general cases where the graph topology is learned from the data. A particular emphasis is on graph topology definition based on the correlation and precision matrices of the observed data, combined with additional prior knowledge and structural conditions, such as the smoothness or sparsity of graph connections. For learning sparse graphs (with small number of edges), the least absolute shrinkage and selection operator, known as LASSO is employed, along with its graph specific variant, graphical LASSO. For completeness, both variants of LASSO are derived in an intuitive way, and explained. An in-depth elaboration of the graph topology learning paradigm is provided through several examples on physically well defined graphs, such as electric circuits, linear heat transfer, social and computer networks, and spring-mass systems. As many graph neural networks (GNN) and convolutional graph networks (GCN) are emerging, we have also reviewed the main trends in GNNs and GCNs, from the perspective of graph signal filtering. Tensor representation of lattice-structured graphs is next considered, and it is shown that tensors (multidimensional data arrays) are a special class of graph signals, whereby the graph vertices reside on a high-dimensional regular lattice structure. This part of monograph concludes with two emerging applications in financial data processing and underground transportation networks modeling.

Detection of irregular QRS complexes using Hermite Transform and Support Vector Machine

Computer based recognition and detection of abnormalities in ECG signals is proposed. For this purpose, the Support Vector Machines (SVM) are combined with the advantages of Hermite transform representation. SVM represent a special type of classification techniques commonly used in medical applications. Automatic classification of ECG could make the work of cardiologic departments faster and more efficient. It would also reduce the number of false diagnosis and, as a result, save lives. The working principle of the SVM is based on translating the data into a high dimensional feature space and separating it using a linear classificator. In order to provide an optimal representation for SVM application, the Hermite transform domain is used. This domain is proved to be suitable because of the similarity of the QRS complex with Hermite basis functions. The maximal signal information is obtained using a small set of features that are used for detection of irregular QRS complexes. The aim of the paper is to show that these features can be employed for automatic ECG signal analysis.