Graph Fourier Transform Enhancement through Envelope Extensions

Many real-world networks are characterized by directionality; however, the absence of an appropriate Fourier basis hinders the effective implementation of graph signal processing techniques. Inspired by discrete signal processing, where embedding a line digraph into a cycle digraph facilitates the powerful Discrete Fourier Transform for signal analysis, addressing the structural complexities of general digraphs can help overcome the limitations of the Graph Fourier Transform (GFT) and unlock its potential. The Discrete Fourier Transform (DFT) serves as a Graph Fourier Transform for both cycle graphs and Cayley digraphs on the finite cyclic groups $\mathbb{Z}_N$. We propose a systematic method to identify a class of such Cayley digraphs that can encompass a given directed graph. By embedding the directed graph into these Cayley digraphs and opting for envelope extensions that naturally support the Graph Fourier Transform, the GFT functionalities of these extensions can be harnessed for signal analysis. Among the potential envelopes, optimal performance is achieved by selecting one that meets key properties. This envelope's structure closely aligns with the characteristics of the original digraph. The Graph Fourier Transform of this envelope is reliable in terms of numerical stability, and its columns approximately form an eigenbasis for the adjacency matrix associated with the original digraph. It is shown that the envelope extensions possess a convolution product, with their GFT fulfilling the convolution theorem. Additionally, shift-invariant graph filters (systems) are described as the convolution operator, analogous to the classical case. This allows the utilization of systems for signal analysis.

Fourier Analysis of Signals on Directed Acyclic Graphs (DAG) Using Graph Zero-Padding

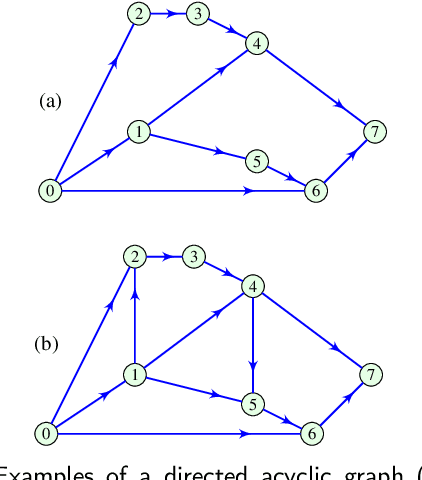
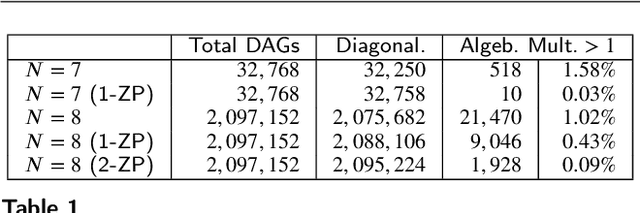
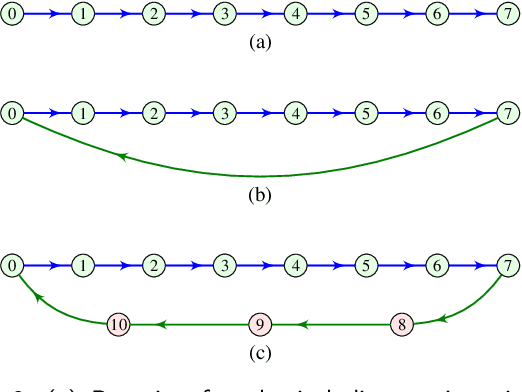
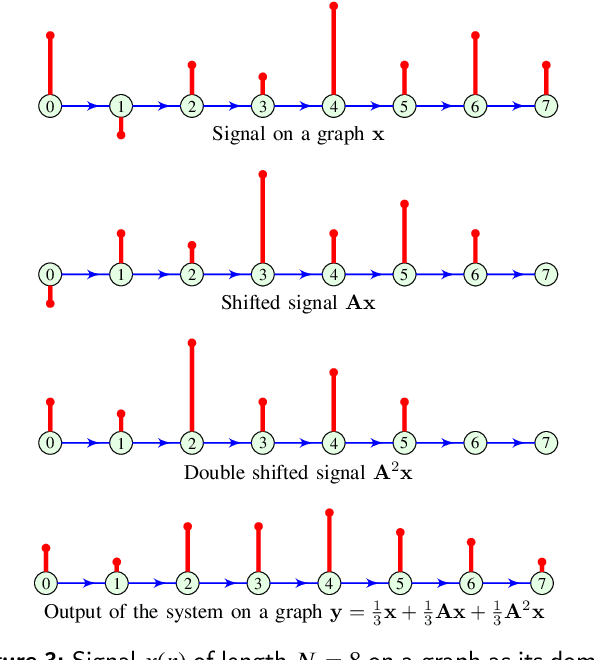
Directed acyclic graphs (DAGs) are used for modeling causal relationships, dependencies, and flows in various systems. However, spectral analysis becomes impractical in this setting because the eigen-decomposition of the adjacency matrix yields all eigenvalues equal to zero. This inherent property of DAGs results in an inability to differentiate between frequency components of signals on such graphs. This problem can be addressed by alternating the Fourier basis or adding edges in a DAG. However, these approaches change the physics of the considered problem. To address this limitation, we propose a graph zero-padding approach. This approach involves augmenting the original DAG with additional vertices that are connected to the existing structure. The added vertices are characterized by signal values set to zero. The proposed technique enables the spectral evaluation of system outputs on DAGs (in almost all cases), that is the computation of vertex-domain convolution without the adverse effects of aliasing due to changes in a graph structure, with the ultimate goal of preserving the output of the system on a graph as if the changes in the graph structure were not done.

Eigenvalues of Symmetric Non-normalized Discrete Trigonometric Transforms

A comprehensive approach to the spectrum characterization (derivation of eigenvalues and the corresponding multiplicities) for non-normalized, symmetric discrete trigonometric transforms (DTT) is presented in the paper. Eight types of the DTT are analyzed. New explicit analytic expressions for the eigenvalues, together with their multiplicities, for the cases of three DTT (DCT$_{(1)}$, DCT$_{(5)}$, and DST$_{(8)}$), are the main contribution of this paper. Moreover, the presented theory is supplemented by new, original derivations for the closed-form expressions of the square and the trace of analyzed DTT matrices.

Cluster-CAM: Cluster-Weighted Visual Interpretation of CNNs' Decision in Image Classification

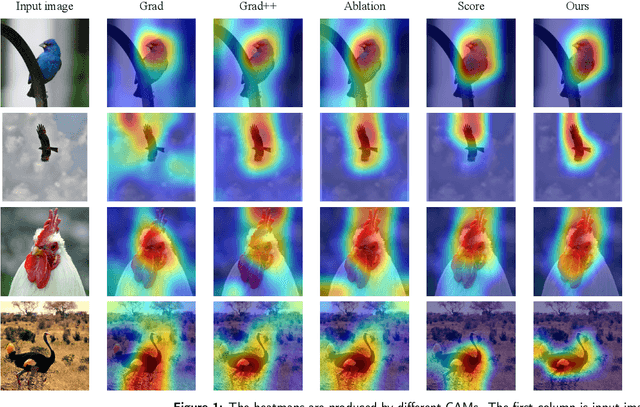
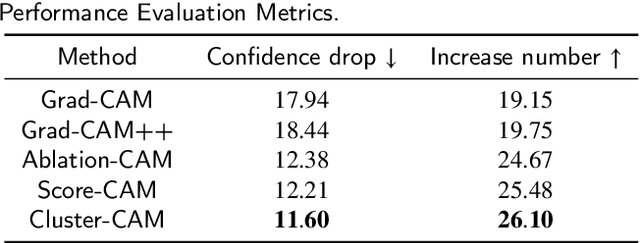
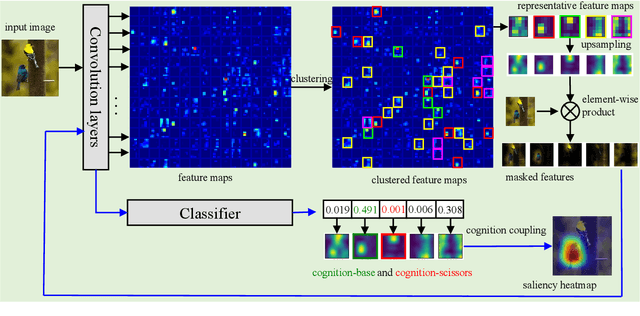
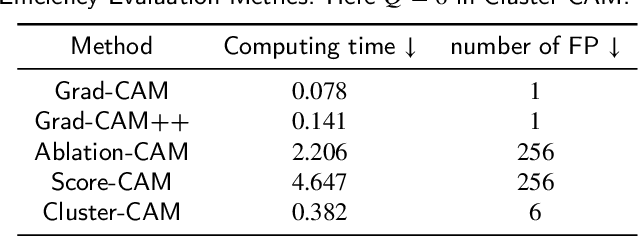
Despite the tremendous success of convolutional neural networks (CNNs) in computer vision, the mechanism of CNNs still lacks clear interpretation. Currently, class activation mapping (CAM), a famous visualization technique to interpret CNN's decision, has drawn increasing attention. Gradient-based CAMs are efficient while the performance is heavily affected by gradient vanishing and exploding. In contrast, gradient-free CAMs can avoid computing gradients to produce more understandable results. However, existing gradient-free CAMs are quite time-consuming because hundreds of forward interference per image are required. In this paper, we proposed Cluster-CAM, an effective and efficient gradient-free CNN interpretation algorithm. Cluster-CAM can significantly reduce the times of forward propagation by splitting the feature maps into clusters in an unsupervised manner. Furthermore, we propose an artful strategy to forge a cognition-base map and cognition-scissors from clustered feature maps. The final salience heatmap will be computed by merging the above cognition maps. Qualitative results conspicuously show that Cluster-CAM can produce heatmaps where the highlighted regions match the human's cognition more precisely than existing CAMs. The quantitative evaluation further demonstrates the superiority of Cluster-CAM in both effectiveness and efficiency.

Analytical Interpretation of Latent Codes in InfoGAN with SAR Images

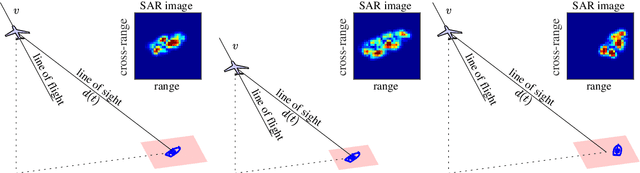
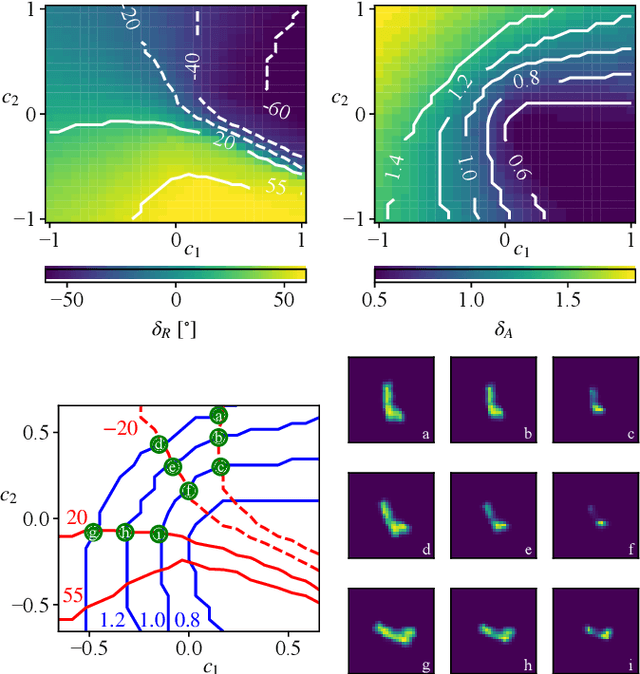
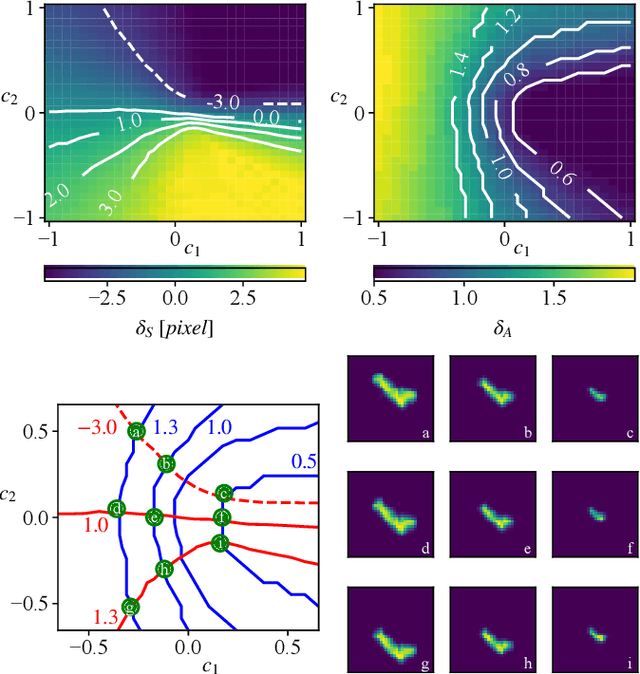
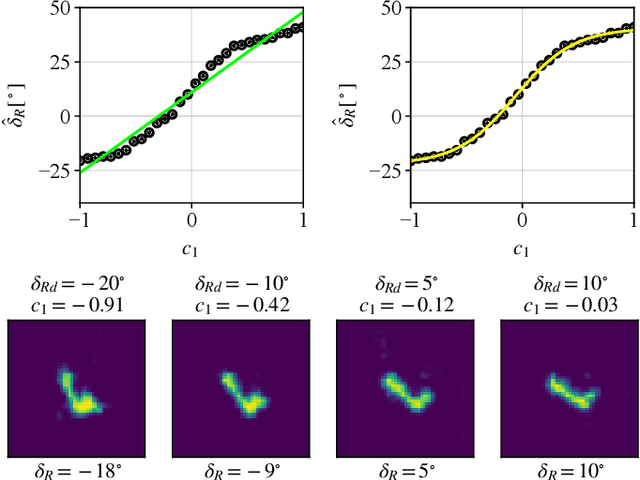
Generative Adversarial Networks (GANs) can synthesize abundant photo-realistic synthetic aperture radar (SAR) images. Some recent GANs (e.g., InfoGAN), are even able to edit specific properties of the synthesized images by introducing latent codes. It is crucial for SAR image synthesis since the targets in real SAR images are with different properties due to the imaging mechanism. Despite the success of InfoGAN in manipulating properties, there still lacks a clear explanation of how these latent codes affect synthesized properties, thus editing specific properties usually relies on empirical trials, unreliable and time-consuming. In this paper, we show that latent codes are disentangled to affect the properties of SAR images in a non-linear manner. By introducing some property estimators for latent codes, we are able to provide a completely analytical nonlinear model to decompose the entangled causality between latent codes and different properties. The qualitative and quantitative experimental results further reveal that the properties can be calculated by latent codes, inversely, the satisfying latent codes can be estimated given desired properties. In this case, properties can be manipulated by latent codes as we expect.

Improved Coherence Index-Based Bound in Compressive Sensing

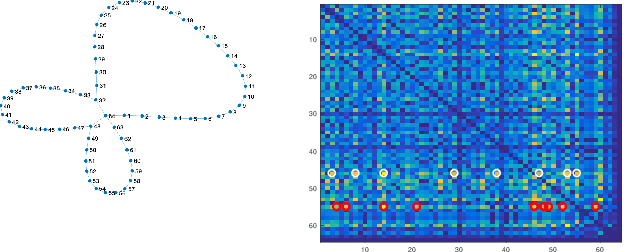
Within the Compressive Sensing (CS) paradigm, sparse signals can be reconstructed based on a reduced set of measurements. Reliability of the solution is determined by the uniqueness condition. With its mathematically tractable and feasible calculation, coherence index is one of very few CS metrics with a considerable practical importance. In this paper, we propose an improvement of the coherence based uniqueness relation for the matching pursuit algorithms. Starting from a simple and intuitive derivation of the standard uniqueness condition based on the coherence index, we derive a less conservative coherence index-based lower bound for signal sparsity. The results are generalized to the uniqueness condition of the $l_0$-norm minimization for a signal represented in two orthonormal bases.

Graph Signal Processing -- Part III: Machine Learning on Graphs, from Graph Topology to Applications

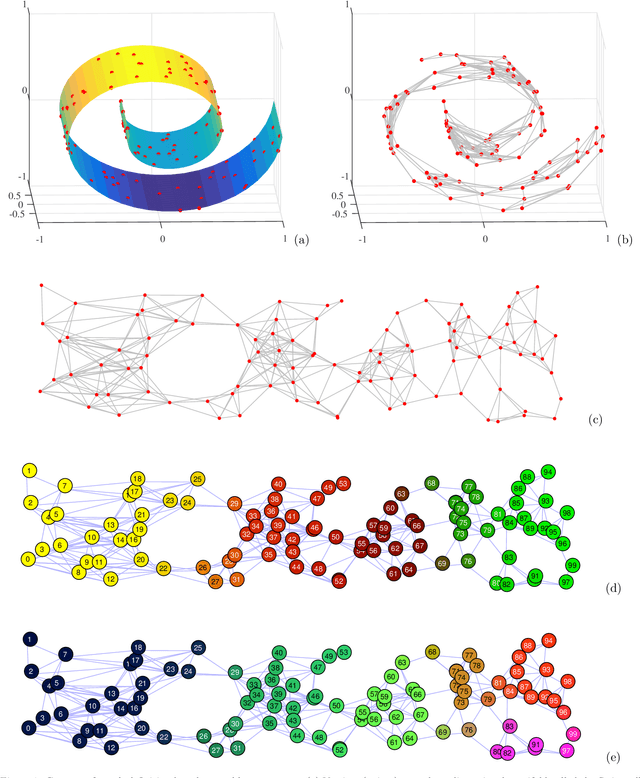
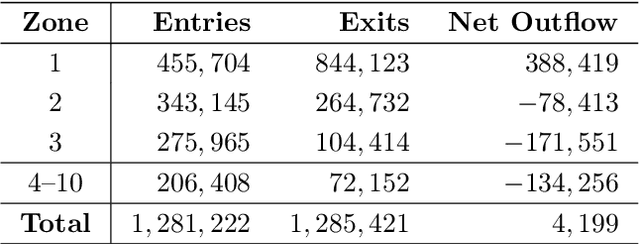
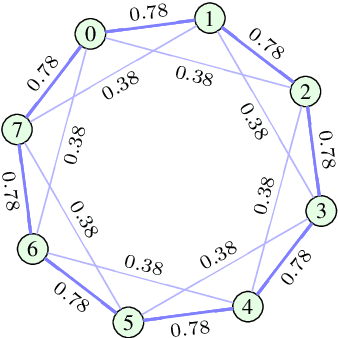
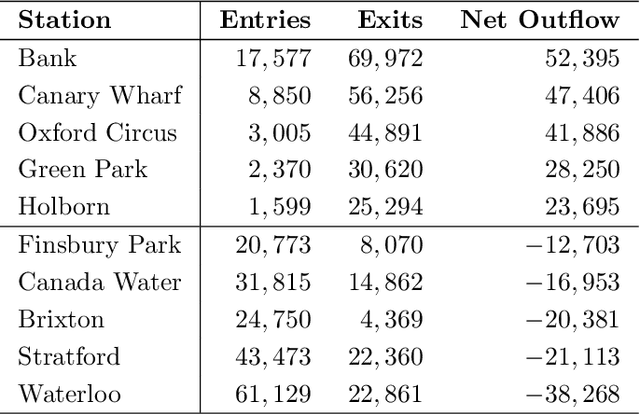
Many modern data analytics applications on graphs operate on domains where graph topology is not known a priori, and hence its determination becomes part of the problem definition, rather than serving as prior knowledge which aids the problem solution. Part III of this monograph starts by addressing ways to learn graph topology, from the case where the physics of the problem already suggest a possible topology, through to most general cases where the graph topology is learned from the data. A particular emphasis is on graph topology definition based on the correlation and precision matrices of the observed data, combined with additional prior knowledge and structural conditions, such as the smoothness or sparsity of graph connections. For learning sparse graphs (with small number of edges), the least absolute shrinkage and selection operator, known as LASSO is employed, along with its graph specific variant, graphical LASSO. For completeness, both variants of LASSO are derived in an intuitive way, and explained. An in-depth elaboration of the graph topology learning paradigm is provided through several examples on physically well defined graphs, such as electric circuits, linear heat transfer, social and computer networks, and spring-mass systems. As many graph neural networks (GNN) and convolutional graph networks (GCN) are emerging, we have also reviewed the main trends in GNNs and GCNs, from the perspective of graph signal filtering. Tensor representation of lattice-structured graphs is next considered, and it is shown that tensors (multidimensional data arrays) are a special class of graph signals, whereby the graph vertices reside on a high-dimensional regular lattice structure. This part of monograph concludes with two emerging applications in financial data processing and underground transportation networks modeling.