Graph Fourier Transform Enhancement through Envelope Extensions

Many real-world networks are characterized by directionality; however, the absence of an appropriate Fourier basis hinders the effective implementation of graph signal processing techniques. Inspired by discrete signal processing, where embedding a line digraph into a cycle digraph facilitates the powerful Discrete Fourier Transform for signal analysis, addressing the structural complexities of general digraphs can help overcome the limitations of the Graph Fourier Transform (GFT) and unlock its potential. The Discrete Fourier Transform (DFT) serves as a Graph Fourier Transform for both cycle graphs and Cayley digraphs on the finite cyclic groups $\mathbb{Z}_N$. We propose a systematic method to identify a class of such Cayley digraphs that can encompass a given directed graph. By embedding the directed graph into these Cayley digraphs and opting for envelope extensions that naturally support the Graph Fourier Transform, the GFT functionalities of these extensions can be harnessed for signal analysis. Among the potential envelopes, optimal performance is achieved by selecting one that meets key properties. This envelope's structure closely aligns with the characteristics of the original digraph. The Graph Fourier Transform of this envelope is reliable in terms of numerical stability, and its columns approximately form an eigenbasis for the adjacency matrix associated with the original digraph. It is shown that the envelope extensions possess a convolution product, with their GFT fulfilling the convolution theorem. Additionally, shift-invariant graph filters (systems) are described as the convolution operator, analogous to the classical case. This allows the utilization of systems for signal analysis.

Fourier Analysis of Signals on Directed Acyclic Graphs (DAG) Using Graph Zero-Padding

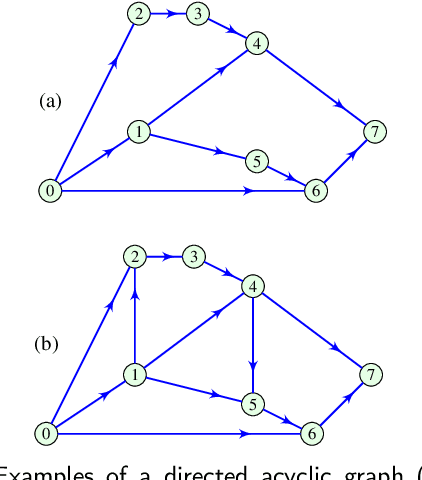
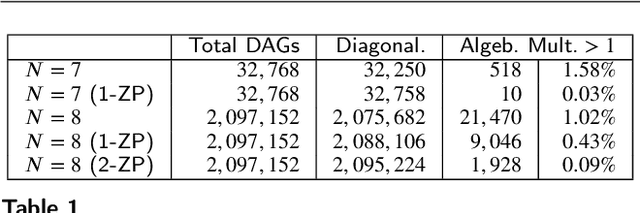
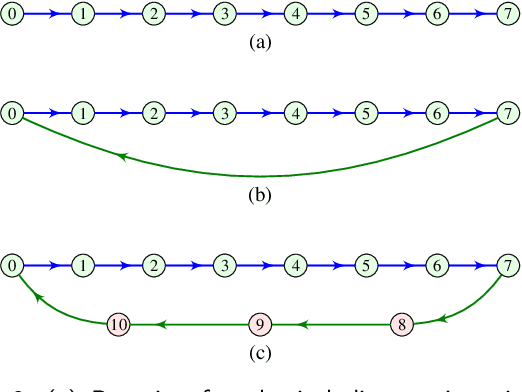
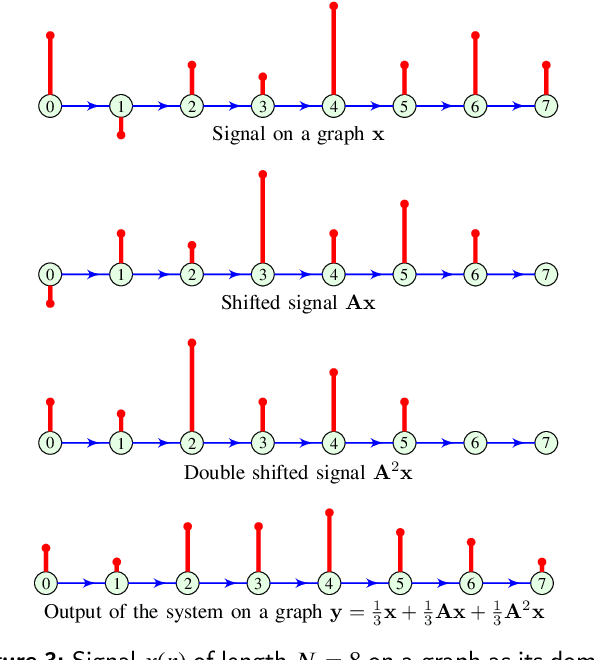
Directed acyclic graphs (DAGs) are used for modeling causal relationships, dependencies, and flows in various systems. However, spectral analysis becomes impractical in this setting because the eigen-decomposition of the adjacency matrix yields all eigenvalues equal to zero. This inherent property of DAGs results in an inability to differentiate between frequency components of signals on such graphs. This problem can be addressed by alternating the Fourier basis or adding edges in a DAG. However, these approaches change the physics of the considered problem. To address this limitation, we propose a graph zero-padding approach. This approach involves augmenting the original DAG with additional vertices that are connected to the existing structure. The added vertices are characterized by signal values set to zero. The proposed technique enables the spectral evaluation of system outputs on DAGs (in almost all cases), that is the computation of vertex-domain convolution without the adverse effects of aliasing due to changes in a graph structure, with the ultimate goal of preserving the output of the system on a graph as if the changes in the graph structure were not done.

Eigenvalues of Symmetric Non-normalized Discrete Trigonometric Transforms

A comprehensive approach to the spectrum characterization (derivation of eigenvalues and the corresponding multiplicities) for non-normalized, symmetric discrete trigonometric transforms (DTT) is presented in the paper. Eight types of the DTT are analyzed. New explicit analytic expressions for the eigenvalues, together with their multiplicities, for the cases of three DTT (DCT$_{(1)}$, DCT$_{(5)}$, and DST$_{(8)}$), are the main contribution of this paper. Moreover, the presented theory is supplemented by new, original derivations for the closed-form expressions of the square and the trace of analyzed DTT matrices.