Dynamic Portfolio Cuts: A Spectral Approach to Graph-Theoretic Diversification

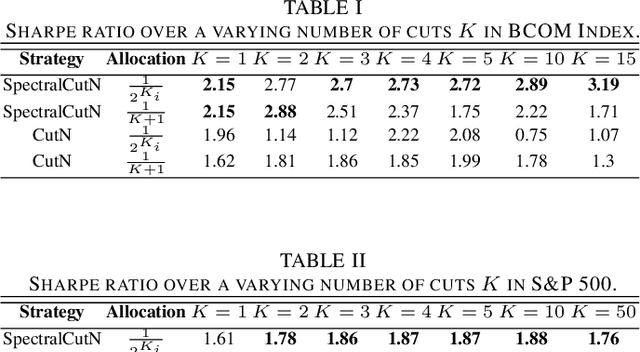
Stock market returns are typically analyzed using standard regression, yet they reside on irregular domains which is a natural scenario for graph signal processing. To this end, we consider a market graph as an intuitive way to represent the relationships between financial assets. Traditional methods for estimating asset-return covariance operate under the assumption of statistical time-invariance, and are thus unable to appropriately infer the underlying true structure of the market graph. This work introduces a class of graph spectral estimators which cater for the nonstationarity inherent to asset price movements, and serve as a basis to represent the time-varying interactions between assets through a dynamic spectral market graph. Such an account of the time-varying nature of the asset-return covariance allows us to introduce the notion of dynamic spectral portfolio cuts, whereby the graph is partitioned into time-evolving clusters, allowing for online and robust asset allocation. The advantages of the proposed framework over traditional methods are demonstrated through numerical case studies using real-world price data.

Nonstationary Portfolios: Diversification in the Spectral Domain

Classical portfolio optimization methods typically determine an optimal capital allocation through the implicit, yet critical, assumption of statistical time-invariance. Such models are inadequate for real-world markets as they employ standard time-averaging based estimators which suffer significant information loss if the market observables are non-stationary. To this end, we reformulate the portfolio optimization problem in the spectral domain to cater for the nonstationarity inherent to asset price movements and, in this way, allow for optimal capital allocations to be time-varying. Unlike existing spectral portfolio techniques, the proposed framework employs augmented complex statistics in order to exploit the interactions between the real and imaginary parts of the complex spectral variables, which in turn allows for the modelling of both harmonics and cyclostationarity in the time domain. The advantages of the proposed framework over traditional methods are demonstrated through numerical simulations using real-world price data.

Graph Signal Processing -- Part III: Machine Learning on Graphs, from Graph Topology to Applications

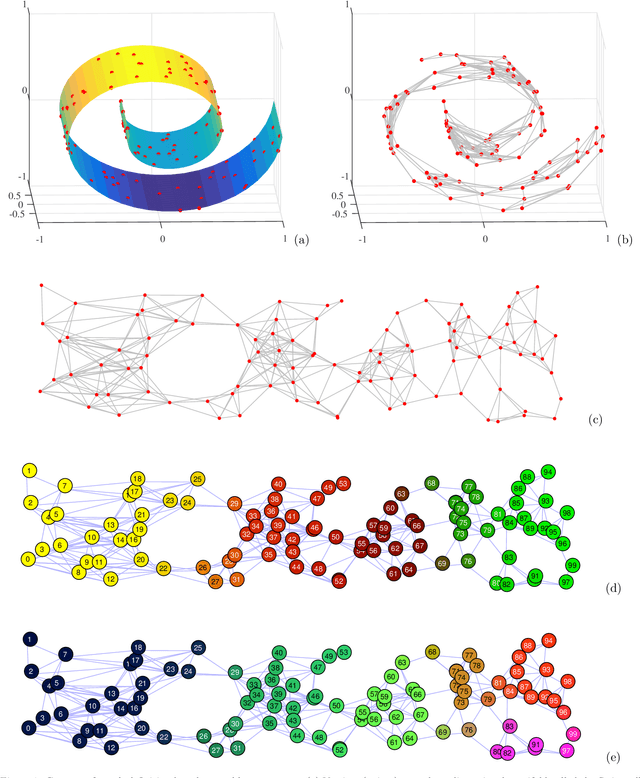
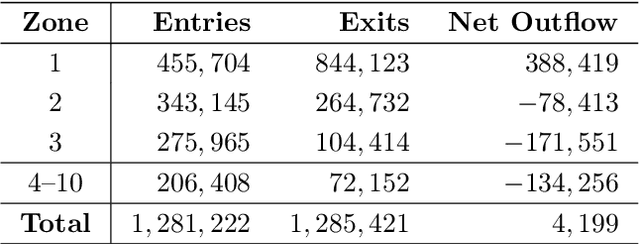
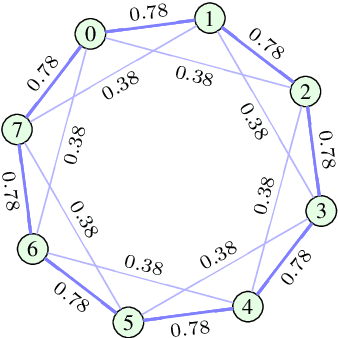
Many modern data analytics applications on graphs operate on domains where graph topology is not known a priori, and hence its determination becomes part of the problem definition, rather than serving as prior knowledge which aids the problem solution. Part III of this monograph starts by addressing ways to learn graph topology, from the case where the physics of the problem already suggest a possible topology, through to most general cases where the graph topology is learned from the data. A particular emphasis is on graph topology definition based on the correlation and precision matrices of the observed data, combined with additional prior knowledge and structural conditions, such as the smoothness or sparsity of graph connections. For learning sparse graphs (with small number of edges), the least absolute shrinkage and selection operator, known as LASSO is employed, along with its graph specific variant, graphical LASSO. For completeness, both variants of LASSO are derived in an intuitive way, and explained. An in-depth elaboration of the graph topology learning paradigm is provided through several examples on physically well defined graphs, such as electric circuits, linear heat transfer, social and computer networks, and spring-mass systems. As many graph neural networks (GNN) and convolutional graph networks (GCN) are emerging, we have also reviewed the main trends in GNNs and GCNs, from the perspective of graph signal filtering. Tensor representation of lattice-structured graphs is next considered, and it is shown that tensors (multidimensional data arrays) are a special class of graph signals, whereby the graph vertices reside on a high-dimensional regular lattice structure. This part of monograph concludes with two emerging applications in financial data processing and underground transportation networks modeling.