Neural Latent Geometry Search: Product Manifold Inference via Gromov-Hausdorff-Informed Bayesian Optimization

Recent research indicates that the performance of machine learning models can be improved by aligning the geometry of the latent space with the underlying data structure. Rather than relying solely on Euclidean space, researchers have proposed using hyperbolic and spherical spaces with constant curvature, or combinations thereof, to better model the latent space and enhance model performance. However, little attention has been given to the problem of automatically identifying the optimal latent geometry for the downstream task. We mathematically define this novel formulation and coin it as neural latent geometry search (NLGS). More specifically, we introduce a principled method that searches for a latent geometry composed of a product of constant curvature model spaces with minimal query evaluations. To accomplish this, we propose a novel notion of distance between candidate latent geometries based on the Gromov-Hausdorff distance from metric geometry. In order to compute the Gromov-Hausdorff distance, we introduce a mapping function that enables the comparison of different manifolds by embedding them in a common high-dimensional ambient space. Finally, we design a graph search space based on the calculated distances between candidate manifolds and use Bayesian optimization to search for the optimal latent geometry in a query-efficient manner. This is a general method which can be applied to search for the optimal latent geometry for a variety of models and downstream tasks. Extensive experiments on synthetic and real-world datasets confirm the efficacy of our method in identifying the optimal latent geometry for multiple machine learning problems.

Gromov-Hausdorff Distances for Comparing Product Manifolds of Model Spaces

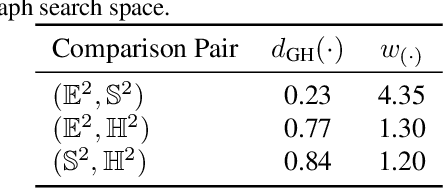
Recent studies propose enhancing machine learning models by aligning the geometric characteristics of the latent space with the underlying data structure. Instead of relying solely on Euclidean space, researchers have suggested using hyperbolic and spherical spaces with constant curvature, or their combinations (known as product manifolds), to improve model performance. However, there exists no principled technique to determine the best latent product manifold signature, which refers to the choice and dimensionality of manifold components. To address this, we introduce a novel notion of distance between candidate latent geometries using the Gromov-Hausdorff distance from metric geometry. We propose using a graph search space that uses the estimated Gromov-Hausdorff distances to search for the optimal latent geometry. In this work we focus on providing a description of an algorithm to compute the Gromov-Hausdorff distance between model spaces and its computational implementation.

Dynamic Portfolio Cuts: A Spectral Approach to Graph-Theoretic Diversification

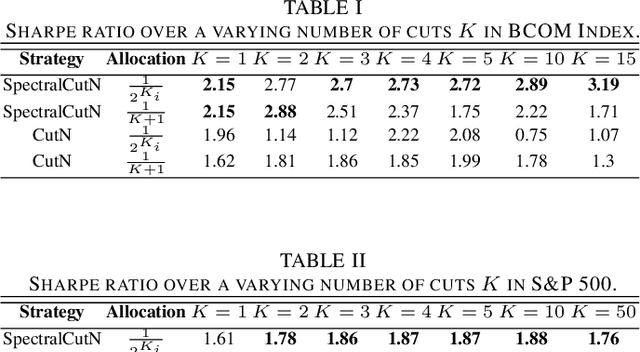
Stock market returns are typically analyzed using standard regression, yet they reside on irregular domains which is a natural scenario for graph signal processing. To this end, we consider a market graph as an intuitive way to represent the relationships between financial assets. Traditional methods for estimating asset-return covariance operate under the assumption of statistical time-invariance, and are thus unable to appropriately infer the underlying true structure of the market graph. This work introduces a class of graph spectral estimators which cater for the nonstationarity inherent to asset price movements, and serve as a basis to represent the time-varying interactions between assets through a dynamic spectral market graph. Such an account of the time-varying nature of the asset-return covariance allows us to introduce the notion of dynamic spectral portfolio cuts, whereby the graph is partitioned into time-evolving clusters, allowing for online and robust asset allocation. The advantages of the proposed framework over traditional methods are demonstrated through numerical case studies using real-world price data.

Nonstationary Portfolios: Diversification in the Spectral Domain

Classical portfolio optimization methods typically determine an optimal capital allocation through the implicit, yet critical, assumption of statistical time-invariance. Such models are inadequate for real-world markets as they employ standard time-averaging based estimators which suffer significant information loss if the market observables are non-stationary. To this end, we reformulate the portfolio optimization problem in the spectral domain to cater for the nonstationarity inherent to asset price movements and, in this way, allow for optimal capital allocations to be time-varying. Unlike existing spectral portfolio techniques, the proposed framework employs augmented complex statistics in order to exploit the interactions between the real and imaginary parts of the complex spectral variables, which in turn allows for the modelling of both harmonics and cyclostationarity in the time domain. The advantages of the proposed framework over traditional methods are demonstrated through numerical simulations using real-world price data.