Neural Latent Geometry Search: Product Manifold Inference via Gromov-Hausdorff-Informed Bayesian Optimization

Recent research indicates that the performance of machine learning models can be improved by aligning the geometry of the latent space with the underlying data structure. Rather than relying solely on Euclidean space, researchers have proposed using hyperbolic and spherical spaces with constant curvature, or combinations thereof, to better model the latent space and enhance model performance. However, little attention has been given to the problem of automatically identifying the optimal latent geometry for the downstream task. We mathematically define this novel formulation and coin it as neural latent geometry search (NLGS). More specifically, we introduce a principled method that searches for a latent geometry composed of a product of constant curvature model spaces with minimal query evaluations. To accomplish this, we propose a novel notion of distance between candidate latent geometries based on the Gromov-Hausdorff distance from metric geometry. In order to compute the Gromov-Hausdorff distance, we introduce a mapping function that enables the comparison of different manifolds by embedding them in a common high-dimensional ambient space. Finally, we design a graph search space based on the calculated distances between candidate manifolds and use Bayesian optimization to search for the optimal latent geometry in a query-efficient manner. This is a general method which can be applied to search for the optimal latent geometry for a variety of models and downstream tasks. Extensive experiments on synthetic and real-world datasets confirm the efficacy of our method in identifying the optimal latent geometry for multiple machine learning problems.

Gromov-Hausdorff Distances for Comparing Product Manifolds of Model Spaces

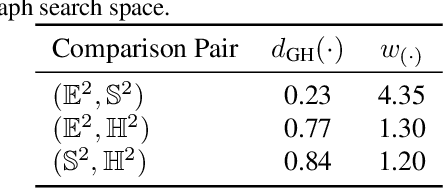
Recent studies propose enhancing machine learning models by aligning the geometric characteristics of the latent space with the underlying data structure. Instead of relying solely on Euclidean space, researchers have suggested using hyperbolic and spherical spaces with constant curvature, or their combinations (known as product manifolds), to improve model performance. However, there exists no principled technique to determine the best latent product manifold signature, which refers to the choice and dimensionality of manifold components. To address this, we introduce a novel notion of distance between candidate latent geometries using the Gromov-Hausdorff distance from metric geometry. We propose using a graph search space that uses the estimated Gromov-Hausdorff distances to search for the optimal latent geometry. In this work we focus on providing a description of an algorithm to compute the Gromov-Hausdorff distance between model spaces and its computational implementation.

Interpretability in deep learning for finance: a case study for the Heston model

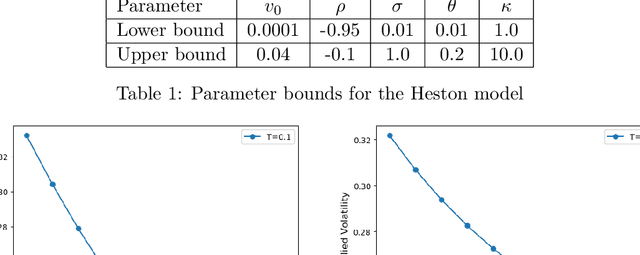
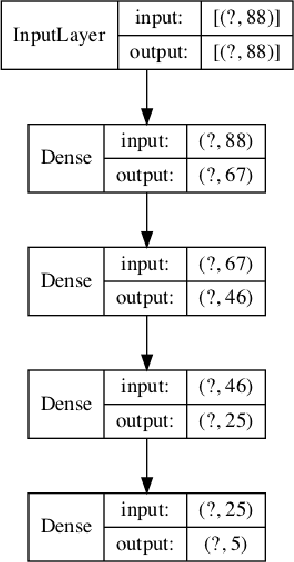
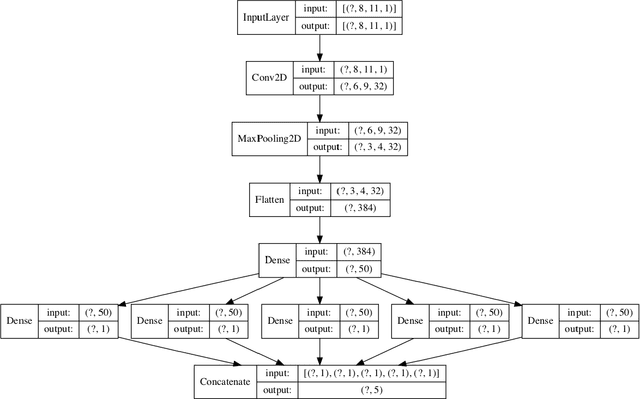
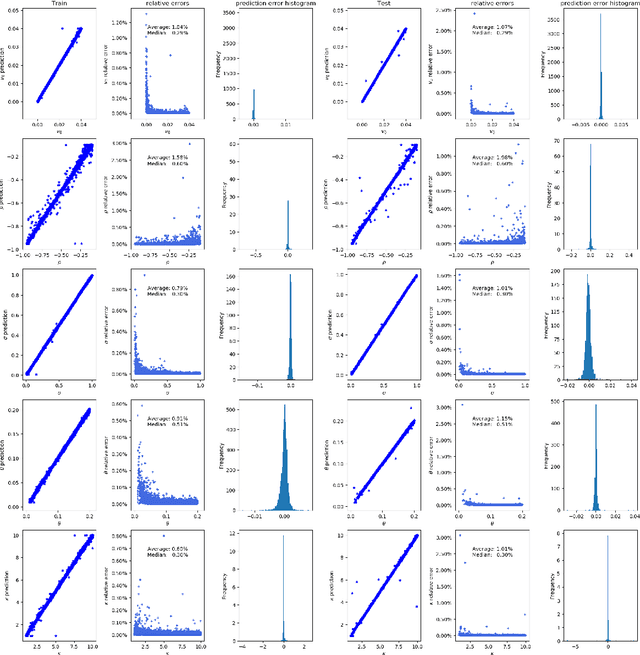
Deep learning is a powerful tool whose applications in quantitative finance are growing every day. Yet, artificial neural networks behave as black boxes and this hinders validation and accountability processes. Being able to interpret the inner functioning and the input-output relationship of these networks has become key for the acceptance of such tools. In this paper we focus on the calibration process of a stochastic volatility model, a subject recently tackled by deep learning algorithms. We analyze the Heston model in particular, as this model's properties are well known, resulting in an ideal benchmark case. We investigate the capability of local strategies and global strategies coming from cooperative game theory to explain the trained neural networks, and we find that global strategies such as Shapley values can be effectively used in practice. Our analysis also highlights that Shapley values may help choose the network architecture, as we find that fully-connected neural networks perform better than convolutional neural networks in predicting and interpreting the Heston model prices to parameters relationship.