Reinforcement learning for options on target volatility funds

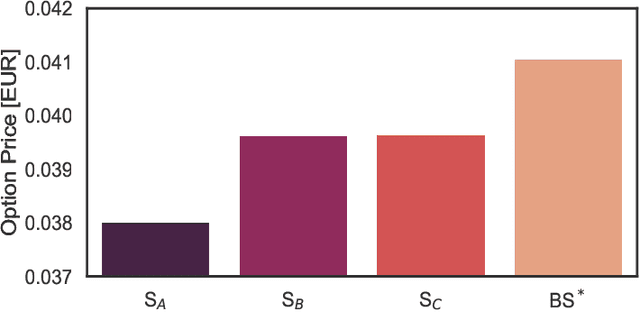
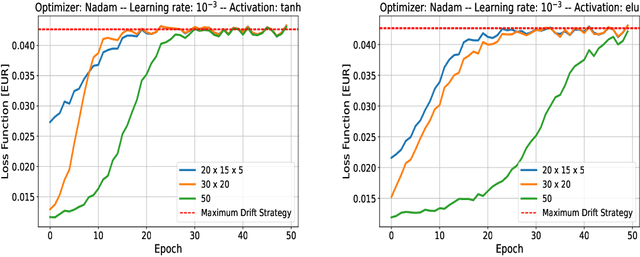
In this work we deal with the funding costs rising from hedging the risky securities underlying a target volatility strategy (TVS), a portfolio of risky assets and a risk-free one dynamically rebalanced in order to keep the realized volatility of the portfolio on a certain level. The uncertainty in the TVS risky portfolio composition along with the difference in hedging costs for each component requires to solve a control problem to evaluate the option prices. We derive an analytical solution of the problem in the Black and Scholes (BS) scenario. Then we use Reinforcement Learning (RL) techniques to determine the fund composition leading to the most conservative price under the local volatility (LV) model, for which an a priori solution is not available. We show how the performances of the RL agents are compatible with those obtained by applying path-wise the BS analytical strategy to the TVS dynamics, which therefore appears competitive also in the LV scenario.

Interpretability in deep learning for finance: a case study for the Heston model

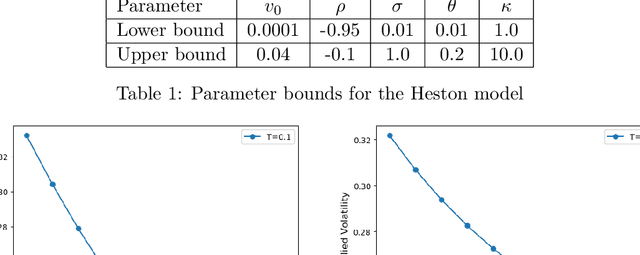
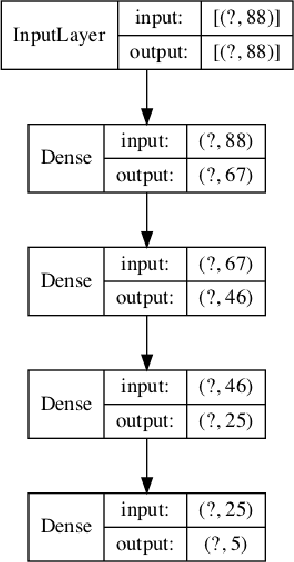
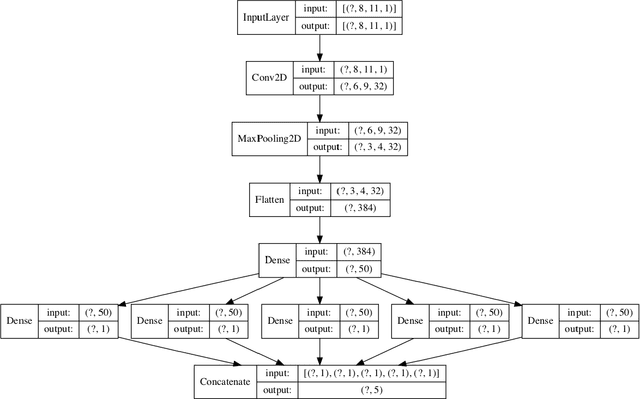
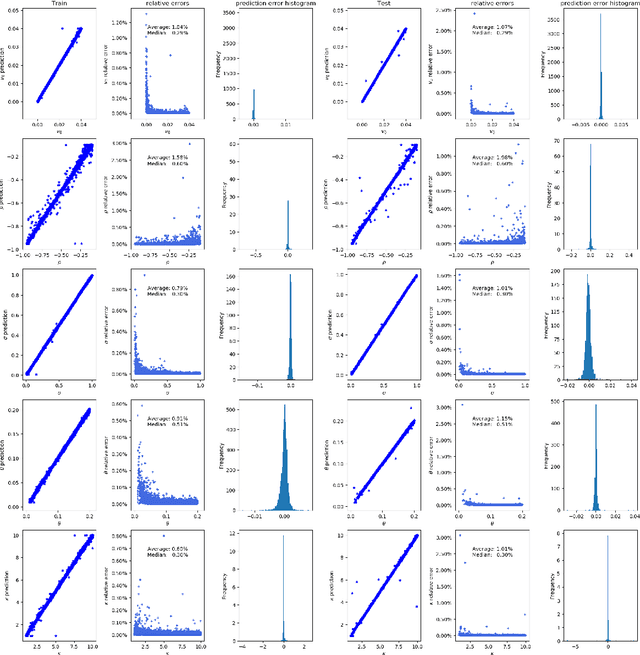
Deep learning is a powerful tool whose applications in quantitative finance are growing every day. Yet, artificial neural networks behave as black boxes and this hinders validation and accountability processes. Being able to interpret the inner functioning and the input-output relationship of these networks has become key for the acceptance of such tools. In this paper we focus on the calibration process of a stochastic volatility model, a subject recently tackled by deep learning algorithms. We analyze the Heston model in particular, as this model's properties are well known, resulting in an ideal benchmark case. We investigate the capability of local strategies and global strategies coming from cooperative game theory to explain the trained neural networks, and we find that global strategies such as Shapley values can be effectively used in practice. Our analysis also highlights that Shapley values may help choose the network architecture, as we find that fully-connected neural networks perform better than convolutional neural networks in predicting and interpreting the Heston model prices to parameters relationship.