Dynamic Portfolio Cuts: A Spectral Approach to Graph-Theoretic Diversification
Paper and Code
Jun 07, 2021


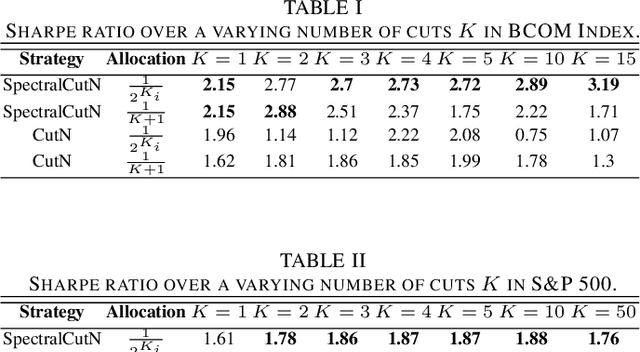
Stock market returns are typically analyzed using standard regression, yet they reside on irregular domains which is a natural scenario for graph signal processing. To this end, we consider a market graph as an intuitive way to represent the relationships between financial assets. Traditional methods for estimating asset-return covariance operate under the assumption of statistical time-invariance, and are thus unable to appropriately infer the underlying true structure of the market graph. This work introduces a class of graph spectral estimators which cater for the nonstationarity inherent to asset price movements, and serve as a basis to represent the time-varying interactions between assets through a dynamic spectral market graph. Such an account of the time-varying nature of the asset-return covariance allows us to introduce the notion of dynamic spectral portfolio cuts, whereby the graph is partitioned into time-evolving clusters, allowing for online and robust asset allocation. The advantages of the proposed framework over traditional methods are demonstrated through numerical case studies using real-world price data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge