Pearl: Parallel Evolutionary and Reinforcement Learning Library

Reinforcement learning is increasingly finding success across domains where the problem can be represented as a Markov decision process. Evolutionary computation algorithms have also proven successful in this domain, exhibiting similar performance to the generally more complex reinforcement learning. Whilst there exist many open-source reinforcement learning and evolutionary computation libraries, no publicly available library combines the two approaches for enhanced comparison, cooperation, or visualization. To this end, we have created Pearl (https://github.com/LondonNode/Pearl), an open source Python library designed to allow researchers to rapidly and conveniently perform optimized reinforcement learning, evolutionary computation and combinations of the two. The key features within Pearl include: modular and expandable components, opinionated module settings, Tensorboard integration, custom callbacks and comprehensive visualizations.

Graph Theory for Metro Traffic Modelling

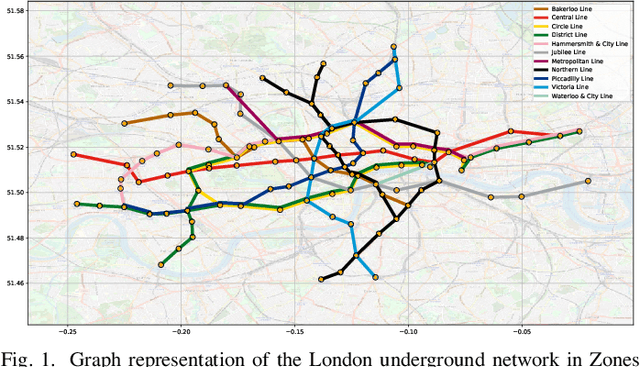
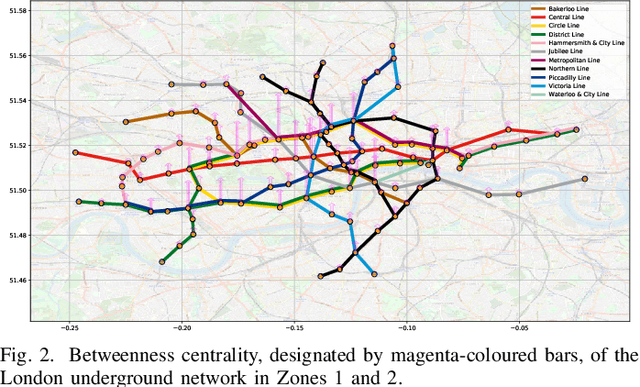
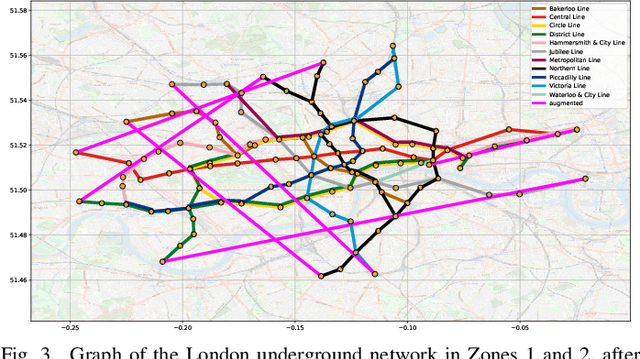
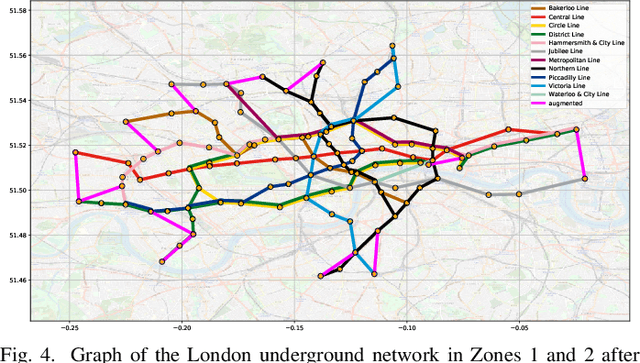
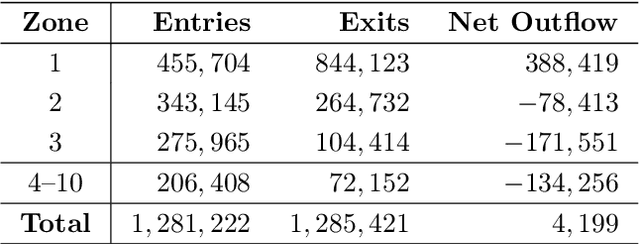
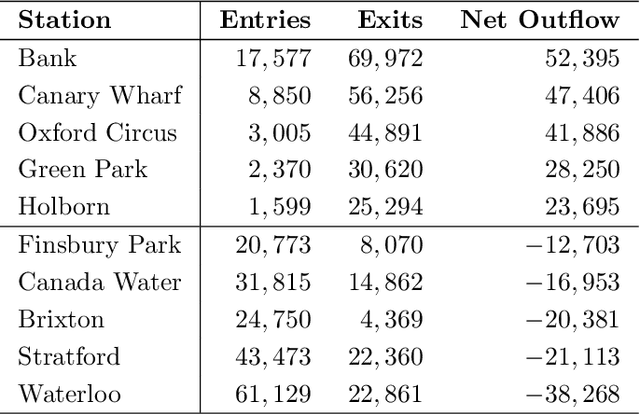
A unifying graph theoretic framework for the modelling of metro transportation networks is proposed. This is achieved by first introducing a basic graph framework for the modelling of the London underground system from a diffusion law point of view. This forms a basis for the analysis of both station importance and their vulnerability, whereby the concept of graph vertex centrality plays a key role. We next explore k-edge augmentation of a graph topology, and illustrate its usefulness both for improving the network robustness and as a planning tool. Upon establishing the graph theoretic attributes of the underlying graph topology, we proceed to introduce models for processing data on such a metro graph. Commuter movement is shown to obey the Fick's law of diffusion, where the graph Laplacian provides an analytical model for the diffusion process of commuter population dynamics. Finally, we also explore the application of modern deep learning models, such as graph neural networks and hyper-graph neural networks, as general purpose models for the modelling and forecasting of underground data, especially in the context of the morning and evening rush hours. Comprehensive simulations including the passenger in- and out-flows during the morning rush hour in London demonstrates the advantages of the graph models in metro planning and traffic management, a formal mathematical approach with wide economic implications.

Graph Signal Processing -- Part III: Machine Learning on Graphs, from Graph Topology to Applications

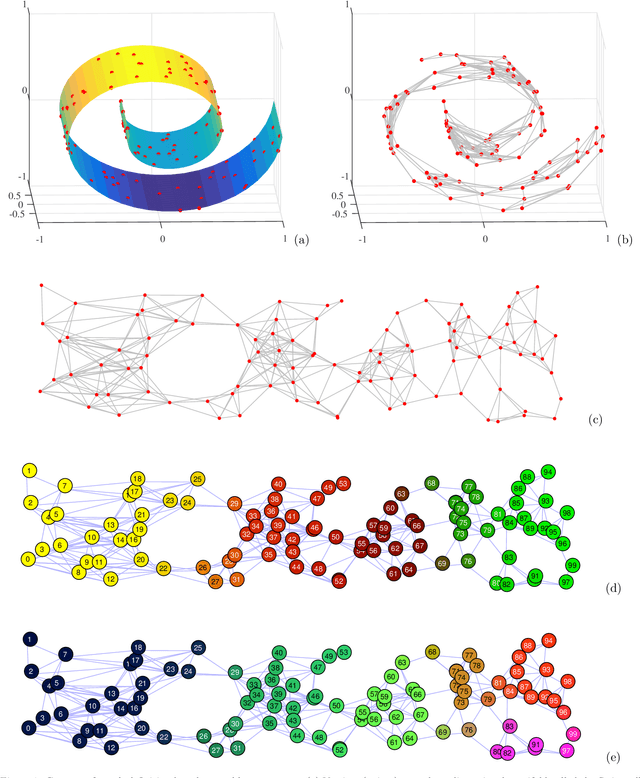
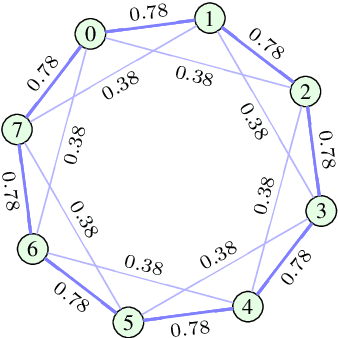
Many modern data analytics applications on graphs operate on domains where graph topology is not known a priori, and hence its determination becomes part of the problem definition, rather than serving as prior knowledge which aids the problem solution. Part III of this monograph starts by addressing ways to learn graph topology, from the case where the physics of the problem already suggest a possible topology, through to most general cases where the graph topology is learned from the data. A particular emphasis is on graph topology definition based on the correlation and precision matrices of the observed data, combined with additional prior knowledge and structural conditions, such as the smoothness or sparsity of graph connections. For learning sparse graphs (with small number of edges), the least absolute shrinkage and selection operator, known as LASSO is employed, along with its graph specific variant, graphical LASSO. For completeness, both variants of LASSO are derived in an intuitive way, and explained. An in-depth elaboration of the graph topology learning paradigm is provided through several examples on physically well defined graphs, such as electric circuits, linear heat transfer, social and computer networks, and spring-mass systems. As many graph neural networks (GNN) and convolutional graph networks (GCN) are emerging, we have also reviewed the main trends in GNNs and GCNs, from the perspective of graph signal filtering. Tensor representation of lattice-structured graphs is next considered, and it is shown that tensors (multidimensional data arrays) are a special class of graph signals, whereby the graph vertices reside on a high-dimensional regular lattice structure. This part of monograph concludes with two emerging applications in financial data processing and underground transportation networks modeling.