Graph Theory for Metro Traffic Modelling

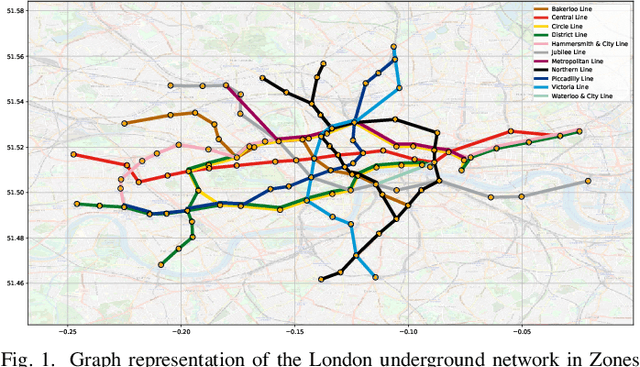
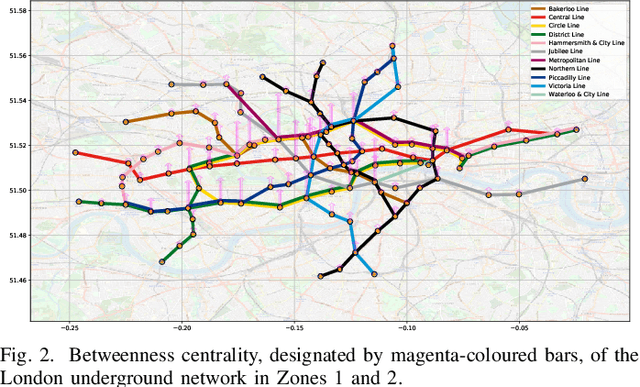
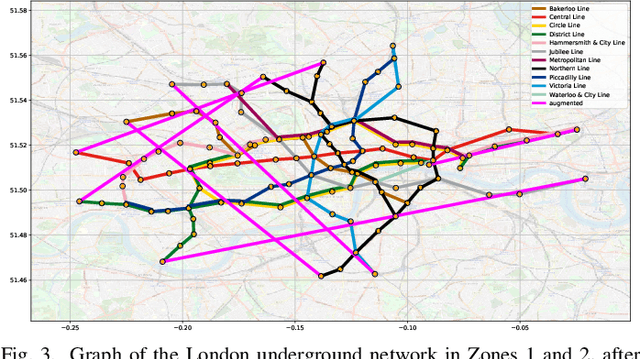
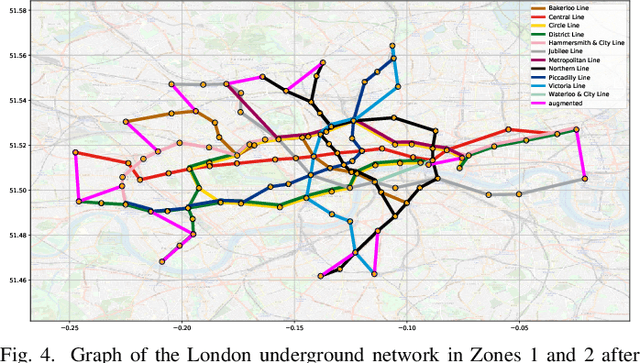
A unifying graph theoretic framework for the modelling of metro transportation networks is proposed. This is achieved by first introducing a basic graph framework for the modelling of the London underground system from a diffusion law point of view. This forms a basis for the analysis of both station importance and their vulnerability, whereby the concept of graph vertex centrality plays a key role. We next explore k-edge augmentation of a graph topology, and illustrate its usefulness both for improving the network robustness and as a planning tool. Upon establishing the graph theoretic attributes of the underlying graph topology, we proceed to introduce models for processing data on such a metro graph. Commuter movement is shown to obey the Fick's law of diffusion, where the graph Laplacian provides an analytical model for the diffusion process of commuter population dynamics. Finally, we also explore the application of modern deep learning models, such as graph neural networks and hyper-graph neural networks, as general purpose models for the modelling and forecasting of underground data, especially in the context of the morning and evening rush hours. Comprehensive simulations including the passenger in- and out-flows during the morning rush hour in London demonstrates the advantages of the graph models in metro planning and traffic management, a formal mathematical approach with wide economic implications.

Robust Principal Component Analysis Based On Maximum Correntropy Power Iterations

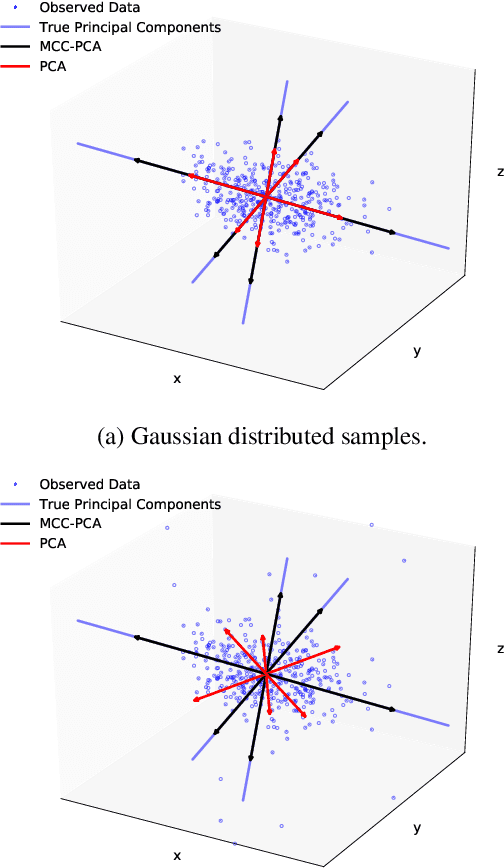
Principal component analysis (PCA) is recognised as a quintessential data analysis technique when it comes to describing linear relationships between the features of a dataset. However, the well-known sensitivity of PCA to non-Gaussian samples and/or outliers often makes it unreliable in practice. To this end, a robust formulation of PCA is derived based on the maximum correntropy criterion (MCC) so as to maximise the expected likelihood of Gaussian distributed reconstruction errors. In this way, the proposed solution reduces to a generalised power iteration, whereby: (i) robust estimates of the principal components are obtained even in the presence of outliers; (ii) the number of principal components need not be specified in advance; and (iii) the entire set of principal components can be obtained, unlike existing approaches. The advantages of the proposed maximum correntropy power iteration (MCPI) are demonstrated through an intuitive numerical example.