A general solver to the elliptical mixture model through an approximate Wasserstein manifold

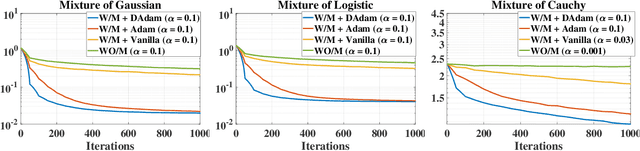
This paper studies the problem of estimation for general finite mixture models, with a particular focus on the elliptical mixture models (EMMs). Instead of using the widely adopted Kullback-Leibler divergence, we provide a stable solution to the EMMs that is robust to initialisations and attains superior local optimum by adaptively optimising along a manifold of an approximate Wasserstein distance. More specifically, we first summarise computable and identifiable EMMs, in order to identify the optimisation problem. Due to a probability constraint, solving this problem is cumbersome and unstable, especially under the Wasserstein distance. We thus resort to an efficient optimisation on a statistical manifold defined under an approximate Wasserstein distance, which allows for explicit metrics and operations. This is shown to significantly stabilise and improve the EMM estimations. We also propose an adaptive method to further accelerate the convergence. Experimental results demonstrate excellent performances of the proposed solver.