Learning to Manage Investment Portfolios beyond Simple Utility Functions

While investment funds publicly disclose their objectives in broad terms, their managers optimize for complex combinations of competing goals that go beyond simple risk-return trade-offs. Traditional approaches attempt to model this through multi-objective utility functions, but face fundamental challenges in specification and parameterization. We propose a generative framework that learns latent representations of fund manager strategies without requiring explicit utility specification. Our approach directly models the conditional probability of a fund's portfolio weights, given stock characteristics, historical returns, previous weights, and a latent variable representing the fund's strategy. Unlike methods based on reinforcement learning or imitation learning, which require specified rewards or labeled expert objectives, our GAN-based architecture learns directly from the joint distribution of observed holdings and market data. We validate our framework on a dataset of 1436 U.S. equity mutual funds. The learned representations successfully capture known investment styles, such as "growth" and "value," while also revealing implicit manager objectives. For instance, we find that while many funds exhibit characteristics of Markowitz-like optimization, they do so with heterogeneous realizations for turnover, concentration, and latent factors. To analyze and interpret the end-to-end model, we develop a series of tests that explain the model, and we show that the benchmark's expert labeling are contained in our model's encoding in a linear interpretable way. Our framework provides a data-driven approach for characterizing investment strategies for applications in market simulation, strategy attribution, and regulatory oversight.

Capacity Planning and Scheduling for Jobs with Uncertainty in Resource Usage and Duration

Organizations around the world schedule jobs (programs) regularly to perform various tasks dictated by their end users. With the major movement towards using a cloud computing infrastructure, our organization follows a hybrid approach with both cloud and on-prem servers. The objective of this work is to perform capacity planning, i.e., estimate resource requirements, and job scheduling for on-prem grid computing environments. A key contribution of our approach is handling uncertainty in both resource usage and duration of the jobs, a critical aspect in the finance industry where stochastic market conditions significantly influence job characteristics. For capacity planning and scheduling, we simultaneously balance two conflicting objectives: (a) minimize resource usage, and (b) provide high quality-of-service to the end users by completing jobs by their requested deadlines. We propose approximate approaches using deterministic estimators and pair sampling-based constraint programming. Our best approach (pair sampling-based) achieves much lower peak resource usage compared to manual scheduling without compromising on the quality-of-service.

Entropy-Aware Branching for Improved Mathematical Reasoning

While Large Language Models (LLMs) are effectively aligned through extensive pre-training and fine-tuning, they still struggle with varying levels of uncertainty during token generation. In our investigation of mathematical reasoning, we observe that errors are more likely to arise at tokens exhibiting high entropy and variance of entropy in the model's output distribution. Based on the observation, we propose a novel approach that dynamically branches the generation process on demand instead of defaulting to the single most probable token. By exploring in parallel multiple branches stemming from high probability tokens of critical decision points, the model can discover diverse reasoning paths that might otherwise be missed. We further harness external feedback from larger models to rank and select the most coherent and accurate reasoning branch. Our experimental results on mathematical word problems and calculation questions show that this branching strategy boosts the reasoning capabilities of small LLMs up to 4.6% compared to conventional argmax decoding.

How Robust are Limit Order Book Representations under Data Perturbation?

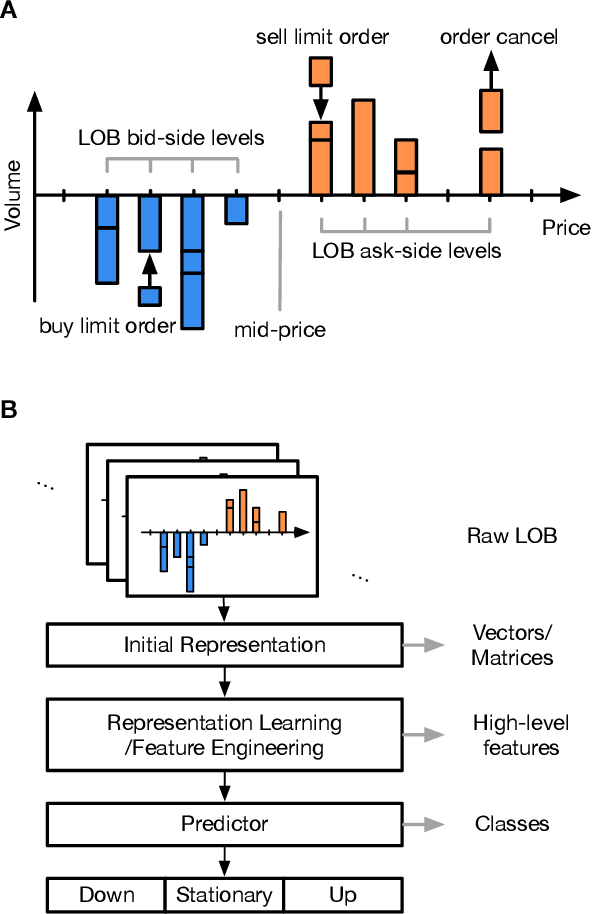
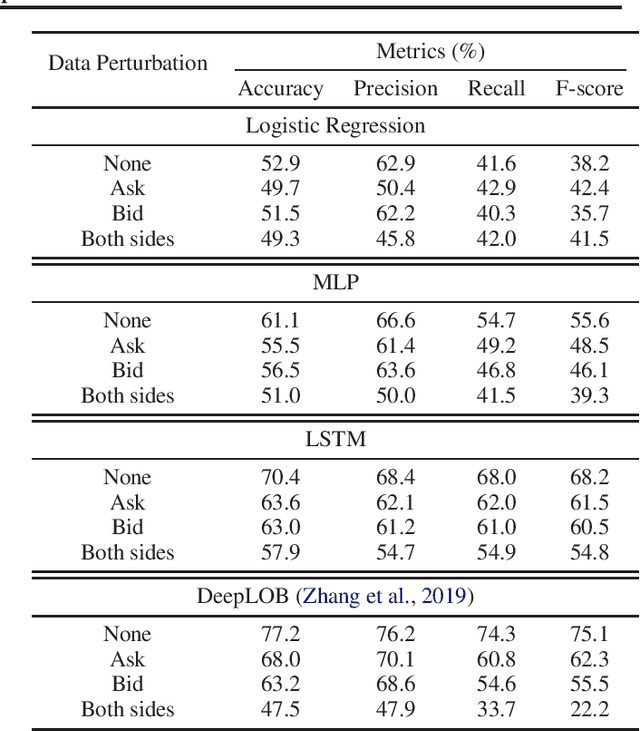
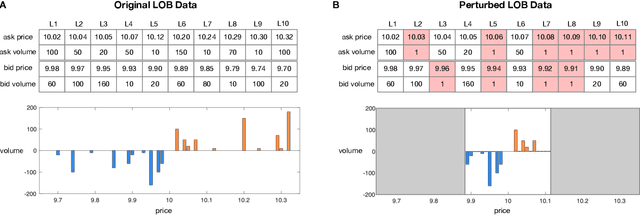
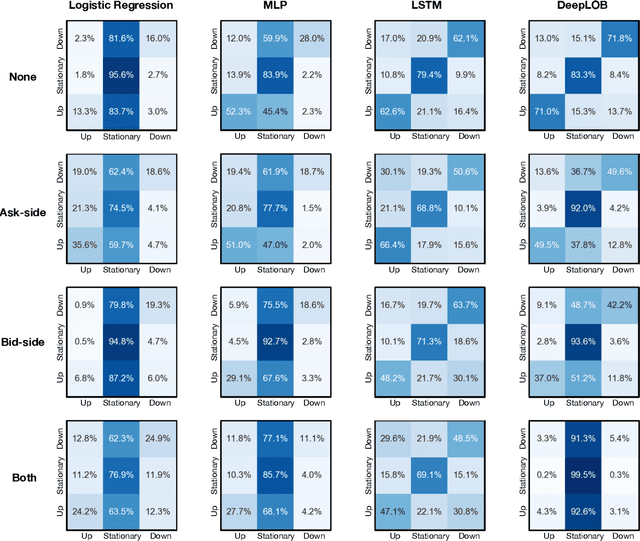
The success of machine learning models in the financial domain is highly reliant on the quality of the data representation. In this paper, we focus on the representation of limit order book data and discuss the opportunities and challenges for learning representations of such data. We also experimentally analyse the issues associated with existing representations and present a guideline for future research in this area.

A Framework for Institutional Risk Identification using Knowledge Graphs and Automated News Profiling

Organizations around the world face an array of risks impacting their operations globally. It is imperative to have a robust risk identification process to detect and evaluate the impact of potential risks before they materialize. Given the nature of the task and the current requirements of deep subject matter expertise, most organizations utilize a heavily manual process. In our work, we develop an automated system that (a) continuously monitors global news, (b) is able to autonomously identify and characterize risks, (c) is able to determine the proximity of reaching triggers to determine the distance from the manifestation of the risk impact and (d) identifies organization's operational areas that may be most impacted by the risk. Other contributions also include: (a) a knowledge graph representation of risks and (b) relevant news matching to risks identified by the organization utilizing a neural embedding model to match the textual description of a given risk with multi-lingual news.

Tucker Tensor Layer in Fully Connected Neural Networks

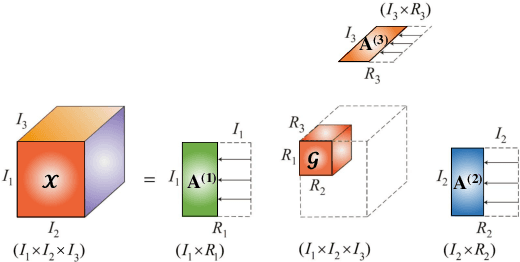
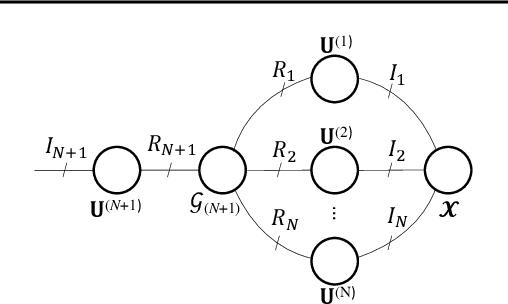
We introduce the Tucker Tensor Layer (TTL), an alternative to the dense weight-matrices of the fully connected layers of feed-forward neural networks (NNs), to answer the long standing quest to compress NNs and improve their interpretability. This is achieved by treating these weight-matrices as the unfolding of a higher order weight-tensor. This enables us to introduce a framework for exploiting the multi-way nature of the weight-tensor in order to efficiently reduce the number of parameters, by virtue of the compression properties of tensor decompositions. The Tucker Decomposition (TKD) is employed to decompose the weight-tensor into a core tensor and factor matrices. We re-derive back-propagation within this framework, by extending the notion of matrix derivatives to tensors. In this way, the physical interpretability of the TKD is exploited to gain insights into training, through the process of computing gradients with respect to each factor matrix. The proposed framework is validated on synthetic data and on the Fashion-MNIST dataset, emphasizing the relative importance of various data features in training, hence mitigating the "black-box" issue inherent to NNs. Experiments on both MNIST and Fashion-MNIST illustrate the compression properties of the TTL, achieving a 66.63 fold compression whilst maintaining comparable performance to the uncompressed NN.