Divide-and-Conquer: Towards Generalizable Amortized Bayesian Inference for the Drift Diffusion Model

The drift diffusion model (DDM) is a cornerstone of cognitive decision-making research. Although numerous estimation methods exist, researchers continue to seek inference approaches that are both fast and flexible across diverse study designs. Amortized Bayesian inference (ABI) can provide nearly instantaneous inference for complex stochastic models like the DDM, but neural networks trained for one study design cannot generalize to others. In this paper, we propose a divide-and-conquer framework that address this limitation. The core idea is that the DDM's independence assumption allows the full dataset to be decomposed into pairwise shards, each sharing a common structure that a single neural network can learn. Inference is performed on each shard separately and the resulting posteriors are combined via consensus MCMC to approximate the full posterior. Using simulated datasets, we evaluate the accuracy and uncertainty of this method. Our results show that the proposed divide-and-conquer approach achieves accuracy and uncertainty comparable to MCMC while reducing computational cost by several orders of magnitude. This work not only advances DDM estimation but also demonstrates a general strategy for improving the scalability and generalizability of ABI methods across diverse applications.

Understanding Guest Preferences and Optimizing Two-sided Marketplaces: Airbnb as an Example

Airbnb is a community based on connection and belonging -- many hosts on Airbnb are everyday people who share their worlds to provide guests with the feeling of connection and being at home; Airbnb strives to connect people and places. Among our efforts to connect guests and hosts, we provide tools to enable hosts to set competitive prices, which helps improve affordability for guests while helping hosts get more bookings. We also personalize the guest experience to show them the listings that match their needs. To help inform these efforts, we combine economic modeling and causal inference techniques to understand how guests book stays based on the prices hosts set, among other factors, and how that preference varies across different guests and listings. Such understanding helps us identify opportunities for Airbnb to support the marketplace and better connect guests and hosts. For example, understanding how much guests respond to different prices helps optimize the tools that we provide to hosts, in order to enable hosts to choose and set competitive prices that further balance demand and supply. As another example, understanding heterogeneity in guest preferences helps us personalize the guest experience and better match them with the listings that meet their needs, based on how much they respond to different prices and other factors.

Hierarchical Clustering As a Novel Solution to the Notorious Multicollinearity Problem in Observational Causal Inference

Multicollinearity is a long lasting challenge in observational causal inference, especially in regressions -- highly correlated independent variables make it hard to isolate their individual impacts on outcomes of interest. While common solutions such as shrinkage estimators and principal component regressions are helpful in prediction problems, a crucial limitation hinders their applicability to causal inference problems -- they cannot provide the original causal relationships. To fill the gap, we present an innovative and intuitive solution, by employing hierarchical clustering to aggregate data in a way that effectively alleviates collinearity. This method is generally applicable to causal problems featuring multicollinearity. We use a marketing application to demonstrate how and why it works. Expenditures on different advertising channels often exhibit correlations, making it exceedingly difficult to separately measure their impact. Many previous studies proposed to leverage granular cross-sectional data for better identification but, to our knowledge, none explicitly addressed multicollinearity, which undermines causal identification even with granular data. We propose to hierarchically cluster geographic units based on marketing spend correlation to reduce collinearity, and to implement a Bayesian Marketing Mix Model with cluster-level data. Such clustering happens in two steps -- we first normalize and demean geo-level data to establish a common scale and to eliminate the common trends; we then calculate pairwise distance to summarize marketing spend correlation between geos and cluster the ones with moderate to strong correlation. Both descriptive evidence and regression analysis affirm that such hierarchical clustering effectively mitigates collinearity and facilitates the separate identification of the impact of different marketing channels.

Estimating Supply Incrementality in Two-sided Marketplaces: A Causal Machine Learning Approach

In two-sided marketplaces with heterogeneous products, it is important to understand the causal relationship between additional supply and marketplace outcomes, such as the total quantity transacted or transaction value in the marketplace. This paper studies a causal machine learning approach to estimating this relationship across product segments. We use the Airbnb marketplace as an example, focusing on the impact of additional listing supply on total bookings, but the methodology applies to other two-sided marketplaces. Our approach combines double/debiased machine learning with a hierarchical Bayesian framework that leverages pre-existing knowledge as priors. We construct tractable and informative features for the model by leveraging measures of product segment similarity from the geospatial literature. We find that such a model provides plausible estimates of the marketplace returns to additional supply and strong out of sample performance.

Personalizing Marketplace Policies with Competing Objectives and Constrained Experiments: Evidence from a Job Marketplace

Two-sided marketplaces connect distinct user groups whose interests often conflict -- improving outcomes on one side could degrade the other side's experience. To address this challenge, we deploy an integrated framework for personalizing free-value thresholds -- a policy governing the scope of complimentary services for job listings -- across a two-sided job marketplace connecting millions of employers and job seekers. Our personalized policy delivers statistically significant and economically sizable lift in the target metric while respecting engagement guardrail constraints. Direct application of standard uplift methods proves insufficient here for two reasons. First, cross-side externalities demand multi-objective optimization: maximizing employer-side metrics risks harming job seeker engagement, with effects varying substantially across job segments. Second, marketplace interference necessitates cluster-level randomization, limiting us to few discrete treatment levels -- effectively a form of positivity violation that rules out methods designed for continuous treatments. We contribute an integrated framework with three components. Our ensemble-based hybrid ranking models target and guardrail metrics separately, cutting guardrail risk by over 10% for equivalent target gains compared to single-objective approaches. A treatment effect extrapolation method extends our estimates from limited experimental variation to untested policy levels, relying on monotonicity assumptions that we validate empirically. Finally, we present production deployment, where post-launch data confirms both extrapolation accuracy and guardrail compliance. Our deployed system demonstrates that principled methodology can enable meaningful personalization even when experiments are severely constrained and different objectives compete -- common conditions that characterize many real-world marketplaces.

The Subset Sum Matching Problem

This paper presents a new combinatorial optimisation task, the Subset Sum Matching Problem (SSMP), which is an abstraction of common financial applications such as trades reconciliation. We present three algorithms, two suboptimal and one optimal, to solve this problem. We also generate a benchmark to cover different instances of SSMP varying in complexity, and carry out an experimental evaluation to assess the performance of the approaches.

LENS: Multi-level Evaluation of Multimodal Reasoning with Large Language Models

Multimodal Large Language Models (MLLMs) have achieved significant advances in integrating visual and linguistic information, yet their ability to reason about complex and real-world scenarios remains limited. The existing benchmarks are usually constructed in the task-oriented manner without guarantee that different task samples come from the same data distribution, thus they often fall short in evaluating the synergistic effects of lower-level perceptual capabilities on higher-order reasoning. To lift this limitation, we contribute Lens, a multi-level benchmark with 3.4K contemporary images and 60K+ human-authored questions covering eight tasks and 12 daily scenarios, forming three progressive task tiers, i.e., perception, understanding, and reasoning. One feature is that each image is equipped with rich annotations for all tasks. Thus, this dataset intrinsically supports to evaluate MLLMs to handle image-invariable prompts, from basic perception to compositional reasoning. In addition, our images are manully collected from the social media, in which 53% were published later than Jan. 2025. We evaluate 15+ frontier MLLMs such as Qwen2.5-VL-72B, InternVL3-78B, GPT-4o and two reasoning models QVQ-72B-preview and Kimi-VL. These models are released later than Dec. 2024, and none of them achieve an accuracy greater than 60% in the reasoning tasks. Project page: https://github.com/Lens4MLLMs/lens. ICCV 2025 workshop page: https://lens4mllms.github.io/mars2-workshop-iccv2025/

Testing and Improving the Robustness of Amortized Bayesian Inference for Cognitive Models

Contaminant observations and outliers often cause problems when estimating the parameters of cognitive models, which are statistical models representing cognitive processes. In this study, we test and improve the robustness of parameter estimation using amortized Bayesian inference (ABI) with neural networks. To this end, we conduct systematic analyses on a toy example and analyze both synthetic and real data using a popular cognitive model, the Drift Diffusion Models (DDM). First, we study the sensitivity of ABI to contaminants with tools from robust statistics: the empirical influence function and the breakdown point. Next, we propose a data augmentation or noise injection approach that incorporates a contamination distribution into the data-generating process during training. We examine several candidate distributions and evaluate their performance and cost in terms of accuracy and efficiency loss relative to a standard estimator. Introducing contaminants from a Cauchy distribution during training considerably increases the robustness of the neural density estimator as measured by bounded influence functions and a much higher breakdown point. Overall, the proposed method is straightforward and practical to implement and has a broad applicability in fields where outlier detection or removal is challenging.

Abstract Visual Reasoning: An Algebraic Approach for Solving Raven's Progressive Matrices

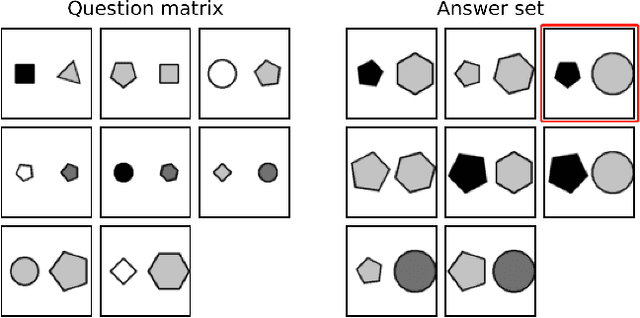
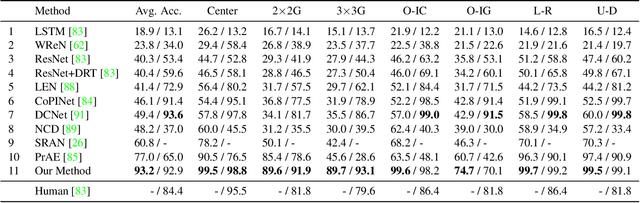
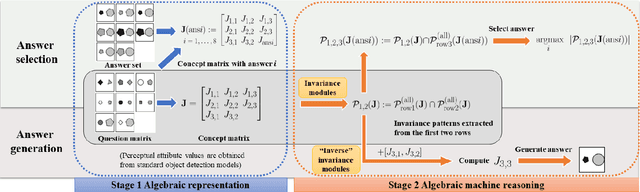
We introduce algebraic machine reasoning, a new reasoning framework that is well-suited for abstract reasoning. Effectively, algebraic machine reasoning reduces the difficult process of novel problem-solving to routine algebraic computation. The fundamental algebraic objects of interest are the ideals of some suitably initialized polynomial ring. We shall explain how solving Raven's Progressive Matrices (RPMs) can be realized as computational problems in algebra, which combine various well-known algebraic subroutines that include: Computing the Gr\"obner basis of an ideal, checking for ideal containment, etc. Crucially, the additional algebraic structure satisfied by ideals allows for more operations on ideals beyond set-theoretic operations. Our algebraic machine reasoning framework is not only able to select the correct answer from a given answer set, but also able to generate the correct answer with only the question matrix given. Experiments on the I-RAVEN dataset yield an overall $93.2\%$ accuracy, which significantly outperforms the current state-of-the-art accuracy of $77.0\%$ and exceeds human performance at $84.4\%$ accuracy.

How Robust are Limit Order Book Representations under Data Perturbation?

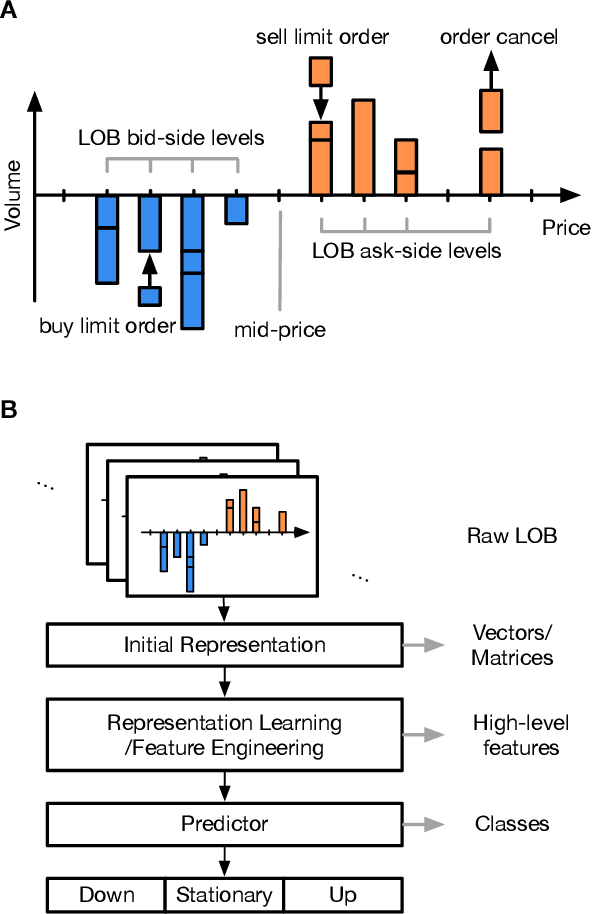
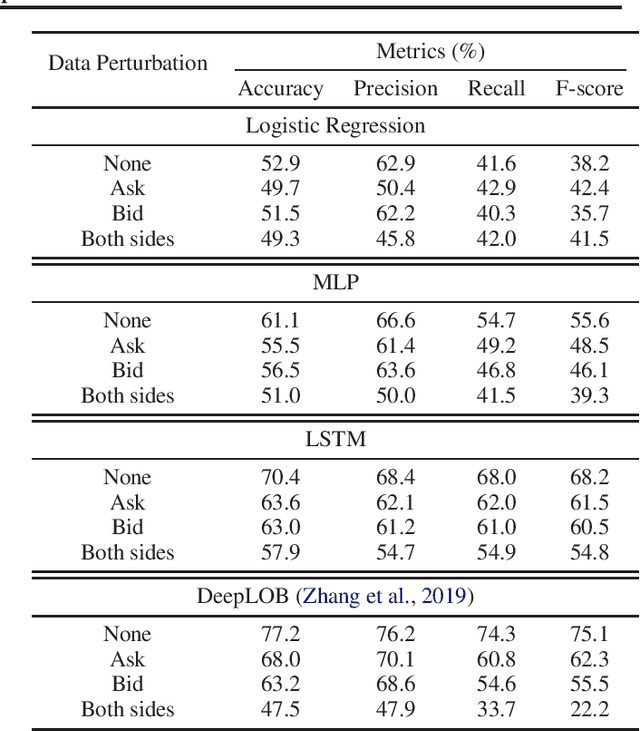
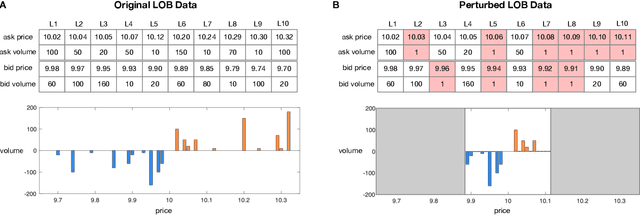
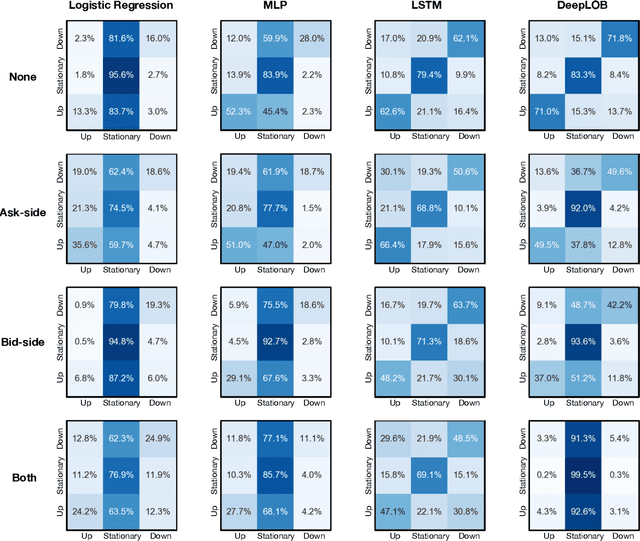
The success of machine learning models in the financial domain is highly reliant on the quality of the data representation. In this paper, we focus on the representation of limit order book data and discuss the opportunities and challenges for learning representations of such data. We also experimentally analyse the issues associated with existing representations and present a guideline for future research in this area.