Spectral Co-Distillation for Personalized Federated Learning

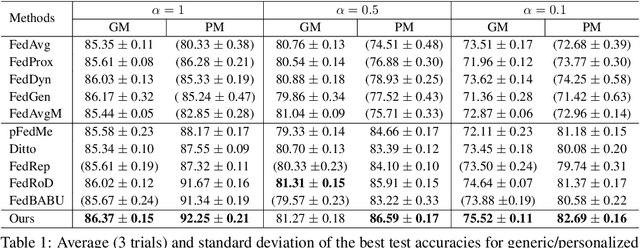
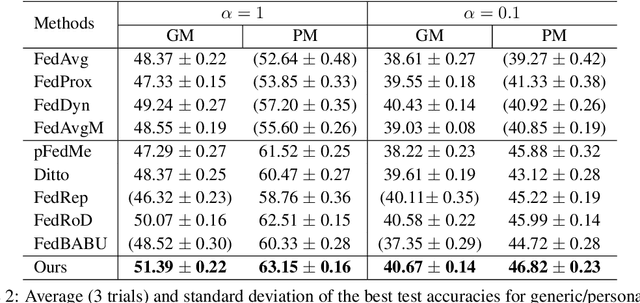
Personalized federated learning (PFL) has been widely investigated to address the challenge of data heterogeneity, especially when a single generic model is inadequate in satisfying the diverse performance requirements of local clients simultaneously. Existing PFL methods are inherently based on the idea that the relations between the generic global and personalized local models are captured by the similarity of model weights. Such a similarity is primarily based on either partitioning the model architecture into generic versus personalized components, or modeling client relationships via model weights. To better capture similar (yet distinct) generic versus personalized model representations, we propose \textit{spectral distillation}, a novel distillation method based on model spectrum information. Building upon spectral distillation, we also introduce a co-distillation framework that establishes a two-way bridge between generic and personalized model training. Moreover, to utilize the local idle time in conventional PFL, we propose a wait-free local training protocol. Through extensive experiments on multiple datasets over diverse heterogeneous data settings, we demonstrate the outperformance and efficacy of our proposed spectral co-distillation method, as well as our wait-free training protocol.

The Role of Federated Learning in a Wireless World with Foundation Models

Foundation models (FMs) are general-purpose artificial intelligence (AI) models that have recently enabled multiple brand-new generative AI applications. The rapid advances in FMs serve as an important contextual backdrop for the vision of next-generation wireless networks, where federated learning (FL) is a key enabler of distributed network intelligence. Currently, the exploration of the interplay between FMs and FL is still in its nascent stage. Naturally, FMs are capable of boosting the performance of FL, and FL could also leverage decentralized data and computing resources to assist in the training of FMs. However, the exceptionally high requirements that FMs have for computing resources, storage, and communication overhead would pose critical challenges to FL-enabled wireless networks. In this article, we explore the extent to which FMs are suitable for FL over wireless networks, including a broad overview of research challenges and opportunities. In particular, we discuss multiple new paradigms for realizing future intelligent networks that integrate FMs and FL. We also consolidate several broad research directions associated with these paradigms.

GenKL: An Iterative Framework for Resolving Label Ambiguity and Label Non-conformity in Web Images Via a New Generalized KL Divergence

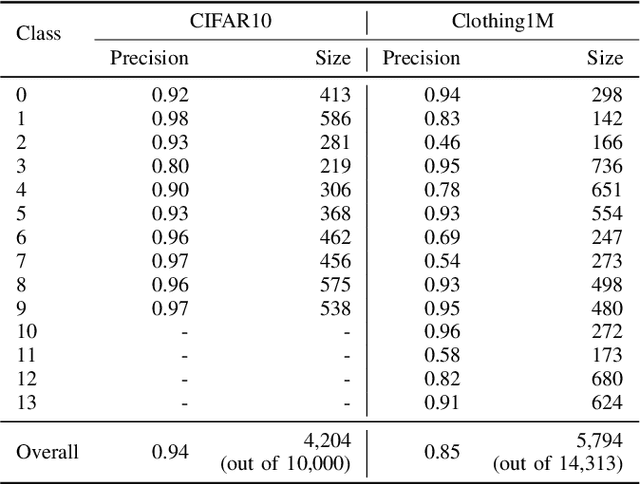
Web image datasets curated online inherently contain ambiguous in-distribution (ID) instances and out-of-distribution (OOD) instances, which we collectively call non-conforming (NC) instances. In many recent approaches for mitigating the negative effects of NC instances, the core implicit assumption is that the NC instances can be found via entropy maximization. For "entropy" to be well-defined, we are interpreting the output prediction vector of an instance as the parameter vector of a multinomial random variable, with respect to some trained model with a softmax output layer. Hence, entropy maximization is based on the idealized assumption that NC instances have predictions that are "almost" uniformly distributed. However, in real-world web image datasets, there are numerous NC instances whose predictions are far from being uniformly distributed. To tackle the limitation of entropy maximization, we propose $(\alpha, \beta)$-generalized KL divergence, $\mathcal{D}_{\text{KL}}^{\alpha, \beta}(p\|q)$, which can be used to identify significantly more NC instances. Theoretical properties of $\mathcal{D}_{\text{KL}}^{\alpha, \beta}(p\|q)$ are proven, and we also show empirically that a simple use of $\mathcal{D}_{\text{KL}}^{\alpha, \beta}(p\|q)$ outperforms all baselines on the NC instance identification task. Building upon $(\alpha,\beta)$-generalized KL divergence, we also introduce a new iterative training framework, GenKL, that identifies and relabels NC instances. When evaluated on three web image datasets, Clothing1M, Food101/Food101N, and mini WebVision 1.0, we achieved new state-of-the-art classification accuracies: $81.34\%$, $85.73\%$ and $78.99\%$/$92.54\%$ (top-1/top-5), respectively.

Abstract Visual Reasoning: An Algebraic Approach for Solving Raven's Progressive Matrices

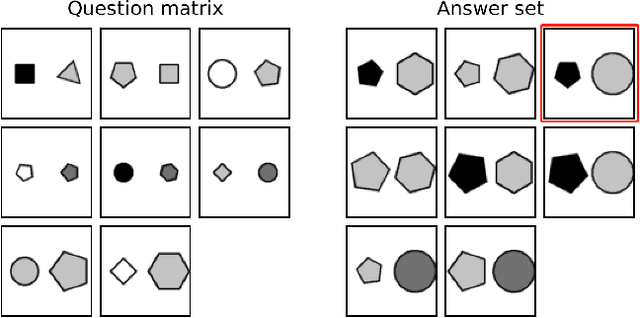
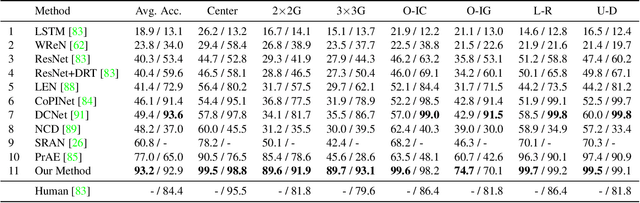
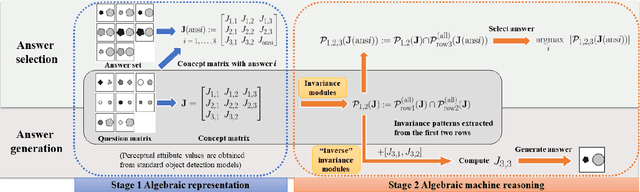
We introduce algebraic machine reasoning, a new reasoning framework that is well-suited for abstract reasoning. Effectively, algebraic machine reasoning reduces the difficult process of novel problem-solving to routine algebraic computation. The fundamental algebraic objects of interest are the ideals of some suitably initialized polynomial ring. We shall explain how solving Raven's Progressive Matrices (RPMs) can be realized as computational problems in algebra, which combine various well-known algebraic subroutines that include: Computing the Gr\"obner basis of an ideal, checking for ideal containment, etc. Crucially, the additional algebraic structure satisfied by ideals allows for more operations on ideals beyond set-theoretic operations. Our algebraic machine reasoning framework is not only able to select the correct answer from a given answer set, but also able to generate the correct answer with only the question matrix given. Experiments on the I-RAVEN dataset yield an overall $93.2\%$ accuracy, which significantly outperforms the current state-of-the-art accuracy of $77.0\%$ and exceeds human performance at $84.4\%$ accuracy.

FedCorr: Multi-Stage Federated Learning for Label Noise Correction

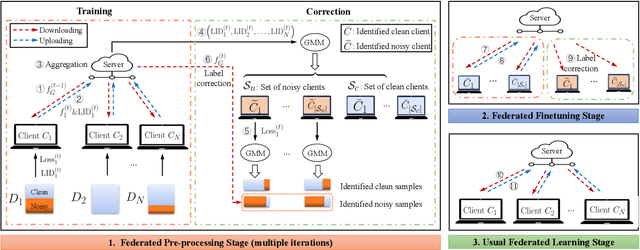
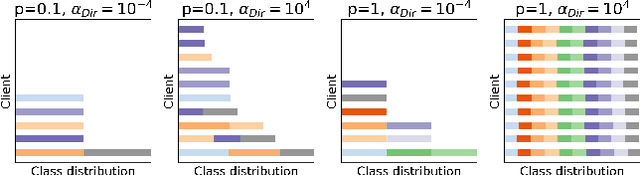
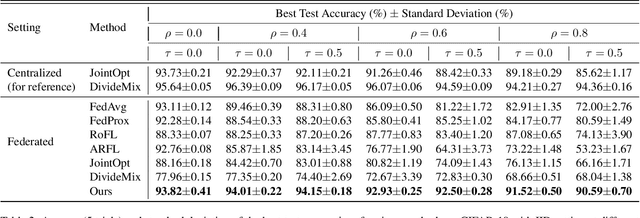
Federated learning (FL) is a privacy-preserving distributed learning paradigm that enables clients to jointly train a global model. In real-world FL implementations, client data could have label noise, and different clients could have vastly different label noise levels. Although there exist methods in centralized learning for tackling label noise, such methods do not perform well on heterogeneous label noise in FL settings, due to the typically smaller sizes of client datasets and data privacy requirements in FL. In this paper, we propose $\texttt{FedCorr}$, a general multi-stage framework to tackle heterogeneous label noise in FL, without making any assumptions on the noise models of local clients, while still maintaining client data privacy. In particular, (1) $\texttt{FedCorr}$ dynamically identifies noisy clients by exploiting the dimensionalities of the model prediction subspaces independently measured on all clients, and then identifies incorrect labels on noisy clients based on per-sample losses. To deal with data heterogeneity and to increase training stability, we propose an adaptive local proximal regularization term that is based on estimated local noise levels. (2) We further finetune the global model on identified clean clients and correct the noisy labels for the remaining noisy clients after finetuning. (3) Finally, we apply the usual training on all clients to make full use of all local data. Experiments conducted on CIFAR-10/100 with federated synthetic label noise, and on a real-world noisy dataset, Clothing1M, demonstrate that $\texttt{FedCorr}$ is robust to label noise and substantially outperforms the state-of-the-art methods at multiple noise levels.

Dynamic Attention-based Communication-Efficient Federated Learning

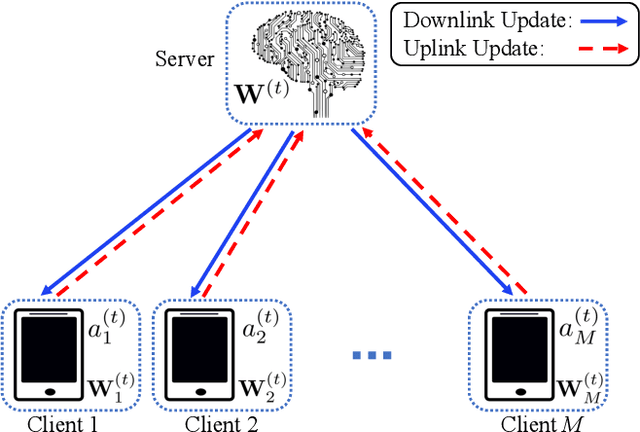
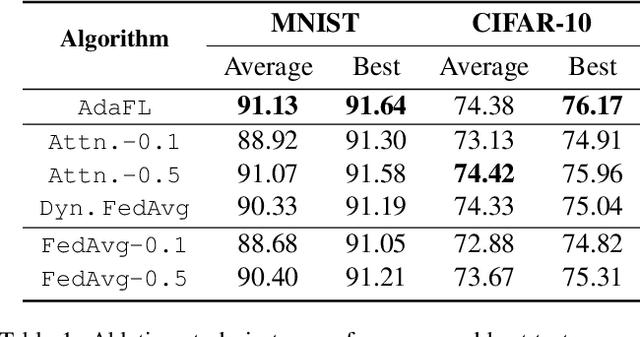
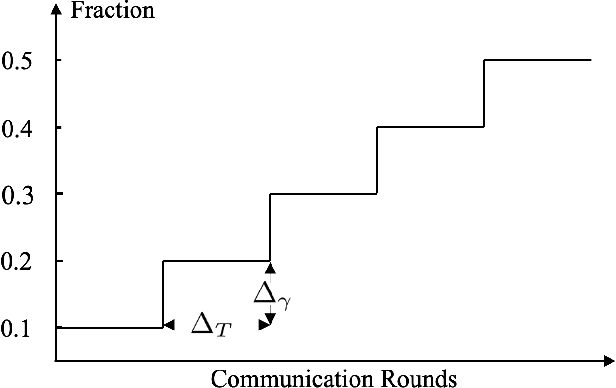
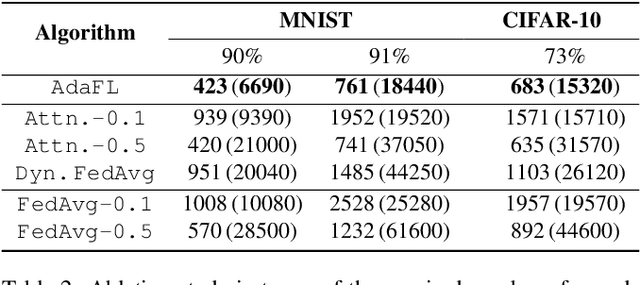
Federated learning (FL) offers a solution to train a global machine learning model while still maintaining data privacy, without needing access to data stored locally at the clients. However, FL suffers performance degradation when client data distribution is non-IID, and a longer training duration to combat this degradation may not necessarily be feasible due to communication limitations. To address this challenge, we propose a new adaptive training algorithm $\texttt{AdaFL}$, which comprises two components: (i) an attention-based client selection mechanism for a fairer training scheme among the clients; and (ii) a dynamic fraction method to balance the trade-off between performance stability and communication efficiency. Experimental results show that our $\texttt{AdaFL}$ algorithm outperforms the usual $\texttt{FedAvg}$ algorithm, and can be incorporated to further improve various state-of-the-art FL algorithms, with respect to three aspects: model accuracy, performance stability, and communication efficiency.

Training Classifiers that are Universally Robust to All Label Noise Levels

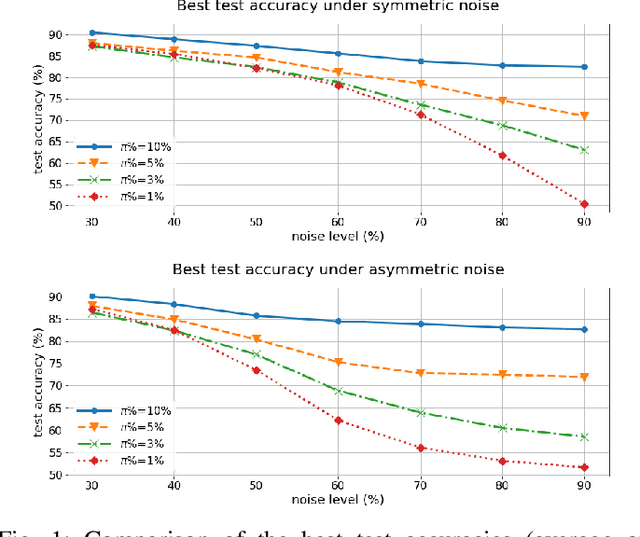
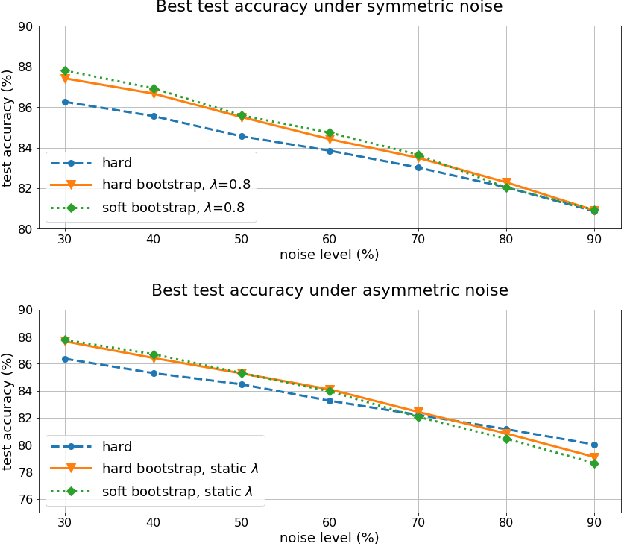
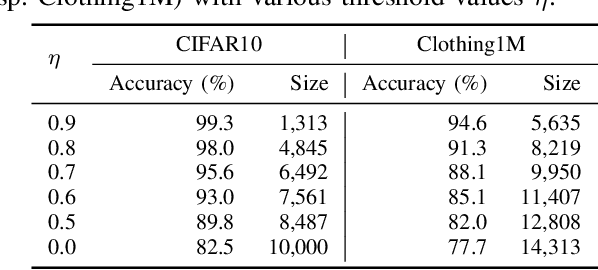
For classification tasks, deep neural networks are prone to overfitting in the presence of label noise. Although existing methods are able to alleviate this problem at low noise levels, they encounter significant performance reduction at high noise levels, or even at medium noise levels when the label noise is asymmetric. To train classifiers that are universally robust to all noise levels, and that are not sensitive to any variation in the noise model, we propose a distillation-based framework that incorporates a new subcategory of Positive-Unlabeled learning. In particular, we shall assume that a small subset of any given noisy dataset is known to have correct labels, which we treat as "positive", while the remaining noisy subset is treated as "unlabeled". Our framework consists of the following two components: (1) We shall generate, via iterative updates, an augmented clean subset with additional reliable "positive" samples filtered from "unlabeled" samples; (2) We shall train a teacher model on this larger augmented clean set. With the guidance of the teacher model, we then train a student model on the whole dataset. Experiments were conducted on the CIFAR-10 dataset with synthetic label noise at multiple noise levels for both symmetric and asymmetric noise. The results show that our framework generally outperforms at medium to high noise levels. We also evaluated our framework on Clothing1M, a real-world noisy dataset, and we achieved 2.94% improvement in accuracy over existing state-of-the-art methods.

A closer look at the approximation capabilities of neural networks

The universal approximation theorem, in one of its most general versions, says that if we consider only continuous activation functions $\sigma$, then a standard feedforward neural network with one hidden layer is able to approximate any continuous multivariate function $f$ to any given approximation threshold $\varepsilon$, if and only if $\sigma$ is non-polynomial. In this paper, we give a direct algebraic proof of the theorem. Furthermore we shall explicitly quantify the number of hidden units required for approximation. Specifically, if $X\subseteq \mathbb{R}^n$ is compact, then a neural network with $n$ input units, $m$ output units, and a single hidden layer with $\binom{n+d}{d}$ hidden units (independent of $m$ and $\varepsilon$), can uniformly approximate any polynomial function $f:X \to \mathbb{R}^m$ whose total degree is at most $d$ for each of its $m$ coordinate functions. In the general case that $f$ is any continuous function, we show there exists some $N\in \mathcal{O}(\varepsilon^{-n})$ (independent of $m$), such that $N$ hidden units would suffice to approximate $f$. We also show that this uniform approximation property (UAP) still holds even under seemingly strong conditions imposed on the weights. We highlight several consequences: (i) For any $\delta > 0$, the UAP still holds if we restrict all non-bias weights $w$ in the last layer to satisfy $|w| < \delta$. (ii) There exists some $\lambda>0$ (depending only on $f$ and $\sigma$), such that the UAP still holds if we restrict all non-bias weights $w$ in the first layer to satisfy $|w|>\lambda$. (iii) If the non-bias weights in the first layer are \emph{fixed} and randomly chosen from a suitable range, then the UAP holds with probability $1$.