Quantum Algorithms for the Pathwise Lasso

We present a novel quantum high-dimensional linear regression algorithm with an $\ell_1$-penalty based on the classical LARS (Least Angle Regression) pathwise algorithm. Similarly to available classical numerical algorithms for Lasso, our quantum algorithm provides the full regularisation path as the penalty term varies, but quadratically faster per iteration under specific conditions. A quadratic speedup on the number of features/predictors $d$ is possible by using the simple quantum minimum-finding subroutine from D\"urr and Hoyer (arXiv'96) in order to obtain the joining time at each iteration. We then improve upon this simple quantum algorithm and obtain a quadratic speedup both in the number of features $d$ and the number of observations $n$ by using the recent approximate quantum minimum-finding subroutine from Chen and de Wolf (ICALP'23). As one of our main contributions, we construct a quantum unitary based on quantum amplitude estimation to approximately compute the joining times to be searched over by the approximate quantum minimum finding. Since the joining times are no longer exactly computed, it is no longer clear that the resulting approximate quantum algorithm obtains a good solution. As our second main contribution, we prove, via an approximate version of the KKT conditions and a duality gap, that the LARS algorithm (and therefore our quantum algorithm) is robust to errors. This means that it still outputs a path that minimises the Lasso cost function up to a small error if the joining times are only approximately computed. Finally, in the model where the observations are generated by an underlying linear model with an unknown coefficient vector, we prove bounds on the difference between the unknown coefficient vector and the approximate Lasso solution, which generalises known results about convergence rates in classical statistical learning theory analysis.

Adapter Pruning using Tropical Characterization

Adapters are widely popular parameter-efficient transfer learning approaches in natural language processing that insert trainable modules in between layers of a pre-trained language model. Apart from several heuristics, however, there has been a lack of studies analyzing the optimal number of adapter parameters needed for downstream applications. In this paper, we propose an adapter pruning approach by studying the tropical characteristics of trainable modules. We cast it as an optimization problem that aims to prune parameters from the adapter layers without changing the orientation of underlying tropical hypersurfaces. Our experiments on five NLP datasets show that tropical geometry tends to identify more relevant parameters to prune when compared with the magnitude-based baseline, while a combined approach works best across the tasks.

Abstract Visual Reasoning: An Algebraic Approach for Solving Raven's Progressive Matrices

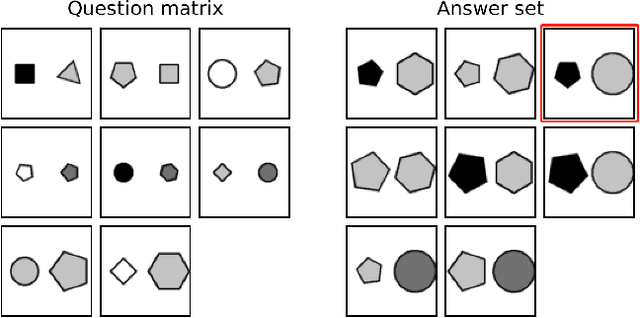
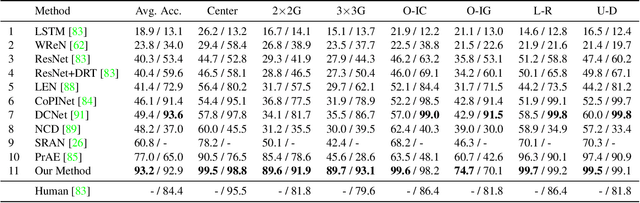
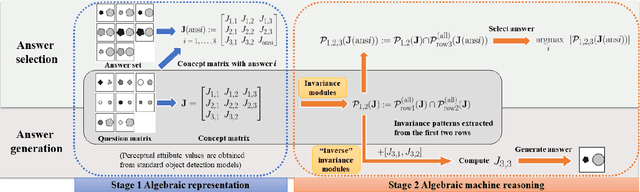
We introduce algebraic machine reasoning, a new reasoning framework that is well-suited for abstract reasoning. Effectively, algebraic machine reasoning reduces the difficult process of novel problem-solving to routine algebraic computation. The fundamental algebraic objects of interest are the ideals of some suitably initialized polynomial ring. We shall explain how solving Raven's Progressive Matrices (RPMs) can be realized as computational problems in algebra, which combine various well-known algebraic subroutines that include: Computing the Gr\"obner basis of an ideal, checking for ideal containment, etc. Crucially, the additional algebraic structure satisfied by ideals allows for more operations on ideals beyond set-theoretic operations. Our algebraic machine reasoning framework is not only able to select the correct answer from a given answer set, but also able to generate the correct answer with only the question matrix given. Experiments on the I-RAVEN dataset yield an overall $93.2\%$ accuracy, which significantly outperforms the current state-of-the-art accuracy of $77.0\%$ and exceeds human performance at $84.4\%$ accuracy.

Federated Distillation of Natural Language Understanding with Confident Sinkhorns

Enhancing the user experience is an essential task for application service providers. For instance, two users living wide apart may have different tastes of food. A food recommender mobile application installed on an edge device might want to learn from user feedback (reviews) to satisfy the client's needs pertaining to distinct domains. Retrieving user data comes at the cost of privacy while asking for model parameters trained on a user device becomes space inefficient at a large scale. In this work, we propose an approach to learn a central (global) model from the federation of (local) models which are trained on user-devices, without disclosing the local data or model parameters to the server. We propose a federation mechanism for the problems with natural similarity metric between the labels which commonly appear in natural language understanding (NLU) tasks. To learn the global model, the objective is to minimize the optimal transport cost of the global model's predictions from the confident sum of soft-targets assigned by local models. The confidence (a model weighting scheme) score of a model is defined as the L2 distance of a model's prediction from its probability bias. The method improves the global model's performance over the baseline designed on three NLU tasks with intrinsic label space semantics, i.e., fine-grained sentiment analysis, emotion recognition in conversation, and natural language inference. We make our codes public at https://github.com/declare-lab/sinkhorn-loss.

Topological Mapping for Manhattan-like Repetitive Environments

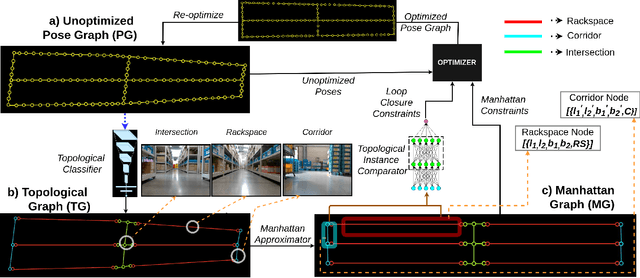
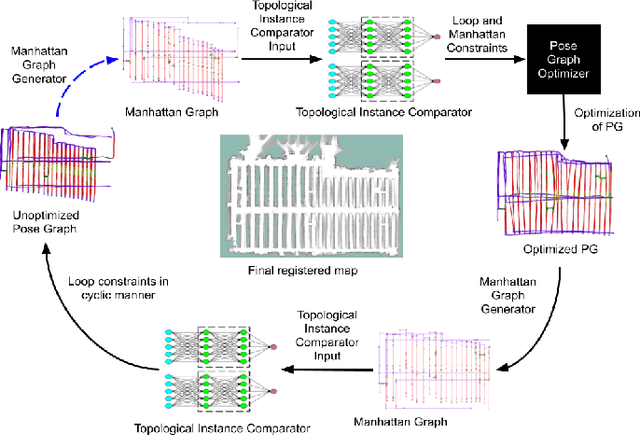
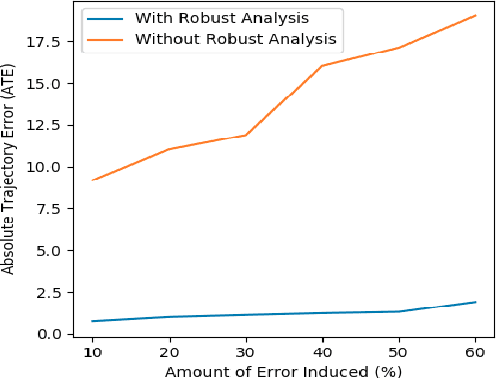
We showcase a topological mapping framework for a challenging indoor warehouse setting. At the most abstract level, the warehouse is represented as a Topological Graph where the nodes of the graph represent a particular warehouse topological construct (e.g. rackspace, corridor) and the edges denote the existence of a path between two neighbouring nodes or topologies. At the intermediate level, the map is represented as a Manhattan Graph where the nodes and edges are characterized by Manhattan properties and as a Pose Graph at the lower-most level of detail. The topological constructs are learned via a Deep Convolutional Network while the relational properties between topological instances are learnt via a Siamese-style Neural Network. In the paper, we show that maintaining abstractions such as Topological Graph and Manhattan Graph help in recovering an accurate Pose Graph starting from a highly erroneous and unoptimized Pose Graph. We show how this is achieved by embedding topological and Manhattan relations as well as Manhattan Graph aided loop closure relations as constraints in the backend Pose Graph optimization framework. The recovery of near ground-truth Pose Graph on real-world indoor warehouse scenes vindicate the efficacy of the proposed framework.

Learning Agents in Black-Scholes Financial Markets: Consensus Dynamics and Volatility Smiles

Black-Scholes (BS) is the standard mathematical model for option pricing in financial markets. Option prices are calculated using an analytical formula whose main inputs are strike (at which price to exercise) and volatility. The BS framework assumes that volatility remains constant across all strikes, however, in practice it varies. How do traders come to learn these parameters? We introduce natural models of learning agents, in which they update their beliefs about the true implied volatility based on the opinions of other traders. We prove convergence of these opinion dynamics using techniques from control theory and leader-follower models, thus providing a resolution between theory and market practices. We allow for two different models, one with feedback and one with an unknown leader.