Quantum Algorithms for the Pathwise Lasso

We present a novel quantum high-dimensional linear regression algorithm with an $\ell_1$-penalty based on the classical LARS (Least Angle Regression) pathwise algorithm. Similarly to available classical numerical algorithms for Lasso, our quantum algorithm provides the full regularisation path as the penalty term varies, but quadratically faster per iteration under specific conditions. A quadratic speedup on the number of features/predictors $d$ is possible by using the simple quantum minimum-finding subroutine from D\"urr and Hoyer (arXiv'96) in order to obtain the joining time at each iteration. We then improve upon this simple quantum algorithm and obtain a quadratic speedup both in the number of features $d$ and the number of observations $n$ by using the recent approximate quantum minimum-finding subroutine from Chen and de Wolf (ICALP'23). As one of our main contributions, we construct a quantum unitary based on quantum amplitude estimation to approximately compute the joining times to be searched over by the approximate quantum minimum finding. Since the joining times are no longer exactly computed, it is no longer clear that the resulting approximate quantum algorithm obtains a good solution. As our second main contribution, we prove, via an approximate version of the KKT conditions and a duality gap, that the LARS algorithm (and therefore our quantum algorithm) is robust to errors. This means that it still outputs a path that minimises the Lasso cost function up to a small error if the joining times are only approximately computed. Finally, in the model where the observations are generated by an underlying linear model with an unknown coefficient vector, we prove bounds on the difference between the unknown coefficient vector and the approximate Lasso solution, which generalises known results about convergence rates in classical statistical learning theory analysis.

A Subgame Perfect Equilibrium Reinforcement Learning Approach to Time-inconsistent Problems

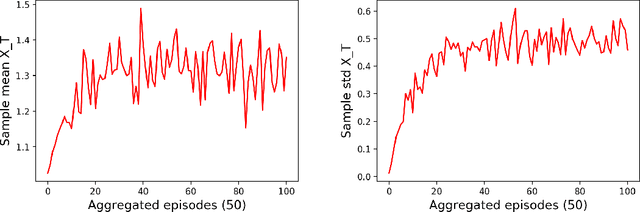
In this paper, we establish a subgame perfect equilibrium reinforcement learning (SPERL) framework for time-inconsistent (TIC) problems. In the context of RL, TIC problems are known to face two main challenges: the non-existence of natural recursive relationships between value functions at different time points and the violation of Bellman's principle of optimality that raises questions on the applicability of standard policy iteration algorithms for unprovable policy improvement theorems. We adapt an extended dynamic programming theory and propose a new class of algorithms, called backward policy iteration (BPI), that solves SPERL and addresses both challenges. To demonstrate the practical usage of BPI as a training framework, we adapt standard RL simulation methods and derive two BPI-based training algorithms. We examine our derived training frameworks on a mean-variance portfolio selection problem and evaluate some performance metrics including convergence and model identifiability.