Quaternion recurrent neural network with real-time recurrent learning and maximum correntropy criterion

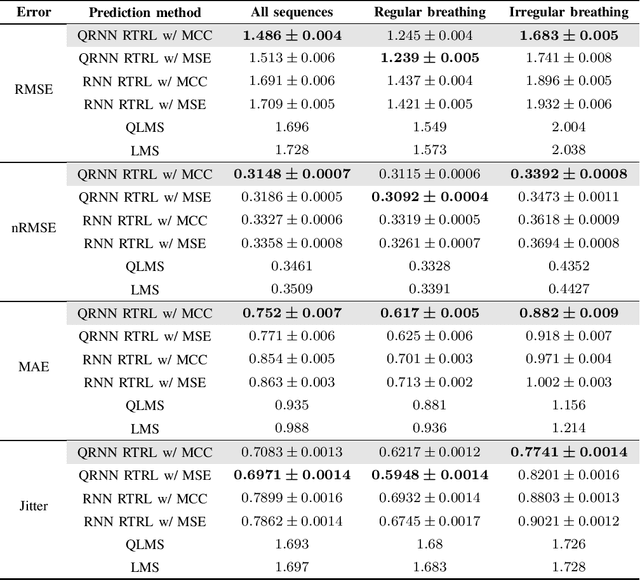
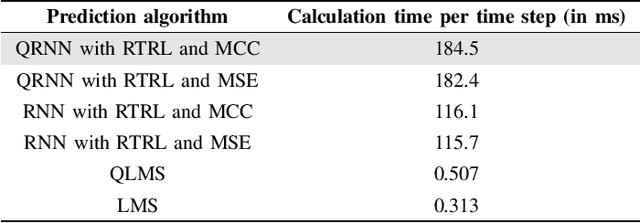
We develop a robust quaternion recurrent neural network (QRNN) for real-time processing of 3D and 4D data with outliers. This is achieved by combining the real-time recurrent learning (RTRL) algorithm and the maximum correntropy criterion (MCC) as a loss function. While both the mean square error and maximum correntropy criterion are viable cost functions, it is shown that the non-quadratic maximum correntropy loss function is less sensitive to outliers, making it suitable for applications with multidimensional noisy or uncertain data. Both algorithms are derived based on the novel generalised HR (GHR) calculus, which allows for the differentiation of real functions of quaternion variables and offers the product and chain rules, thus enabling elegant and compact derivations. Simulation results in the context of motion prediction of chest internal markers for lung cancer radiotherapy, which includes regular and irregular breathing sequences, support the analysis.

The HR-Calculus: Enabling Information Processing with Quaternion Algebra

From their inception, quaternions and their division algebra have proven to be advantageous in modelling rotation/orientation in three-dimensional spaces and have seen use from the initial formulation of electromagnetic filed theory through to forming the basis of quantum filed theory. Despite their impressive versatility in modelling real-world phenomena, adaptive information processing techniques specifically designed for quaternion-valued signals have only recently come to the attention of the machine learning, signal processing, and control communities. The most important development in this direction is introduction of the HR-calculus, which provides the required mathematical foundation for deriving adaptive information processing techniques directly in the quaternion domain. In this article, the foundations of the HR-calculus are revised and the required tools for deriving adaptive learning techniques suitable for dealing with quaternion-valued signals, such as the gradient operator, chain and product derivative rules, and Taylor series expansion are presented. This serves to establish the most important applications of adaptive information processing in the quaternion domain for both single-node and multi-node formulations. The article is supported by Supplementary Material, which will be referred to as SM.

Convergence of Adam for Non-convex Objectives: Relaxed Hyperparameters and Non-ergodic Case

Adam is a commonly used stochastic optimization algorithm in machine learning. However, its convergence is still not fully understood, especially in the non-convex setting. This paper focuses on exploring hyperparameter settings for the convergence of vanilla Adam and tackling the challenges of non-ergodic convergence related to practical application. The primary contributions are summarized as follows: firstly, we introduce precise definitions of ergodic and non-ergodic convergence, which cover nearly all forms of convergence for stochastic optimization algorithms. Meanwhile, we emphasize the superiority of non-ergodic convergence over ergodic convergence. Secondly, we establish a weaker sufficient condition for the ergodic convergence guarantee of Adam, allowing a more relaxed choice of hyperparameters. On this basis, we achieve the almost sure ergodic convergence rate of Adam, which is arbitrarily close to $o(1/\sqrt{K})$. More importantly, we prove, for the first time, that the last iterate of Adam converges to a stationary point for non-convex objectives. Finally, we obtain the non-ergodic convergence rate of $O(1/K)$ for function values under the Polyak-Lojasiewicz (PL) condition. These findings build a solid theoretical foundation for Adam to solve non-convex stochastic optimization problems.

Convex Quaternion Optimization for Signal Processing: Theory and Applications

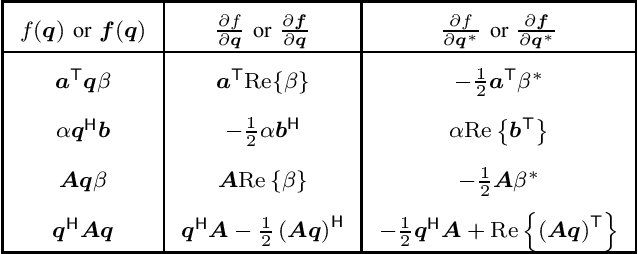
Convex optimization methods have been extensively used in the fields of communications and signal processing. However, the theory of quaternion optimization is currently not as fully developed and systematic as that of complex and real optimization. To this end, we establish an essential theory of convex quaternion optimization for signal processing based on the generalized Hamilton-real (GHR) calculus. This is achieved in a way which conforms with traditional complex and real optimization theory. For rigorous, We present five discriminant theorems for convex quaternion functions, and four discriminant criteria for strongly convex quaternion functions. Furthermore, we provide a fundamental theorem for the optimality of convex quaternion optimization problems, and demonstrate its utility through three applications in quaternion signal processing. These results provide a solid theoretical foundation for convex quaternion optimization and open avenues for further developments in signal processing applications.

UAdam: Unified Adam-Type Algorithmic Framework for Non-Convex Stochastic Optimization

Adam-type algorithms have become a preferred choice for optimisation in the deep learning setting, however, despite success, their convergence is still not well understood. To this end, we introduce a unified framework for Adam-type algorithms (called UAdam). This is equipped with a general form of the second-order moment, which makes it possible to include Adam and its variants as special cases, such as NAdam, AMSGrad, AdaBound, AdaFom, and Adan. This is supported by a rigorous convergence analysis of UAdam in the non-convex stochastic setting, showing that UAdam converges to the neighborhood of stationary points with the rate of $\mathcal{O}(1/T)$. Furthermore, the size of neighborhood decreases as $\beta$ increases. Importantly, our analysis only requires the first-order momentum factor to be close enough to 1, without any restrictions on the second-order momentum factor. Theoretical results also show that vanilla Adam can converge by selecting appropriate hyperparameters, which provides a theoretical guarantee for the analysis, applications, and further developments of the whole class of Adam-type algorithms.

Last-iterate convergence analysis of stochastic momentum methods for neural networks

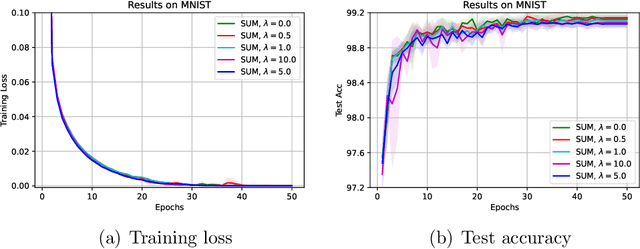
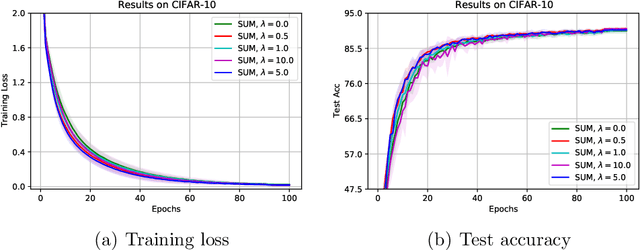
The stochastic momentum method is a commonly used acceleration technique for solving large-scale stochastic optimization problems in artificial neural networks. Current convergence results of stochastic momentum methods under non-convex stochastic settings mostly discuss convergence in terms of the random output and minimum output. To this end, we address the convergence of the last iterate output (called last-iterate convergence) of the stochastic momentum methods for non-convex stochastic optimization problems, in a way conformal with traditional optimization theory. We prove the last-iterate convergence of the stochastic momentum methods under a unified framework, covering both stochastic heavy ball momentum and stochastic Nesterov accelerated gradient momentum. The momentum factors can be fixed to be constant, rather than time-varying coefficients in existing analyses. Finally, the last-iterate convergence of the stochastic momentum methods is verified on the benchmark MNIST and CIFAR-10 datasets.

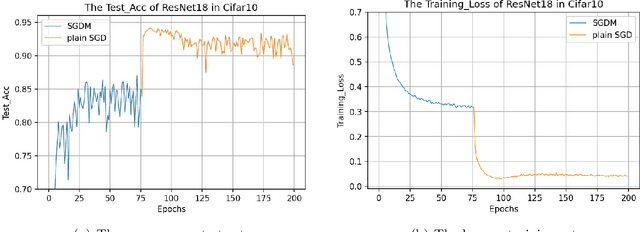
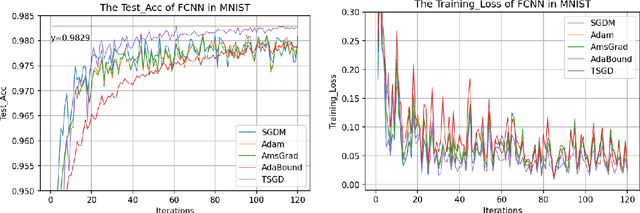
Scaling transition from momentum stochastic gradient descent to plain stochastic gradient descent

The plain stochastic gradient descent and momentum stochastic gradient descent have extremely wide applications in deep learning due to their simple settings and low computational complexity. The momentum stochastic gradient descent uses the accumulated gradient as the updated direction of the current parameters, which has a faster training speed. Because the direction of the plain stochastic gradient descent has not been corrected by the accumulated gradient. For the parameters that currently need to be updated, it is the optimal direction, and its update is more accurate. We combine the advantages of the momentum stochastic gradient descent with fast training speed and the plain stochastic gradient descent with high accuracy, and propose a scaling transition from momentum stochastic gradient descent to plain stochastic gradient descent(TSGD) method. At the same time, a learning rate that decreases linearly with the iterations is used instead of a constant learning rate. The TSGD algorithm has a larger step size in the early stage to speed up the training, and training with a smaller step size in the later stage can steadily converge. Our experimental results show that the TSGD algorithm has faster training speed, higher accuracy and better stability. Our implementation is available at: https://github.com/kunzeng/TSGD.

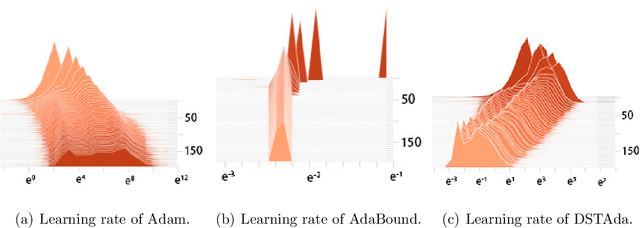
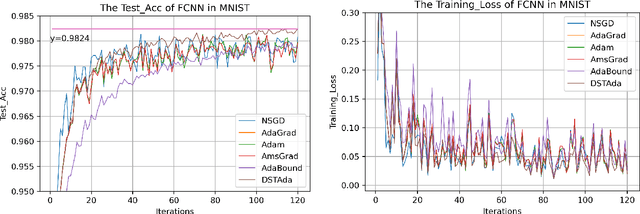
Decreasing scaling transition from adaptive gradient descent to stochastic gradient descent

Currently, researchers have proposed the adaptive gradient descent algorithm and its variants, such as AdaGrad, RMSProp, Adam, AmsGrad, etc. Although these algorithms have a faster speed in the early stage, the generalization ability in the later stage of training is often not as good as the stochastic gradient descent. Recently, some researchers have combined the adaptive gradient descent and stochastic gradient descent to obtain the advantages of both and achieved good results. Based on this research, we propose a decreasing scaling transition from adaptive gradient descent to stochastic gradient descent method(DSTAda). For the training stage of the stochastic gradient descent, we use a learning rate that decreases linearly with the number of iterations instead of a constant learning rate. We achieve a smooth and stable transition from adaptive gradient descent to stochastic gradient descent through scaling. At the same time, we give a theoretical proof of the convergence of DSTAda under the framework of online learning. Our experimental results show that the DSTAda algorithm has a faster convergence speed, higher accuracy, and better stability and robustness. Our implementation is available at: https://github.com/kunzeng/DSTAdam.

Quaternion Gradient and Hessian

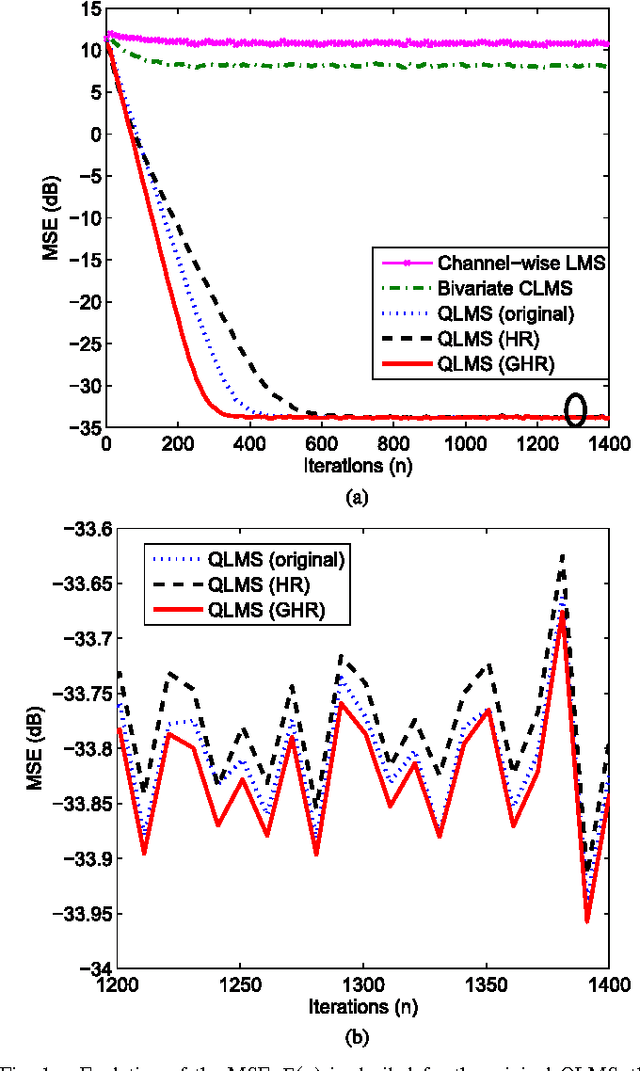
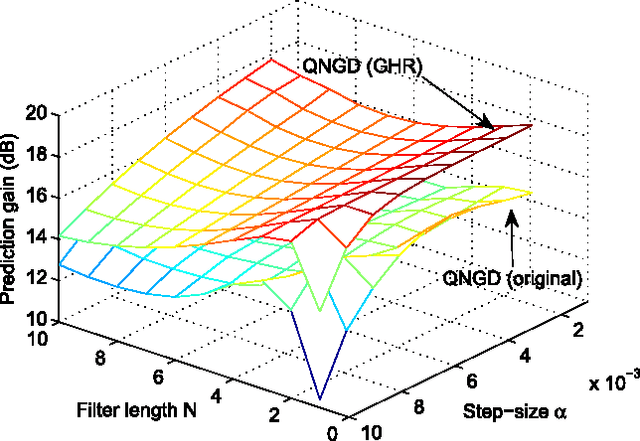
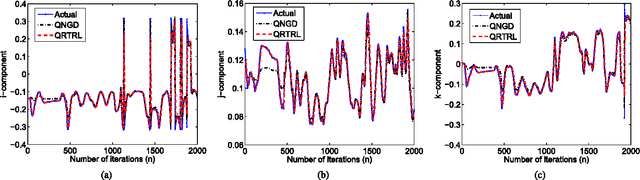
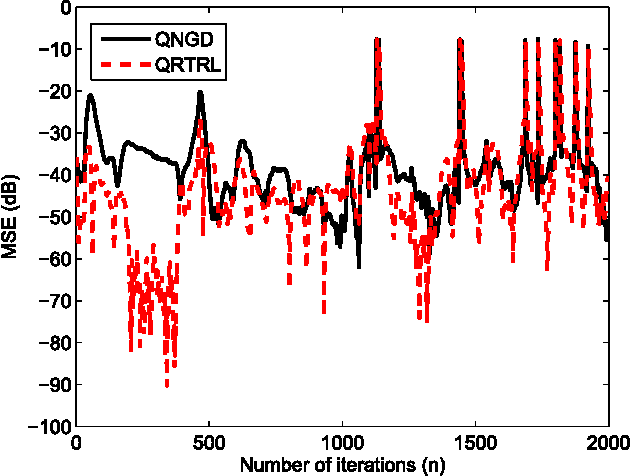
The optimization of real scalar functions of quaternion variables, such as the mean square error or array output power, underpins many practical applications. Solutions often require the calculation of the gradient and Hessian, however, real functions of quaternion variables are essentially non-analytic. To address this issue, we propose new definitions of quaternion gradient and Hessian, based on the novel generalized HR (GHR) calculus, thus making possible efficient derivation of optimization algorithms directly in the quaternion field, rather than transforming the problem to the real domain, as is current practice. In addition, unlike the existing quaternion gradients, the GHR calculus allows for the product and chain rule, and for a one-to-one correspondence of the proposed quaternion gradient and Hessian with their real counterparts. Properties of the quaternion gradient and Hessian relevant to numerical applications are elaborated, and the results illuminate the usefulness of the GHR calculus in greatly simplifying the derivation of the quaternion least mean squares, and in quaternion least square and Newton algorithm. The proposed gradient and Hessian are also shown to enable the same generic forms as the corresponding real- and complex-valued algorithms, further illustrating the advantages in algorithm design and evaluation.