Last-iterate convergence analysis of stochastic momentum methods for neural networks
Paper and Code
May 30, 2022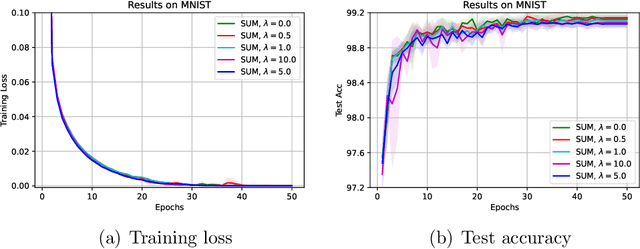
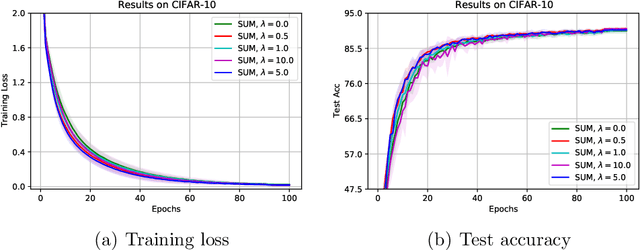
The stochastic momentum method is a commonly used acceleration technique for solving large-scale stochastic optimization problems in artificial neural networks. Current convergence results of stochastic momentum methods under non-convex stochastic settings mostly discuss convergence in terms of the random output and minimum output. To this end, we address the convergence of the last iterate output (called last-iterate convergence) of the stochastic momentum methods for non-convex stochastic optimization problems, in a way conformal with traditional optimization theory. We prove the last-iterate convergence of the stochastic momentum methods under a unified framework, covering both stochastic heavy ball momentum and stochastic Nesterov accelerated gradient momentum. The momentum factors can be fixed to be constant, rather than time-varying coefficients in existing analyses. Finally, the last-iterate convergence of the stochastic momentum methods is verified on the benchmark MNIST and CIFAR-10 datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge