Convergence of Adam for Non-convex Objectives: Relaxed Hyperparameters and Non-ergodic Case

Adam is a commonly used stochastic optimization algorithm in machine learning. However, its convergence is still not fully understood, especially in the non-convex setting. This paper focuses on exploring hyperparameter settings for the convergence of vanilla Adam and tackling the challenges of non-ergodic convergence related to practical application. The primary contributions are summarized as follows: firstly, we introduce precise definitions of ergodic and non-ergodic convergence, which cover nearly all forms of convergence for stochastic optimization algorithms. Meanwhile, we emphasize the superiority of non-ergodic convergence over ergodic convergence. Secondly, we establish a weaker sufficient condition for the ergodic convergence guarantee of Adam, allowing a more relaxed choice of hyperparameters. On this basis, we achieve the almost sure ergodic convergence rate of Adam, which is arbitrarily close to $o(1/\sqrt{K})$. More importantly, we prove, for the first time, that the last iterate of Adam converges to a stationary point for non-convex objectives. Finally, we obtain the non-ergodic convergence rate of $O(1/K)$ for function values under the Polyak-Lojasiewicz (PL) condition. These findings build a solid theoretical foundation for Adam to solve non-convex stochastic optimization problems.

UAdam: Unified Adam-Type Algorithmic Framework for Non-Convex Stochastic Optimization

Adam-type algorithms have become a preferred choice for optimisation in the deep learning setting, however, despite success, their convergence is still not well understood. To this end, we introduce a unified framework for Adam-type algorithms (called UAdam). This is equipped with a general form of the second-order moment, which makes it possible to include Adam and its variants as special cases, such as NAdam, AMSGrad, AdaBound, AdaFom, and Adan. This is supported by a rigorous convergence analysis of UAdam in the non-convex stochastic setting, showing that UAdam converges to the neighborhood of stationary points with the rate of $\mathcal{O}(1/T)$. Furthermore, the size of neighborhood decreases as $\beta$ increases. Importantly, our analysis only requires the first-order momentum factor to be close enough to 1, without any restrictions on the second-order momentum factor. Theoretical results also show that vanilla Adam can converge by selecting appropriate hyperparameters, which provides a theoretical guarantee for the analysis, applications, and further developments of the whole class of Adam-type algorithms.

Last-iterate convergence analysis of stochastic momentum methods for neural networks

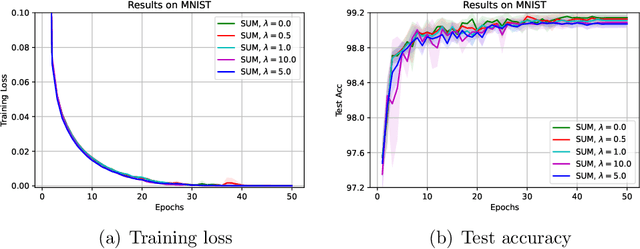
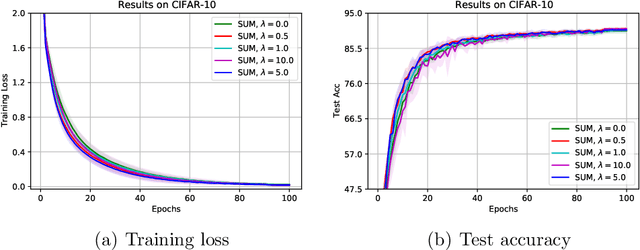
The stochastic momentum method is a commonly used acceleration technique for solving large-scale stochastic optimization problems in artificial neural networks. Current convergence results of stochastic momentum methods under non-convex stochastic settings mostly discuss convergence in terms of the random output and minimum output. To this end, we address the convergence of the last iterate output (called last-iterate convergence) of the stochastic momentum methods for non-convex stochastic optimization problems, in a way conformal with traditional optimization theory. We prove the last-iterate convergence of the stochastic momentum methods under a unified framework, covering both stochastic heavy ball momentum and stochastic Nesterov accelerated gradient momentum. The momentum factors can be fixed to be constant, rather than time-varying coefficients in existing analyses. Finally, the last-iterate convergence of the stochastic momentum methods is verified on the benchmark MNIST and CIFAR-10 datasets.

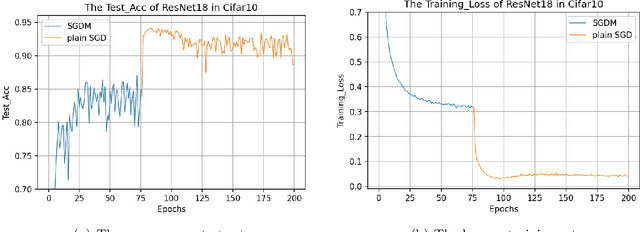
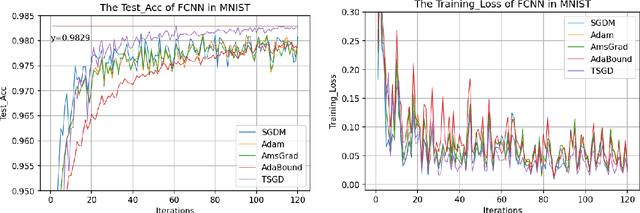
Scaling transition from momentum stochastic gradient descent to plain stochastic gradient descent

The plain stochastic gradient descent and momentum stochastic gradient descent have extremely wide applications in deep learning due to their simple settings and low computational complexity. The momentum stochastic gradient descent uses the accumulated gradient as the updated direction of the current parameters, which has a faster training speed. Because the direction of the plain stochastic gradient descent has not been corrected by the accumulated gradient. For the parameters that currently need to be updated, it is the optimal direction, and its update is more accurate. We combine the advantages of the momentum stochastic gradient descent with fast training speed and the plain stochastic gradient descent with high accuracy, and propose a scaling transition from momentum stochastic gradient descent to plain stochastic gradient descent(TSGD) method. At the same time, a learning rate that decreases linearly with the iterations is used instead of a constant learning rate. The TSGD algorithm has a larger step size in the early stage to speed up the training, and training with a smaller step size in the later stage can steadily converge. Our experimental results show that the TSGD algorithm has faster training speed, higher accuracy and better stability. Our implementation is available at: https://github.com/kunzeng/TSGD.

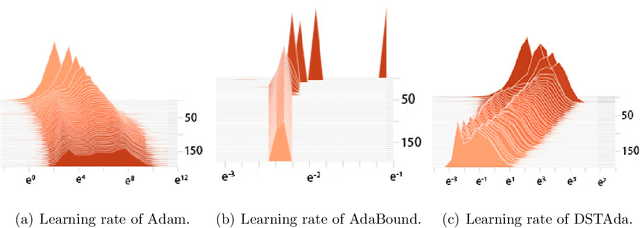
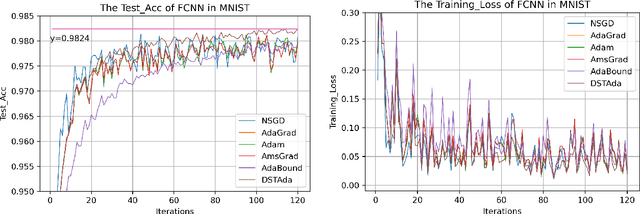
Decreasing scaling transition from adaptive gradient descent to stochastic gradient descent

Currently, researchers have proposed the adaptive gradient descent algorithm and its variants, such as AdaGrad, RMSProp, Adam, AmsGrad, etc. Although these algorithms have a faster speed in the early stage, the generalization ability in the later stage of training is often not as good as the stochastic gradient descent. Recently, some researchers have combined the adaptive gradient descent and stochastic gradient descent to obtain the advantages of both and achieved good results. Based on this research, we propose a decreasing scaling transition from adaptive gradient descent to stochastic gradient descent method(DSTAda). For the training stage of the stochastic gradient descent, we use a learning rate that decreases linearly with the number of iterations instead of a constant learning rate. We achieve a smooth and stable transition from adaptive gradient descent to stochastic gradient descent through scaling. At the same time, we give a theoretical proof of the convergence of DSTAda under the framework of online learning. Our experimental results show that the DSTAda algorithm has a faster convergence speed, higher accuracy, and better stability and robustness. Our implementation is available at: https://github.com/kunzeng/DSTAdam.