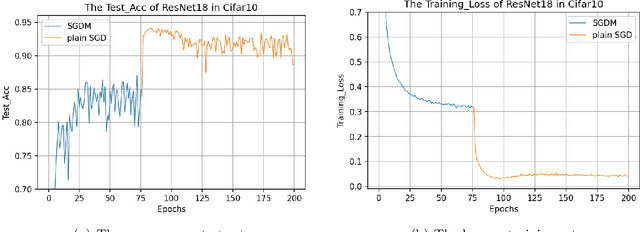
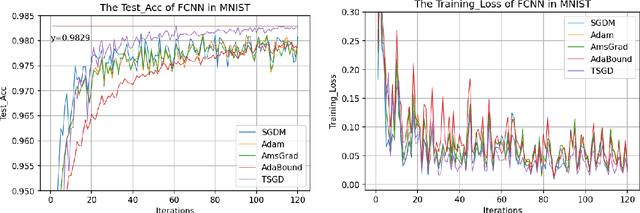
Scaling transition from momentum stochastic gradient descent to plain stochastic gradient descent

The plain stochastic gradient descent and momentum stochastic gradient descent have extremely wide applications in deep learning due to their simple settings and low computational complexity. The momentum stochastic gradient descent uses the accumulated gradient as the updated direction of the current parameters, which has a faster training speed. Because the direction of the plain stochastic gradient descent has not been corrected by the accumulated gradient. For the parameters that currently need to be updated, it is the optimal direction, and its update is more accurate. We combine the advantages of the momentum stochastic gradient descent with fast training speed and the plain stochastic gradient descent with high accuracy, and propose a scaling transition from momentum stochastic gradient descent to plain stochastic gradient descent(TSGD) method. At the same time, a learning rate that decreases linearly with the iterations is used instead of a constant learning rate. The TSGD algorithm has a larger step size in the early stage to speed up the training, and training with a smaller step size in the later stage can steadily converge. Our experimental results show that the TSGD algorithm has faster training speed, higher accuracy and better stability. Our implementation is available at: https://github.com/kunzeng/TSGD.

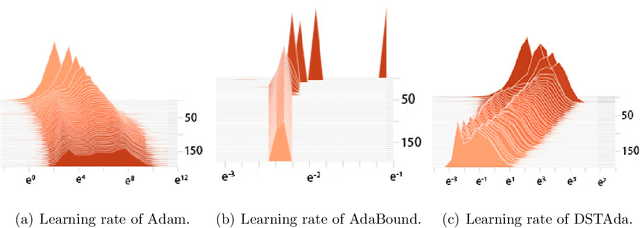
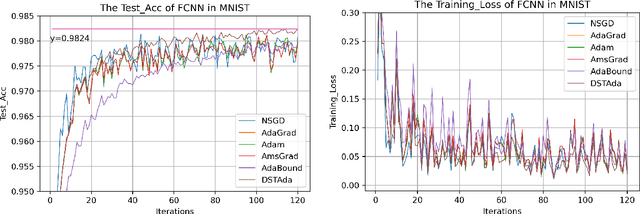
Decreasing scaling transition from adaptive gradient descent to stochastic gradient descent

Currently, researchers have proposed the adaptive gradient descent algorithm and its variants, such as AdaGrad, RMSProp, Adam, AmsGrad, etc. Although these algorithms have a faster speed in the early stage, the generalization ability in the later stage of training is often not as good as the stochastic gradient descent. Recently, some researchers have combined the adaptive gradient descent and stochastic gradient descent to obtain the advantages of both and achieved good results. Based on this research, we propose a decreasing scaling transition from adaptive gradient descent to stochastic gradient descent method(DSTAda). For the training stage of the stochastic gradient descent, we use a learning rate that decreases linearly with the number of iterations instead of a constant learning rate. We achieve a smooth and stable transition from adaptive gradient descent to stochastic gradient descent through scaling. At the same time, we give a theoretical proof of the convergence of DSTAda under the framework of online learning. Our experimental results show that the DSTAda algorithm has a faster convergence speed, higher accuracy, and better stability and robustness. Our implementation is available at: https://github.com/kunzeng/DSTAdam.