Quaternion Gradient and Hessian
Paper and Code
Jun 13, 2014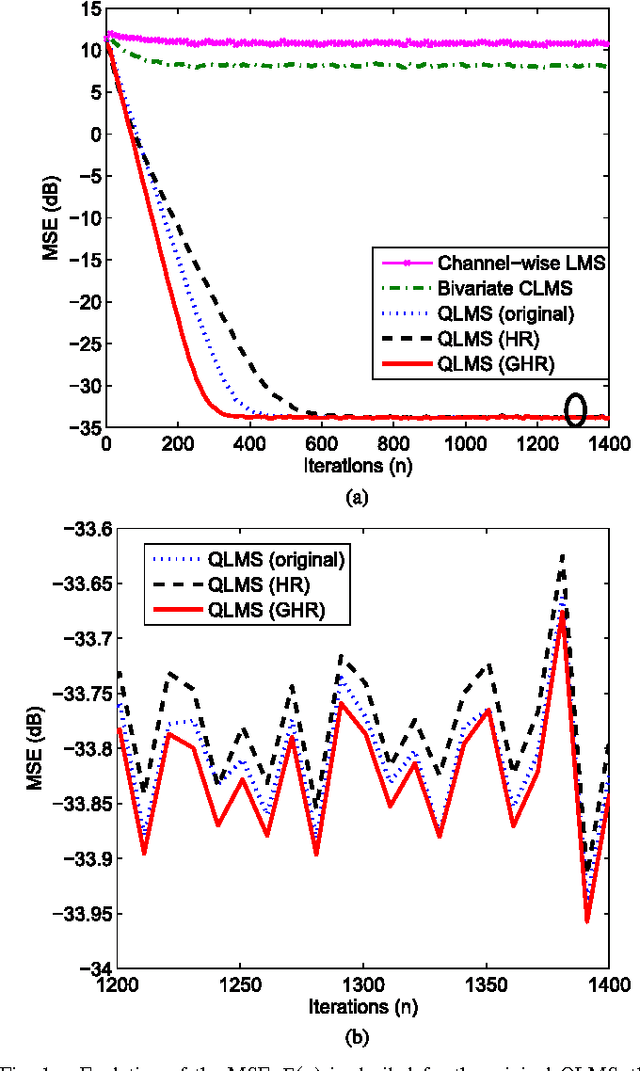
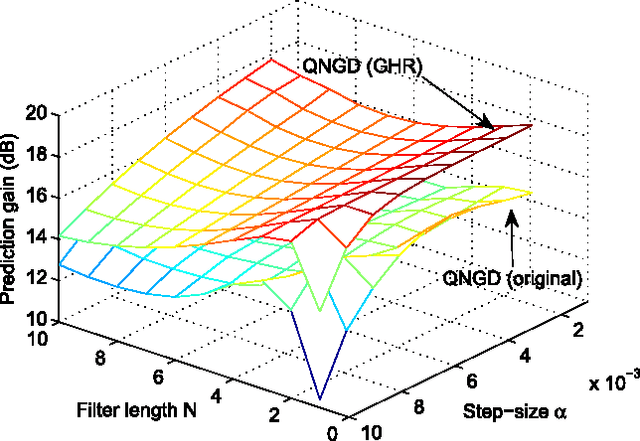
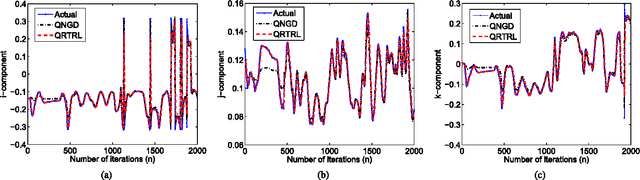
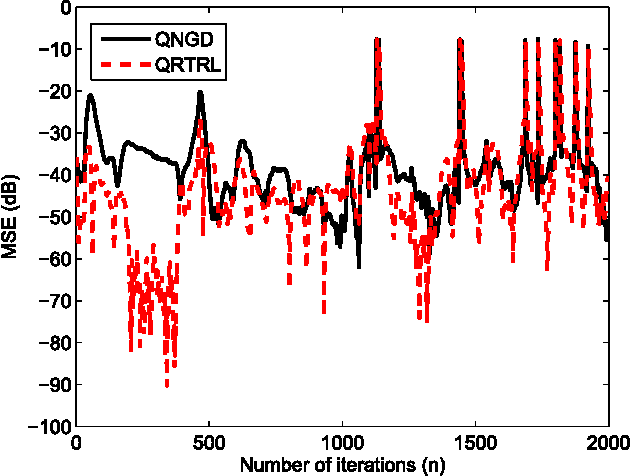
The optimization of real scalar functions of quaternion variables, such as the mean square error or array output power, underpins many practical applications. Solutions often require the calculation of the gradient and Hessian, however, real functions of quaternion variables are essentially non-analytic. To address this issue, we propose new definitions of quaternion gradient and Hessian, based on the novel generalized HR (GHR) calculus, thus making possible efficient derivation of optimization algorithms directly in the quaternion field, rather than transforming the problem to the real domain, as is current practice. In addition, unlike the existing quaternion gradients, the GHR calculus allows for the product and chain rule, and for a one-to-one correspondence of the proposed quaternion gradient and Hessian with their real counterparts. Properties of the quaternion gradient and Hessian relevant to numerical applications are elaborated, and the results illuminate the usefulness of the GHR calculus in greatly simplifying the derivation of the quaternion least mean squares, and in quaternion least square and Newton algorithm. The proposed gradient and Hessian are also shown to enable the same generic forms as the corresponding real- and complex-valued algorithms, further illustrating the advantages in algorithm design and evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge