Convex Quaternion Optimization for Signal Processing: Theory and Applications
Paper and Code
May 09, 2023
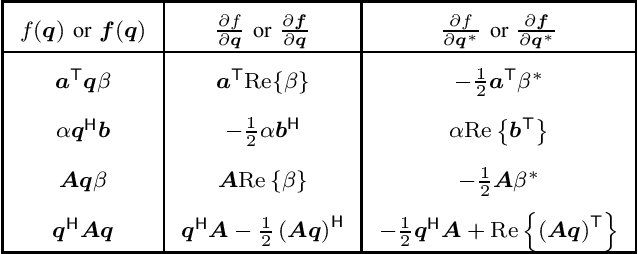
Convex optimization methods have been extensively used in the fields of communications and signal processing. However, the theory of quaternion optimization is currently not as fully developed and systematic as that of complex and real optimization. To this end, we establish an essential theory of convex quaternion optimization for signal processing based on the generalized Hamilton-real (GHR) calculus. This is achieved in a way which conforms with traditional complex and real optimization theory. For rigorous, We present five discriminant theorems for convex quaternion functions, and four discriminant criteria for strongly convex quaternion functions. Furthermore, we provide a fundamental theorem for the optimality of convex quaternion optimization problems, and demonstrate its utility through three applications in quaternion signal processing. These results provide a solid theoretical foundation for convex quaternion optimization and open avenues for further developments in signal processing applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge