Regularize implicit neural representation by itself
Paper and Code
Mar 27, 2023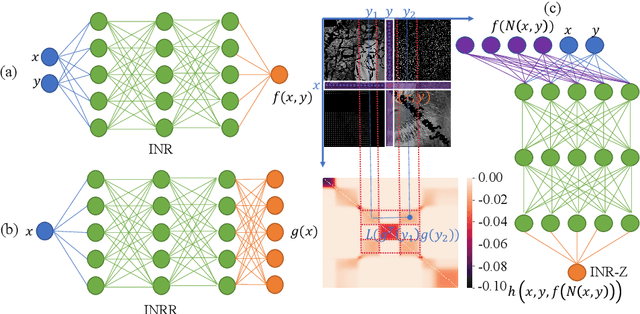
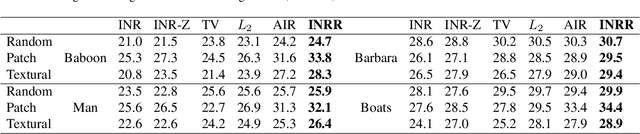


This paper proposes a regularizer called Implicit Neural Representation Regularizer (INRR) to improve the generalization ability of the Implicit Neural Representation (INR). The INR is a fully connected network that can represent signals with details not restricted by grid resolution. However, its generalization ability could be improved, especially with non-uniformly sampled data. The proposed INRR is based on learned Dirichlet Energy (DE) that measures similarities between rows/columns of the matrix. The smoothness of the Laplacian matrix is further integrated by parameterizing DE with a tiny INR. INRR improves the generalization of INR in signal representation by perfectly integrating the signal's self-similarity with the smoothness of the Laplacian matrix. Through well-designed numerical experiments, the paper also reveals a series of properties derived from INRR, including momentum methods like convergence trajectory and multi-scale similarity. Moreover, the proposed method could improve the performance of other signal representation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge