AIR-Net: Adaptive and Implicit Regularization Neural Network for Matrix Completion
Paper and Code
Oct 12, 2021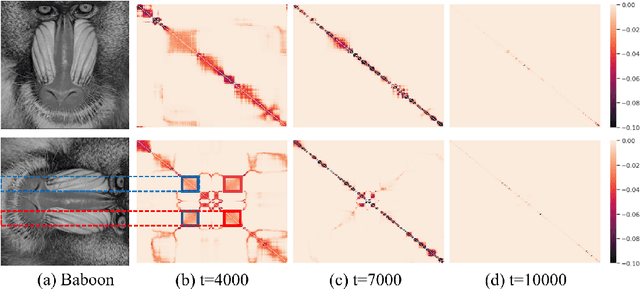
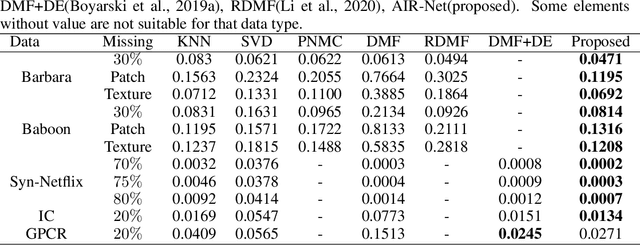
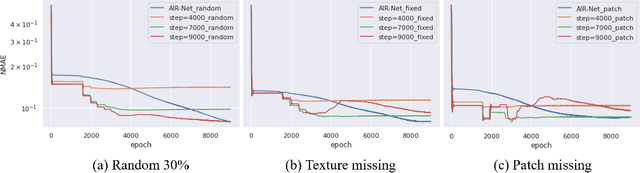
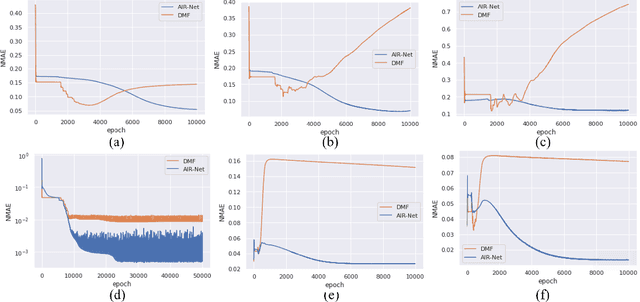
Conventionally, the matrix completion (MC) model aims to recover a matrix from partially observed elements. Accurate recovery necessarily requires a regularization encoding priors of the unknown matrix/signal properly. However, encoding the priors accurately for the complex natural signal is difficult, and even then, the model might not generalize well outside the particular matrix type. This work combines adaptive and implicit low-rank regularization that captures the prior dynamically according to the current recovered matrix. Furthermore, we aim to answer the question: how does adaptive regularization affect implicit regularization? We utilize neural networks to represent Adaptive and Implicit Regularization and named the proposed model \textit{AIR-Net}. Theoretical analyses show that the adaptive part of the AIR-Net enhances implicit regularization. In addition, the adaptive regularizer vanishes at the end, thus can avoid saturation issues. Numerical experiments for various data demonstrate the effectiveness of AIR-Net, especially when the locations of missing elements are not randomly chosen. With complete flexibility to select neural networks for matrix representation, AIR-Net can be extended to solve more general inverse problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge