A Unified Plug-and-Play Algorithm with Projected Landweber Operator for Split Convex Feasibility Problems

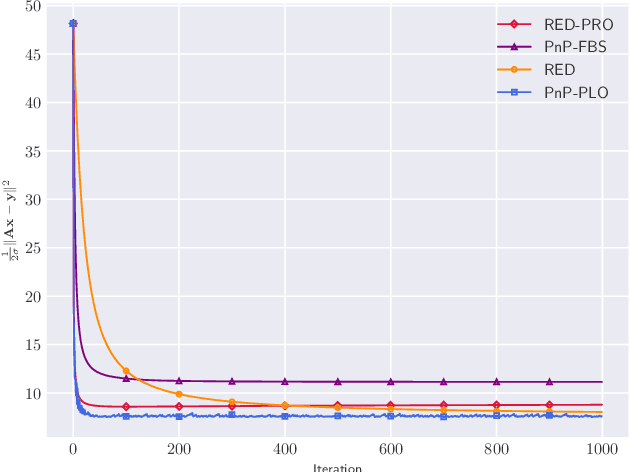
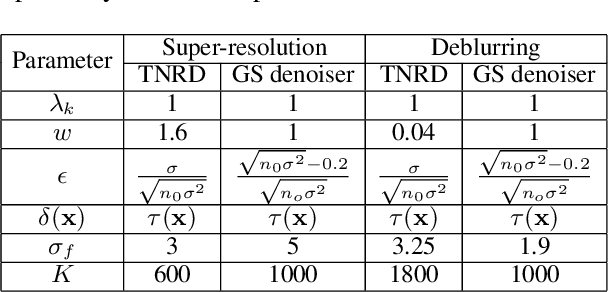
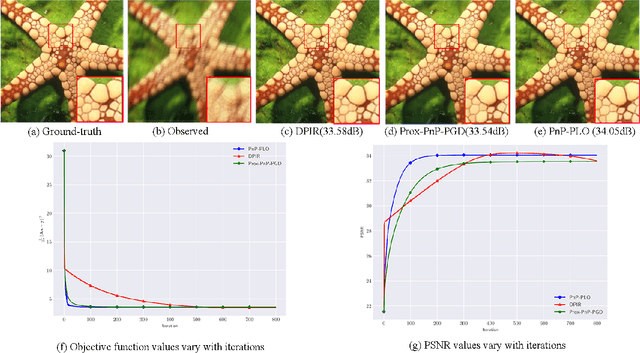
In recent years Plug-and-Play (PnP) methods have achieved state-of-the-art performance in inverse imaging problems by replacing proximal operators with denoisers. Based on the proximal gradient method, some theoretical results of PnP have appeared, where appropriate step size is crucial for convergence analysis. However, in practical applications, applying PnP methods with theoretically guaranteed step sizes is difficult, and these algorithms are limited to Gaussian noise. In this paper,from a perspective of split convex feasibility problems (SCFP), an adaptive PnP algorithm with Projected Landweber Operator (PnP-PLO) is proposed to address these issues. Numerical experiments on image deblurring, super-resolution, and compressed sensing MRI experiments illustrate that PnP-PLO with theoretical guarantees outperforms state-of-the-art methods such as RED and RED-PRO.

HPPP: Halpern-type Preconditioned Proximal Point Algorithms and Applications to Image Restoration

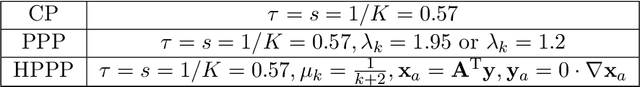
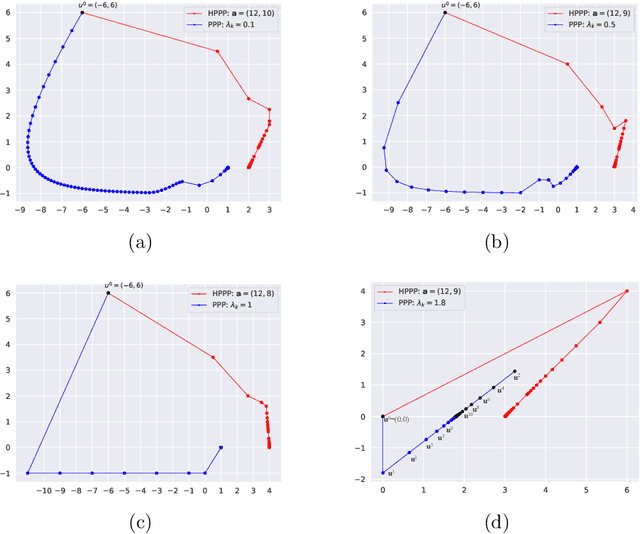
Preconditioned Proximal Point (PPP) algorithms provide a unified framework for splitting methods in image restoration. Recent advancements with RED (Regularization by Denoising) and PnP (Plug-and-Play) priors have achieved state-of-the-art performance in this domain, emphasizing the need for a meaningful particular solution. However, degenerate PPP algorithms typically exhibit weak convergence in infinite-dimensional Hilbert space, leading to uncertain solutions. To address this issue, we propose the Halpern-type Preconditioned Proximal Point (HPPP) algorithm, which leverages the strong convergence properties of Halpern iteration to achieve a particular solution. Based on the implicit regularization defined by gradient RED, we further introduce the Gradient REgularization by Denoising via HPPP called GraRED-HP3 algorithm. The HPPP algorithm is shown to have the regularity converging to a particular solution by a toy example. Additionally, experiments in image deblurring and inpainting validate the effectiveness of GraRED-HP3, showing it surpasses classical methods such as Chambolle-Pock (CP), PPP, RED, and RED-PRO.

A Novel Learning Algorithm for Bayesian Network and Its Efficient Implementation on GPU

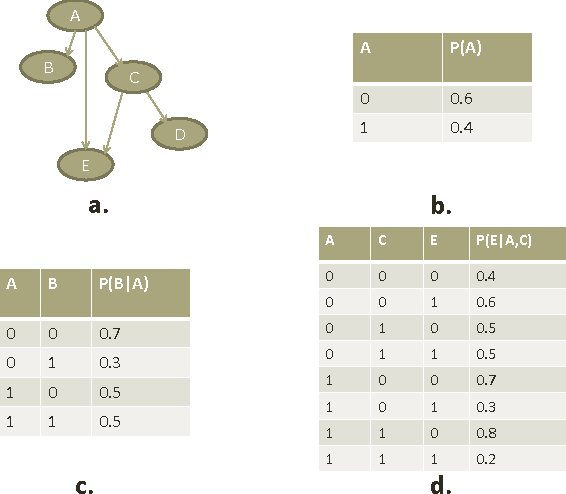
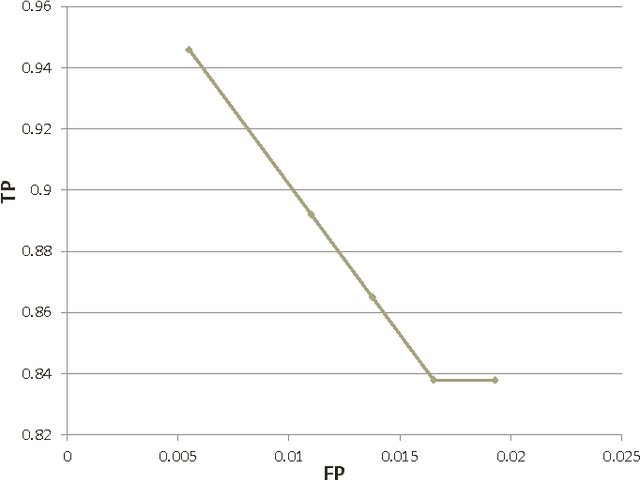
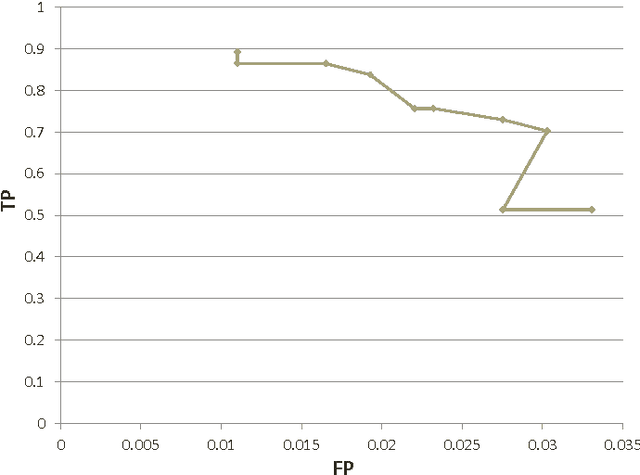
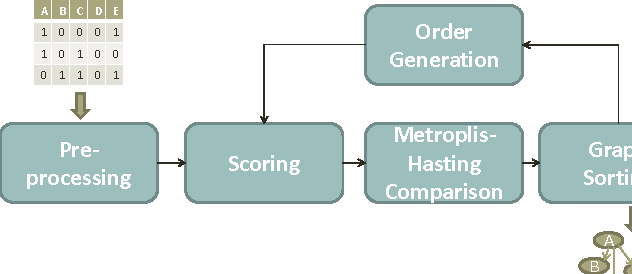
Computational inference of causal relationships underlying complex networks, such as gene-regulatory pathways, is NP-complete due to its combinatorial nature when permuting all possible interactions. Markov chain Monte Carlo (MCMC) has been introduced to sample only part of the combinations while still guaranteeing convergence and traversability, which therefore becomes widely used. However, MCMC is not able to perform efficiently enough for networks that have more than 15~20 nodes because of the computational complexity. In this paper, we use general purpose processor (GPP) and general purpose graphics processing unit (GPGPU) to implement and accelerate a novel Bayesian network learning algorithm. With a hash-table-based memory-saving strategy and a novel task assigning strategy, we achieve a 10-fold acceleration per iteration than using a serial GPP. Specially, we use a greedy method to search for the best graph from a given order. We incorporate a prior component in the current scoring function, which further facilitates the searching. Overall, we are able to apply this system to networks with more than 60 nodes, allowing inferences and modeling of bigger and more complex networks than current methods.