Huanshui Zhang
OCP-LS: An Efficient Algorithm for Visual Localization
Dec 31, 2025Abstract:This paper proposes a novel second-order optimization algorithm. It aims to address large-scale optimization problems in deep learning because it incorporates the OCP method and appropriately approximating the diagonal elements of the Hessian matrix. Extensive experiments on multiple standard visual localization benchmarks demonstrate the significant superiority of the proposed method. Compared with conventional optimiza tion algorithms, our framework achieves competitive localization accuracy while exhibiting faster convergence, enhanced training stability, and improved robustness to noise interference.
A novel algorithm for optimizing bundle adjustment in image sequence alignment
Nov 10, 2024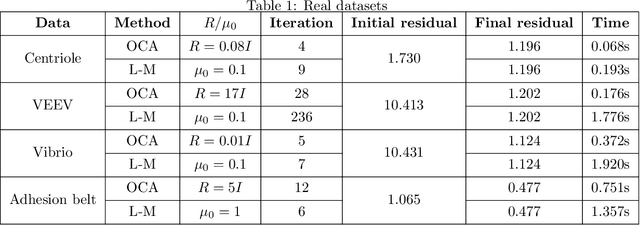
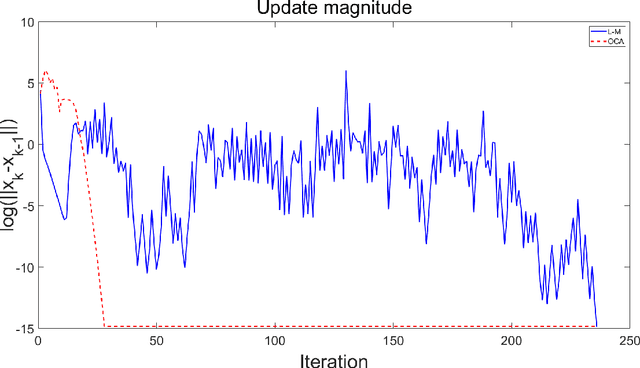
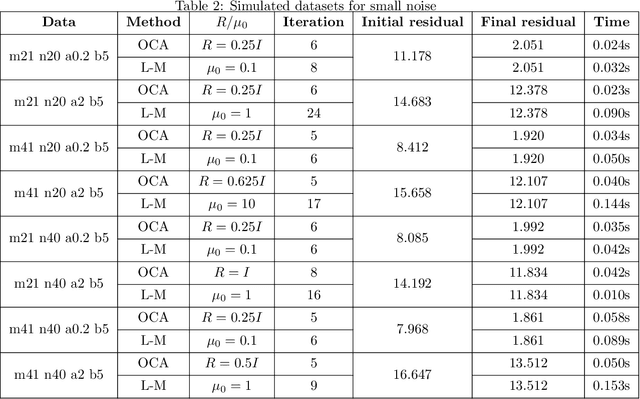
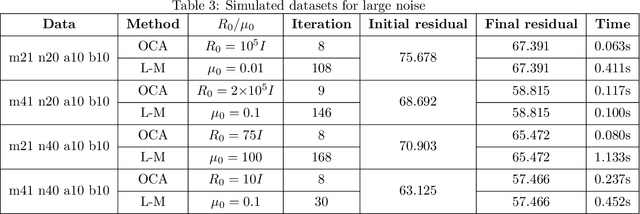
Abstract:The Bundle Adjustment (BA) model is commonly optimized using a nonlinear least squares method, with the Levenberg-Marquardt (L-M) algorithm being a typical choice. However, despite the L-M algorithm's effectiveness, its sensitivity to initial conditions often results in slower convergence when applied to poorly conditioned datasets, motivating the exploration of alternative optimization strategies. This paper introduces a novel algorithm for optimizing the BA model in the context of image sequence alignment for cryo-electron tomography, utilizing optimal control theory to directly optimize general nonlinear functions. The proposed Optimal Control Algorithm (OCA) exhibits superior convergence rates and effectively mitigates the oscillatory behavior frequently observed in L-M algorithm. Extensive experiments on both synthetic and real-world datasets were conducted to evaluate the algorithm's performance. The results demonstrate that the OCA achieves faster convergence compared to the L-M algorithm. Moreover, the incorporation of a bisection-based update procedure significantly enhances the OCA's performance, particularly in poorly initialized datasets. These findings indicate that the OCA can substantially improve the efficiency of 3D reconstructions in cryo-electron tomography.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge