How Does Momentum Benefit Deep Neural Networks Architecture Design? A Few Case Studies
Paper and Code
Oct 19, 2021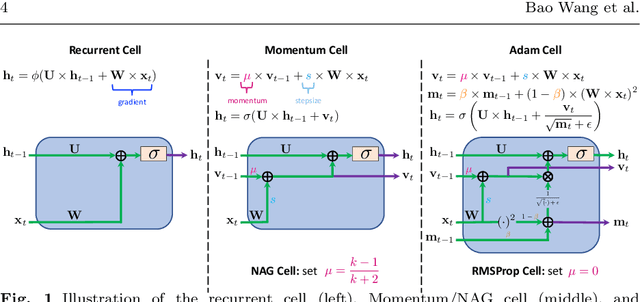
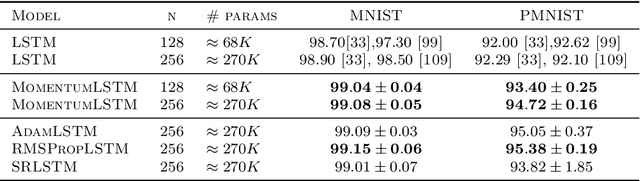

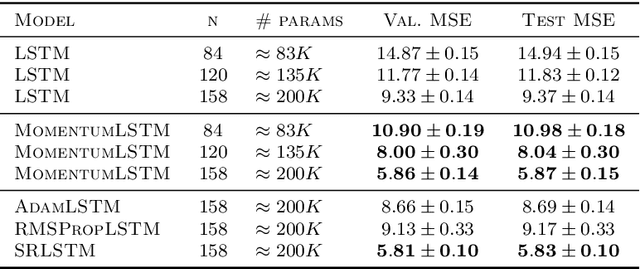
We present and review an algorithmic and theoretical framework for improving neural network architecture design via momentum. As case studies, we consider how momentum can improve the architecture design for recurrent neural networks (RNNs), neural ordinary differential equations (ODEs), and transformers. We show that integrating momentum into neural network architectures has several remarkable theoretical and empirical benefits, including 1) integrating momentum into RNNs and neural ODEs can overcome the vanishing gradient issues in training RNNs and neural ODEs, resulting in effective learning long-term dependencies. 2) momentum in neural ODEs can reduce the stiffness of the ODE dynamics, which significantly enhances the computational efficiency in training and testing. 3) momentum can improve the efficiency and accuracy of transformers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge