Periodic Graph Transformers for Crystal Material Property Prediction
Paper and Code
Sep 23, 2022

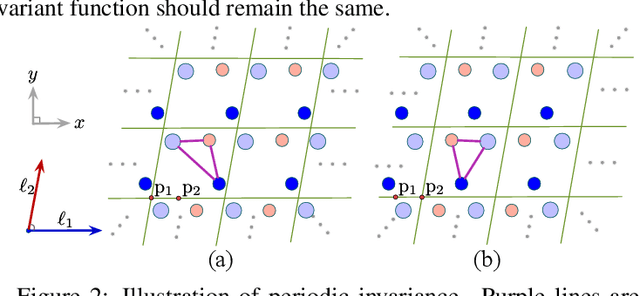
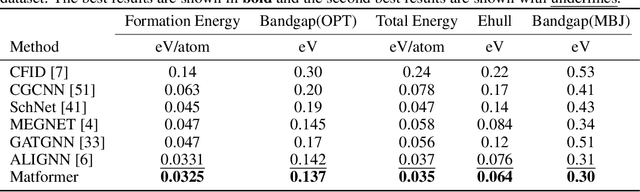
We consider representation learning on periodic graphs encoding crystal materials. Different from regular graphs, periodic graphs consist of a minimum unit cell repeating itself on a regular lattice in 3D space. How to effectively encode these periodic structures poses unique challenges not present in regular graph representation learning. In addition to being E(3) invariant, periodic graph representations need to be periodic invariant. That is, the learned representations should be invariant to shifts of cell boundaries as they are artificially imposed. Furthermore, the periodic repeating patterns need to be captured explicitly as lattices of different sizes and orientations may correspond to different materials. In this work, we propose a transformer architecture, known as Matformer, for periodic graph representation learning. Our Matformer is designed to be invariant to periodicity and can capture repeating patterns explicitly. In particular, Matformer encodes periodic patterns by efficient use of geometric distances between the same atoms in neighboring cells. Experimental results on multiple common benchmark datasets show that our Matformer outperforms baseline methods consistently. In addition, our results demonstrate the importance of periodic invariance and explicit repeating pattern encoding for crystal representation learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge